Быстрый поиск

Реферат: Распределенные алгоритмы

var wsp : boolean init false ;

wrp : integer init 0 ;

recp[q] : boolean для всех q Î Neighp init false ;

vp : P init p ;

statep : (sleep, leader, lost) init sleep ;

begin if p - инициатор then

begin wsp := true ;

forall q Î Neighp do send <wakeup> to q

end ;

while wrp < # Neighp do

begin receive <wakeup> ; wrp := wrp + 1 ;

if not wsp then

begin wsp := true ;

forall q Î Neighp do send <wakeup> to q

end

end ;

(* Начало древовидного алгоритма *)

while # {q : Ørecp[q]} > 1 do

begin receive <tok,r> from q ; recp[q] := true ;

vp := min (vp,r)

end ;

send <tok,vp> to q0 with Ørecp[q0] ;

receive <tok,r> from q0 ;

vp := min (vp,r) ; (* decide с ответом vp *)

if vp = p then statep := leader else statep := lost ;

forall q Î Neighp, q ¹ q0 do send <tok,vp> to q

end

Алгоритм 7.1 Алгоритм выборов для деревьев.

Теорема 7.2 Алгоритм 7.1 решает задачу выбора на деревьях, используя O(N) сообщений и O(D) единиц времени.

Доказательство. Когда хотя бы один процесс инициирует выполнение алгоритма, все процессы посылают сообщения <wakeup> всем своим соседям, и каждый процесс начинает выполнение древовидного алгоритма после получения сообщения <wakeup> от каждого соседа. Все процессы завершают древовидный алгоритм с одним и тем же значением v, а именно, наименьшим идентификатором процесса. Единственный процесс с этим идентификатором закончит выполнение в состоянии лидер, а все остальные процессы - в состоянии проигравший.

Через каждый канал пересылается по два сообщения <wakeup> и по два сообщения <tok,r>, откуда сложность сообщений равна 4N-4. В течение D единиц времени после того, как первый процесс начал алгоритм, каждый процесс послал сообщения <wakeup>, следовательно, в течение D+1 единиц времени каждый процесс начал волну. Легко заметить, что первое решение принимается не позднее, чем через D единиц времени после начала волны, а последнее решение принимается не позднее D единиц времени после первого, откуда полное время равно 3D+1. Более тщательный анализ показывает, что алгоритм всегда завершается за 2D единиц времени, но доказательство этого оставлено читателю; см. Упражнение 7.2.

Если порядок сообщений в канале может быть изменен (т.е. канал - не FIFO), процесс может получить сообщение <tok,r> от соседа прежде чем он получил сообщение <wakeup> от этого соседа. В этом случае сообщение <tok,r> может быть временно сохранено или обработано как сообщения <tok,r>, прибывающие позднее.

Количество сообщений может быть уменьшено с помощью двух модификаций. Во-первых, можно устроить так, чтобы не-инициатор не посылал сообщение <wakeup> процессу, от которого он получил первое сообщение <wakeup>. Во-вторых, сообщение <wakeup>, посылаемое листом, может быть объединено с сообщением <tok,r>, посылаемым этим листом. С этими изменениями количество сообщений, требуемое алгоритмом, уменьшается до 3N-4+k, где k - количество нелистовых стартеров [Tel91b, с.139].

Выбор с помощью фазового алгоритма. Фазовый алгоритм можно использовать для выбора, позволив ему вычислять наименьший идентификатор за одну волну, как в Теореме 6.12.

Теорема 7.3 С помощью фазового алгоритма (Алгоритм 6.7) можно провести выбор в произвольных сетях, используя O(D*|E|) сообщений и O(D) единиц времени.

Алгоритм Пелега [Peleg; Pel90] основан на фазовом алгоритме; он использует O(D*|E|) сообщений и O(D) времени, но не требует знания D, т.к. включает в себя вычисление диаметра.

Выбор с помощью алгоритма Финна. Алгоритм Финна (Алгоритм 6.9) не требует, чтобы диаметр сети был известен заранее. Длина O(N*|E|) сообщений, используемых в алгоритме Финна, гораздо больше, чем допускаемая предположениями в этой главе. Следовательно, каждое сообщение в алгоритме Финна должно считаться за O(N) сообщений, откуда сложность сообщений составляет O(N2|E|).

7.2 Кольцевые сети

В этом разделе рассматриваются некоторые алгоритмы выбора для однонаправленных колец. Задача выбора в контексте кольцевых сетей была впервые изложена ЛеЛанном [LeLann; LeL77], который также дал решение со сложностью сообщений O(N2). Это решение было улучшено Чангом (Chang) и Робертсом (Roberts) [CR79], которые привели алгоритм с наихудшей сложностью O(N2), но со средней сложностью только O(N logN). Решения ЛеЛанна и Чанга-Робертса обсуждаются в Подразделе 7.2.1. Вопрос о существовании алгоритма с наихудшей сложностью O(N logN) оставался открытым до 1980 г., когда такой алгоритм был приведен Hirschberg и Sinclair [HS80]. В отличие от более ранних решений, в решении Hirschberg-Sinclair требуется, чтобы каналы были двунаправленными. Предполагалось, что нижняя граница для однонаправленных колец равна W(N2), но Petersen [Pet82] и Dolev, Klawe и Rodeh [DKR82] независимо друг от друга предложили решение, составляющее O(N log N) для однонаправленного кольца. Это решение рассматривается в Подразделе 7.2.2.

Алгоритмы были дополнены соответствующими нижними границами примерно в то же время. Нижняя граница для наихудшего случая для двунаправленных колец, равная » 0.34N logN сообщений, была доказана Бодлендером [Bodlaender; Bod88]. Pachl, Korach и Rotem [PKR84] доказали нижние границы в W(N logN) для средней сложности, как для двунаправленных так и для однонаправленных колец. Их результаты по нижним границам будут рассмотрены в Подразделе 7.2.3.

7.2.1 Алгоритмы ЛеЛанна и Чанга-Робертса

В алгоритме ЛеЛанна [LeL77] каждый инициатор вычисляет список идентификаторов всех инициаторов, после чего выбирается инициатор с наименьшим идентификатором. Каждый инициатор посылает маркер, содержащий его идентификатор, по кольцу, и этот маркер передается всеми процессами. Предполагается, что каналы подчиняются дисциплине FIFO, и что инициатор должен сгенерировать свой маркер до того, как он получит маркер другого инициатора. (Когда процесс получает маркер, он после этого не инициирует алгоритм.) Когда инициатор p получает свой собственный маркер, маркеры всех инициаторов прошли через p, и p выбирается лишь в том случае, если p - наименьший среди инициаторов; см. Алгоритм 7.2.

var Listp : set of P init {p} ;

statep ;

begin if p - инициатор then

begin statep := cand ; send <tok,p> to Nextp ; receive <tok,q> ;

while q ¹ p do

begin Listp := Listp È {q} ;

send <tok,q> to Nextp ; receive <tok,q> ;

end ;

if p = min (Listp) then statep := leader

else statep := lost

end

else repeat receive <tok,q> ; send <tok,q> to Nextp ;

if statep = sleep then statep := lost

until false

end

Алгоритм 7.2 Алгоритм выбора ЛеЛанна.

Теорема 7.4 Алгоритм ЛеЛанна (Алгоритм 7.2) решает задачу выбора для колец, используя O(N2) сообщений и O(N) единиц времени.

Доказательство. Так как порядок маркеров в кольце сохраняется (из предположения о каналах FIFO), и инициатор q отправляет <tok,q> до того как получит <tok,p>, то инициатор p получает <tok,q> прежде, чем вернется <tok,p>. Отсюда следует, что каждый инициатор p заканчивается со списком Listp, совпадающим с множеством всех инициаторов, и единственным выбираемым процессом становится инициатор с наименьшим идентификатором. Всего получается не больше N маркеров и каждый делает N шагов, что приводит к сложности сообщений в O(N2). Не позднее чем через N-1 единицу времени после того, как первый инициатор отправил свой маркер, это сделали все инициаторы. Каждый инициатор получает свой маркер обратно не позднее, чем через N единиц времени с момента генерации этого маркера. Отсюда следует, что алгоритм завершается в течение 2N-1 единиц времени.

Все не-инициаторы приходят в состояние проигравший, но навсегда остаются в ожидании сообщений <tok,r>. Ожидание может быть прервано, если лидер посылает по кольцу специальный маркер, чтобы объявить об окончании выбора.

Алгоритм Чанга-Робертса [CR79] улучшает алгоритм ЛеЛанна, устраняя из кольца маркеры тех процессов, для которых очевидно, что они проиграют выборы. Т.е. инициатор p удаляет из кольца маркер <tok,q>, если q > p. Инициатор p становится проигравшим, когда получает маркер с идентификатором q < p, или лидером, когда он получает маркер с идентификатором p; см. Алгоритм 7.3.

var statep ;

begin if p - инициатор then

begin statep := cand ; send <tok,p> to Nextp ;

repeat receive <tok,q> ;

if q = p then statep := leader

else if q < p then

begin if statep = cand then statep := lost ;

send <tok,q> to Nextp

end

until statep = leader

end

else repeat receive <tok,q> ; send <tok,q> to Nextp ;

if statep = sleep then statep := lost

until false

end

(* Только лидер завершает выполнение программы. Он передает сообщение всем процессам, чтобы сообщить им идентификатор лидера и завершить их *)

Алгоритм 7.3 Алгоритм выбора Чанга-Робертса.

Теорема 7.5 Алгоритм Чанга-Робертса (Алгоритм 7.3) решает задачу выбора для колец, используя Q(N2) сообщений в наихудшем случае и O(N) единиц времени.

Доказательство. Пусть p0 - инициатор с наименьшим идентификатором. Все процессы являются либо не-инициаторами, либо инициаторами с идентификаторами большими p0, поэтому все процессы передают дальше маркер <tok,p0>, отправленный p0. Следовательно, p0 получает свой маркер обратно и становится выбранным.

Не-инициаторы не могут быть выбраны, т.к. все они приходят в состояние проигравший самое позднее, когда через них передается маркер p0. Инициатор p с p > p0 не может быть выбран; p0 не передаст дальше маркер <tok,p>, поэтому p никогда не получит свой собственный маркер. Такой инициатор p приходит в состояние проигравший самое позднее, когда через него передается маркер <tok,p0>. Таким образом доказано, что алгоритм решает задачу выбора.

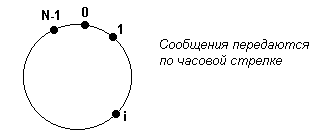
Рис.7.4 Наихудший случай для алгоритма Чанга-Робертса.

Всего используется не более N различных маркеров и каждый маркер делает не более N переходов, что подтверждает границу сложности сообщений O(N2). Чтобы показать, что в самом деле можно использовать W(N2) сообщений, рассмотрим начальную конфигурацию, где все идентификаторы расположены в возрастающем порядке вдоль кольца (см. Рис. 7.4) и каждый процесс является инициатором. Маркер каждого процесса удаляется из кольца процессом 0, таким образом маркер процесса i совершает N-i переходов, откуда следует, что количество пересылок сообщений равно .

Алгоритм Чанга-Робертса не улучшает алгоритм ЛеЛанна в отношении временной сложности или наихудшего случая сложности сообщений. Улучшение касается только среднего случая, где усреднение ведется по всевозможным расположениям идентификаторов вдоль кольца.

Теорема 7.6 Алгоритм Чанга-Робертса в среднем случае, когда все процессы являются инициаторами, требует только O(N logN) пересылок сообщений.

Доказательство. (Это доказательство основано на предложении Friedemann Mattern.)

Предположив, что все процессы являются инициаторами, вычислим среднее количество пересылок маркера по всем круговым расположениям N различных идентификаторов. Рассмотрим фиксированное множество из N идентификаторов, и пусть s будет наименьшим идентификатором. Существует (N-1)! различных круговых расположений идентификаторов; в данном круговом расположении пусть pi - идентификатор, находящийся за i шагов до s; см. Рис. 7.5.

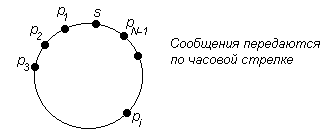
Рис.7.5 Расположение идентификаторов на кольце.

Чтобы вычислить суммарное количество пересылок маркера по всем расположениям, вычислим сначала суммарное количество пересылок маркера <tok,pi> по всем расположениям, а потом просуммируем по i. Маркер <tok,s> при любом расположении передается N раз, следовательно, он пересылается всего N(N-1)! раз. Маркер <tok,pi> передается не более i раз, так как он будет удален из кольца, если достигнет s. Пусть Ai,k - количество циклических расположений, при которых <tok,pi> передается ровно k раз. Тогда суммарное число пересылок <tok,pi> равно .

Маркер <tok,pi> передается ровно i раз, если pi является наименьшим из идентификаторов от p1 до pi, что имеет место в (1/i)*(N-1)! расположениях; итак

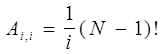
Маркер <tok,pi> передается не менее k раз (здесь k £ i), если за процессом pi следует k-1 процесс с идентификаторами, большими pi. Количество расположений, в которых pi - наименьший из k идентификаторов pi-k+1, ..., pi, составляет 1/k часть всех расположений, т.е. (1/k)*(N-1)!. Теперь, для k<i <tok,pi> передается ровно k раз, если он передается не менее, но и не более k раз, т.е. ³ k раз, но не ³ k+1 раз. В результате количество расположений, где это выполняется, равно , т.е. ( для k < i ).