Быстрый поиск

Реферат: Распределенные алгоритмы

Рисунок 4.15 Интервальная разметка поиском в глубину.

Лемма 4.28 Если lu > lv то lw < Iu

Доказательство. Во-первых, рассмотрим случай auw £ lv. Узел w не сын u потому что в этом случае auw = lw > lu > lv .Если uw ветвь то также lw = auw < lv < lu. Если w отец u то lw < lu выполняется в любом случае. Во-вторых, рассмотрим случай когда auw – наибольшая метка ребра в u, и нет метки a' £ lv (т.е., lv – нижняя граница нелинейного интервала). В этом случае ребро к отцу u не помечено 0, но имеет метку ku (потому что 0£ lv, и нет метки a' £ lv). Метка ku – наибольшая метка в данном случае; ребро к сыну или ветви вниз w' имеет auw’ = lw’ < ku, и ветвь к предком w' имеет auw’ = lw’ < lu Таким образом w – отец u в данном случае, что подразумевает 1w < lu. []

Следующие две леммы относятся к случаю когда lu < lv. Мы выведем что каждый v Î T[u] или lv > ku, и в последнем случае ku < N имеет силу так что ребро к отцу u помечено ku.

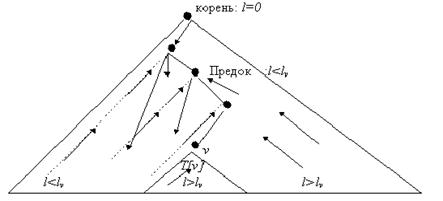
Рисунок 4.16 МАРШРУТИЗАЦИЯ ПАКЕТОВ ДЛЯ V В СХЕМЕ РАЗМЕТКИ ILS.

Лемма 4.29 Если lu <lv то lw £ lv.

Доказательство. Во-первых, рассмотрим случай когда v Î T[u]; пусть w' сын u такой что vÎT[w’]. Мы имеем auw’ = lw' £ lv и это подразумевает что auw’ £auw£lv < kw’. Мы вывели что w не является отцом u, следовательно 1w = auw, что подразумевает lw < lv.

Во-вторых, рассмотрим случай когда lv ³ ku. В этом случае w отец u, это можно показать следующим образом. Ребро к отцу помечено ku, и ku £ lv. Ребро к сыну w' узла u помечено 1w’ < ku , ребро к ветви вниз w' помечено 1w’ <ku, и ребро ветви вверх w' помечено 1w’ < lu. Поэтому w отец u, lw < lu < lv. []

Нормфункция относящаяся к передаче в v может быть определена следующим образом. Наименьший общий предок двух узлов u и v это наименьший узел в дереве который отец u и v. Пусть lca(u, v) означает метку наименьшего общего предка u и v, и определим

fv(u) = (-lca(u, v), 1u).

Лемма 4.30 Если lu < lv то fv(w) < fv(u).

Доказательство. Во-первых рассмотрим случай когда v ÎT[u], что подразумевает lca(u, v) = lu. Если w' сын u такой что v Î T[w’], мы имеем (как в предыдущей Лемме) что 1w’ £ lw < kw’, следовательно w ÎT[w'], что подразумевает lca(u, v) ³ lw’ > lu. Таким образом fv(w) < fv(u).

Во-вторых, рассмотрим случай что 1v > ku. Как в предыдущей лемме, w отец u, и поэтому vÏT[u], lca(w, v)= lca(u, v). Но теперь 1w < lu , таким образом fv(w)< fv(u). []

Может быть показано что каждый пакет достигает пункта назначения. Поток пакетов для v показан на Рисунке 4.16. Пусть пакет для v сгенерирован в узле u. По Лемме 4.28, метка узла уменьшается с каждым переходом, до тех пор пока, за конечное число шагов, пакет получен узлом w с 1w£lv. Каждый узел к которому пакет пересылается после w также имеет метку £lv по лемме 4.29. За конечное число шагов пакет получает v, потому что с каждым шагом fv уменьшается или пакет прибывает в v, по Лемме 4.30. Это завершает доказательство Теоремы 4.25. []

Эффективность интервальной маршрутизации: общий случай. Теорема 4.25 говорит что корректная ILS существует для каждой сети, но не предполагает ничего о эффективности путей выбранных схемой. Ясно что ILS с поиском в глубину используется для демонстрации существования схемы для каждой сети, но что они не обязательно лучшие возможные схемы. На пример, если схема с обходом в глубину применена к кольцу из N узлов, существуют узлы u и v с d(u, v) == 2, и схема использует N — 2 переходов для передачи пакета от u к v (Упражнение 4.8). Существует ILS для того же кольца что которая пересылает каждый пакет через путь с минимальным количеством шагов. (Теорема 4.34).

Определение 4.31 ILS оптимальна если она передает все пакеты через оптимальные пути.

ILS общительна если она передает пакет от одного узла к соседу данного узла за один шаг.

ILS линейна если интервал для передачи в каждом ребре линейный.

Мы называли ILS с минимальным количеством шагов (или кротчайший путь) если она оптимальна относительно оценки пути мерой минимальным количеством шагов (или кратчайший путь, соответственно). Просто показать что если схема удовлетворяет мере минимального количества шагов то схема общительна. Также легко проверить что ILS линейна тогда и только тогда когда в каждом узле u с lu ¹ 0 существует ребро с пометкой 0, и в узле с пометкой 0 существует ребро с меткой 0 или 1. Это показывает что для сетей в общем виде качество методов маршрутизации плохое, но для некоторых классов специальной сетевой топологии качество схемы очень неплохое. Это делает метод процессорных сетей с регулярной структурой, которые используются для реализации параллельных вычислений с виртуальной общей разделяемой памяти.

Не известно точно как, для произвольной сети, лучшие схемы интервальной разметки сравниваются с оптимальными алгоритмами маршрутизации. Некоторые нижние границы длин путей, как подразумевают оптимальные ILS не всегда существуют, было дано Ружечкой(Ruzecka).

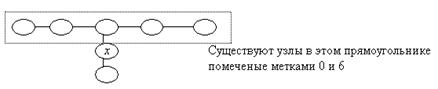
Рисунок 4.1T Граф-паук с тремя ногами

Теорема 4.32 [Ruz88] Существует сеть G такая что для каждой верной ILS в G существуют узлы u и v такие что пакет от u к v доставлен только после по крайней мере 3/2DG переходов.

Известно как лучшие схемы ILC с поиском в глубину сравниваются с общими лучшими схемами ILS для этих же сетей. Упражнение 4.7 дает очень плохую схему ILS с поиском в глубину для сети которая действительно допускает оптимальную ILS (по Теореме 4.37), но может существовать лучшая схема ILS с поиском в глубину для такой сети.

В ситуациях когда большинство соединений происходят ммежду соседями, будучи общительными достаточные требования для ILS. Так можно показать из Рисунка 4.15 схема ILS с поиском в глубину не обязательно общительна; узел 4 передает пакеты для узла 2 через узел 1.

Это существенно для применимости метода интервальной маршрутизации, которым рассматриваются циклические интервалы. Хотя некоторые сети допустимы, и даже оптимальны, схемы с линейноинтервальной маршрутизации, не возможно маркировать каждую сеть линейными интервалами. Применимость схемы линейноинтервальной разметки была исследована Бэккером, Ван Лиуином, и Таном [BLT91].

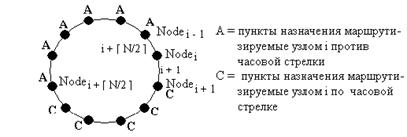
Рисунок 4.18 Оптимальная ILS для кольца

Теорема 4.33 Существует сеть для которой нет применимой схемы линейноинтервальной разметки

Доказательство. Рассмотрим граф-паук с тремя ногами длины 2, как нарисовано на Рисунке 4.17. Наименьшей матка (0) и наибольшей метка (6) означены два узла, и так как всего три ноги, существует(по крайней мере) одна нога которая не содержит ни меньшую ни большую метку. Пусть x будет первым узлом отцентра в этой ноге. Узел x передает пакета адресованные к 0 и 6 в центр, и единственный линейный интервал который содержит и 0 и 6 это полное множество ZN . Следовательно, x также пересылает пакеты для своих соседей через центр, и эти пакеты никогда не достигнут своих пунктов назначения. []

Бэккер, Ван Лиуин и Taн полностью описали класс сетей топологии которых допускают линейные схемы ILS кротчайших путей и представили результаты содержащие классы графических топологий которые допускают адаптацию и линейные схемы ILS с минимальным количеством шагов линейны.

Оптимальность интервальной маршрутизации: специальные топологии.

Было показано что существуют оптимальные схемы интервальной разметки для некоторых классов сетей имеющих регулярную структуру. Сети таких структур используются , например, в реализации параллельных вычислений.

Теорема 4.34 [LT87] Существует схема ILS с минимальным количеством шагов для кольца из N узлов.

Доказательство. Метки узлов означены от 0 до N — I по часовой стрелке. Для узла i канал по часовой стрелке означен меткой i +1 и канал против часовой стрелке означен (i+ [N/2]) mod N, см Рисунок 4.18. С этой схемой разметки узел с меткой i посылает пакеты для узлов i+1, ..., (i+ [N/2] ) -1 через канал по часовой стрелке и пакеты для узлов (i + [N/2]), . . . , i —1 через канал против часовой стрелке, что является оптимальным. []

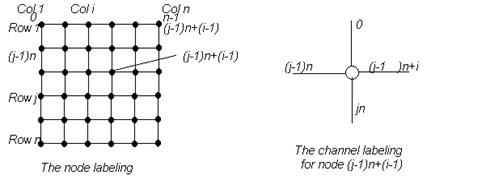
Рисунок 4.19 Оптимальная ILS для сетки n x n.

Так как ILS iв Доказательстве Теоремы 4.34 оптимальна , она общительна; она линейна.

Теорема 4.35 [LT87] Существует схема ILS с минимальным количеством шагов для сетки n x n .

Доказательство. Метки узлов означены по рядам в возрастающем порядке, т.е., i-ый узел в j-ом ряду помечен (j - l)n + (i - 1). Канал вверх этого узла помечен 0, канал налево этого узла помечен (j - l)n, канал направо помечен (J - l)n + i, и канал вниз помечен j n, см Рисунок 4.19. Теперь легко проверить что когда узел u передает пакет к узлу v,

Случай 1: если v в ряду большем чем u, тогда u посылает пакет через свой канал наверх;

Случай 2: если v в ряду меньшем чем u, тогда u посылает пакет через свой канал вниз;

Случай 3: если v в том же ряду что и u но левее, u посылает пакет через свой левый канал; и

Случай 4: если v в том же ряду что и u но правее, то u посылает пакет через свой канал направо.

Во всех случаях , u посылает пакет к узлу ближайшему к v, что и подразумевает что выбранный путь оптимальный. []

Так как ILS в Доказательстве Теоремы 4.35 оптимальна, он общительна; то схема также линейна.

Теорема 4.36 Существует линейная схема ILS с минимальным количеством шагов для гиперкуба.

Теорема 4.37 [FJ88] Существует схема ILS кротчайших путей для непланарных сетей с произвольными весами каналов.

Интервальная маршрутизация имеет некоторые привлекательные преимущества, как следствия, над механизмами классической маршрутизации основанными на хранении привилегированных каналов отдельно для каждого пункта назначения.

(1) Малая пространственная сложность. Таблицы маршрутизации могут хранится в 0(deg • log N) бит для узла степенью deg.

(2) Эффективность вычислений таблиц маршрутизации. Таблицы маршрутизации для схем ILC c поиском в глубину могут быть вычислены используя распределенный обход сети в глубину, который может использовать O(E) сообщений за время 0(N) ; см Часть 6.4.

(3) Оптимальность. Метод маршрутизации способен выбирать оптимальный петь в некоторых классах сетей, см. Теоремы с 4.34 до 4.37.

Эти преимущества делают метод применимым для процессорных сетей с регулярной топологией. Транспьютеры часто используются для конструирования таких топологий, маршрутизационные чипы Инмос 104 (смотри Раздел 1.1.5) разработаны для использования интервальной маршрутизации.

К сожалению, для сетей с произвольной топологией, когда методы используют схемы ILS с поиском в глубину присутствуют несколько минусов:

(1) Плохая живучесть. Не возможна легкая адаптация схемы ILS с поиском в глубину при добавлении или удалении узла в сети. Дерево ILS не может долго удовлетворять требованию по которому ветвь существует только между узлом и его предком. В результате минимальное изменение топологии сети может потребовать полного перевычисления таблиц маршрутизации, включая вычисление новых адресов (меток) для каждого узла.

(2) Не оптимальность. Схема ILS поиска в глубину может направлять пакет через пути длиной W(N), даже в случаях сетей с малым диаметром; см Упражнение 4.7.

(* A пакет с адресом d был получен или создан узлом u *)

if d = lu

then обработать пакет локально

else begin ai := самая ддлинная матка канала т.что ai < d ;

послать пакет через канал помеченый ai

end

Алгоритм 4.20 Префиксная передача (для узла u).

4.4.3 Префиксная маршрутизация

Рассмотрев недостатки интервальной маршрутизации, Бэккер, Ван Лиуин, и Taн [BLT93] разработали метод маршрутизации в котором таблицы могут быть вычислены используя произвольное дерево охвата. Использование неограниченного дерева охвата может увеличить как живучесть так и эффективность. Если a канал добавлен между двумя существующими узлами то дерево охвата остается деревом охвата а новый канал будет ветвью. Если новый узел добавляется вместе с некоторым количеством каналов соединяющих его с существующими узлами то дерево охвата расширяется используя один из каналов и новый узел. Остальные каналы становятся ветвями. Оптимальность может быть улучшена выбором дерева охвата малой глубины (как в лемме 4.22.)

Как метки узлов и каналов в префиксной маршрутизации предпочтительнее использовать строки чем целые числа, используемые в интервальной маршрутизации. Пусть S – алфавит; в последствии метка будет строкой над S, s обозначает пустую строку, и S* множество строк над S. Для отбора канала для передачи пакета, алгоритм рассматривает все каналы которые являются префиксами адреса пункта назначения. Выбирается самая длинная из этих меток, и выбранный канал используется для передачи пакета. На пример, предположим что узел имеет каналы с метками aabb, abba, aab, aabc, и aa, и должен переслать пакет с адресом aabbc. Метки каналов aabb, aab, и aa являются префиксами aabbc, и самая длинная из этих трех меток aabb, следовательно узел передаст пакет через канал помеченный aabb. Алгоритм передачи дан как Алгоритм 4.20. Мы пишем a <b для обозначения что a префикс b.