 Реферат: Распределенные алгоритмы
Реферат: Распределенные алгоритмы
Пусть S будет системой переходов и Р – предикат. Определим term как предикат, который истина во всех терминальных конфигурациях и ложь во всех нетерминальных конфигурациях. Мы сначала предположим ситуации, где исполнение достигает терминальной конфигурации. Обычно нежелательно, чтобы такая конфигурация достигалась, в то время, как «цель» Р не была достигнута. Говорят, что в этом случае имеет место тупик. С другой стороны, завершение позволено, если цель была достигнута, в этом случае говорят о правильном завершении.
Определение 2.14 Система S завершается правильно (или без тупиков), если предикат (term Þ Р) всегда истинен в системе S.
Нормирующие функции полагаются га математическое понятие обоснованных множеств. Это множество с порядком <, где нет бесконечных убывающих последовательностей.
Определение 2.15 Частичный порядок (W, <) является обоснованным, если в нем нет бесконечной убывающей последовательности
w1 > w2 > w3 ... .
Примеры обоснованных множеств, которые будут использоваться в этой книге – это натуральные числа с обычным порядком, и n-кортежи натуральных чисел с лексикографическим порядком (см. раздел 4.3). Свойство, что обоснованное множество не имеет бесконечной убывающей последовательности, может использоваться, чтобы показать, что утверждение Р в конечном счете истина. К этому моменту должно быть показано, что существует функция f из C в обоснованное множество W такая, что в каждом переходе значение f убывает или Р становится истиной.
Определение 2.16 Пусть даны система переходов S и утверждение Р. Функция f из С в обоснованное множество W называется нормирующей функцией (по отношению к Р), если для каждого перехода g à d , f(g) > f(d) или Р(d).
Теорема 2.17 Пусть даны система переходов S и утверждение Р. Если S завершается правильно и нормирующая функция f (w.r.t Р) существует, то Р – истина в некоторой конфигурации каждого исполнения системы S.
Доказательство. Пусть Е = (g0, g1, g3, ...) – исполнение системы S. Если Е конечно, его последняя конфигурация является терминальной, и т.к. term Þ Р всегда истина в системе S, то Р выполняется в этой конфигурации. Если Е бесконечно, пусть E’ будет самым длинным префиксом Е, который не содержит конфигураций, в которых Р истина, и пусть s будет последовательностью (f(g0 ), f(g1), ...) для всех конфигураций gi, которые появляются в Е’. В зависимости от выбора Е’ и свойства f, s может быть убывающей последовательностью, и отсюда, по обоснованности W, s конечна. Это подразумевает также, что Е’ – конечный префикс (g0, g1, ..., gk ) исполнения Е. В зависимости от выбора Е’, Р(gk+1) выполняется.
Если приняты свойства справедливости, то можно заключить из более слабых посылок (чем в теореме 2.17), что Р в конце концов станет истиной. Значение нормирующей функции не должно уменьшаться при каждом переходе. Предположение справедливости может быть использовано, чтобы показать, что бесконечные исполнения содержат переходы определенного типа бесконечно часто. Затем будет достаточно показать, что f никогда не увеличивается, а уменьшается с каждым переходом этого типа.
В некоторых случаях мы будем использовать следующий результат, который есть специальный случай теоремы 2.17
Теорема 2.18 Если S завершается правильно и есть число К такое, что каждое исполнение содержит по крайней мере К переходов, то Р истина в некоторой конфигурации каждого исполнения.
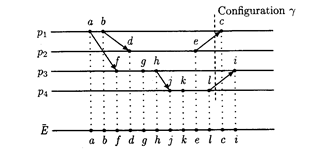
Рис. 2.1 Пример пространственно-временной диаграммы
2.3 Каузальный порядок событий и логические часы
Взгляд на исполнения как последовательности переходов естественным образом порождает понятие времени в исполнениях. Говорят, что переход а появляется раньше перехода b, если a встречается в последовательности перед b. Для исполнения Е = (g0, g1, ...) определим ассоциированную последовательность событий Е’=(е0, е1, ...), где еi – это событие, при котором конфигурация изменяется из gi в gi+1. Заметьте, что каждое исполнение определяет уникальную последовательность событий этим путем. Исполнение может быть визуализировано в пространственно-временной диаграмме, рисунок 2.1, которой, представляет пример. В такой диаграмме, горизонтальная линия нарисована для каждого процесса, и каждое событие нарисовано точкой на линии процесса, где оно имеет место. Если сообщение m послано при событии s и получено при событии r, стрелка рисуется от s к r. Говорят, что события s и r соответственные в этом случае.
Как мы увидим в подразделе 2.3.1, события распределенного исполнения могут иногда быть взаимно обменены без воздействия на последующие конфигурации исполнения. Поэтому понятие времени как абсолютного порядка на событиях исполнения не приемлемо для распределенных исполнений, и вместо этого представляется понятие каузальной зависимости. Эквивалентность исполнений при переупорядочивании событий изучается в подразделе 2.3.2. Мы обсуждаем в подразделе 2.3.3 как могут быть определены часы для измерения каузальной зависимости (а не времени), и представляем логические часы Лампорта, важный пример таких часов.
2.3.1 Независимость и зависимость событий
Уже было замечено, что переходы распределенной системы влияют, и подвержены влиянию, только на часть конфигураций. Это ведет к тому наблюдению, что два последовательных события, влияя на разделенные части конфигурации, независимы и могут также появляться в обратном порядке. Для систем с асинхронной передачей сообщений, это выражается в следующей теореме.
Теорема 2.19 Пусть g будет конфигурацией распределенной системы (с асинхронной передачей сообщений) и пусть ер и еq будут событиями различных процессов р и q, применимых в g. Тогда ер применимо в еq(g), еq применимо в ер(g), и ер(еq(g)) = еq(ер(g)).
Доказательство. Чтобы избежать анализа случаев, которые есть посылка, получение, или внутренние события, мы представим каждое событие однородной нотацией (с, х, у, d). Здесь с и d обозначают состояние процесса до и после события, х – набор сообщений, полученных во время события, и у – набор сообщений, посланных во течение события. Таким образом, внутренне событие (с, d) обозначается как (c,Æ,Æ,d), событие отправки (с, m, d) обозначается как (с, Æ, {m}, d), и событие приема (с, m, d) – (c, {m}, Æ, d). В этой нотации, событие е = (с, x, y, d) процесса p применимо в конфигурации g = (Сp1, ..., Cp, ..., СрN, M), если ср = с и x Í M. В этом случае
е(g) = (Сp1, ..., d, ..., (M \ x) È у).
Теперь предположим ер = (bp, xр, ур, dp) и еq = (bq, xq, уq, dq) применимы в
g = (..., ср, ..., сq, ..., M),
то есть ср = bp, cq = bq, xp
Í M, и xq Í M. Важное наблюдение состоит в том,
что хр и xq разделены, сообщение в xp (если
есть такое) имеет назначением р, в то время как сообщение в хq (если
есть такое) имеет назначением q.
Запишем gр = ер(g), и запомним что
gр = (..., dp, ..., cq, ..., (M \ xp ) È ур ).
Так как xq Í M и xq Ç хр = Æ, следует, что хq Í (M \ xp È ур ), и отсюда еq применимо в gр. Запишем gpq = eq(gр), и запомним, что
gрq = (..., dp, ..., dq, ..., ((M \ xp È ур ) \ xq ) È уq ).
С помощью симметричного аргумента может быть показано, что ер применимо в gq = eq(g). Запишем gqp = ep(gq), и запомним, что
gqp = (..., dp, ..., dq, ..., ((M \ xq È уq ) \ xp ) È уp ).
Так как M – мультимножество сообщений, xp Í M, и xq Í M,
((M \ xp È ур ) \ хq È уq ) = ((M \ xq È уq ) \ xp È ур ),
и отсюда gpq = gqp .
Пусть ер и еq будут двумя событиями, которые появляются последовательно в исполнении, т.е. исполнение содержит подпоследовательность
..., g, ер(g), еq(ер(g)), ...
для некоторых g. Посылка теоремы 2.19
применима к этим событиям за исключением следующих двух случаев.
(1) p = q; или
(2) ер – событие отправки, и еq - соответствующее событие получения.
В самом деле, теорема явно утверждает, что p и q должны быть различными, и если еq получает сообщение, посланное в ер, событие отправки не применимо в начальной конфигурации события ep, как требуется. Таким образом, если одно из этих двух утверждений истина, события не могут появляться в обратном порядке, иначе они могут встречаться в обратном порядке и кроме того иметь результат в одной конфигурации. Запомните, что с глобальной точки зрения переходы не могут быть обменены, потому что (в нотации теоремы 2.19) переход из gр в gpq отличается от перехода из g в gq. Однако, с точки зрения процесса эти события неразличимы.
Тот факт, что конкретная пара событий не может быть обменена, выражается тем, что существует каузальное отношение между этими двумя событиями. Это отношение может быть расширено до частичного порядка на множестве событий в исполнении, называемого каузальный порядок исполнения.
Определение 2.20 Пусть Е – исполнение. Отношение í, называемое каузальным порядком, на событиях исполнения есть самое малое отношение, которое удовлетворяет
(1) Если е и f – различные события одного процесса и е появляется перед f, то е í f.
(2) Если s – событие отправки и r – соответствующее событие получения, то s í r.
(3) Отношение í транзитивно.
Мы пишем а í= b, чтобы обозначить (а í b Ú а = b). Так как í= есть частичный порядок, могут существовать события а и b, для которых ни а í= b ни b í= а не выполняется. Говорят такие события конкурирующие, в нотации а || b. На рисунке 2.1, b || f, d || i, и т.д.
Каузальный порядок был впервые определен Лампортом [Lam78] и играет важную роль в рассуждениях, относящихся к распределенным алгоритмам. Определение í подразумевает существование каузальной цепочки между каузально связанными событиями. Этим мы подразумеваем, что а í b включает существование последовательности а = е0 , е1 , ..., ек = b такой, что каждая пара последовательных событий в цепочке удовлетворяет либо (1), либо (2) в определении 2.20. Каузальная цепочка может быть даже выбрана так, что каждая пара, удовлетворяющая (1), есть последовательная пара событий в процессе, где они встречаются, т.е., нет событий между ними. На рисунке 2.1 каузальная цепочка между событием а и событием l есть последовательность а, f, g, h, j, k, l.
2.3.2 Эквивалентность исполнений: вычисления
В этом подразделе показывается, что события исполнения могут быть переупорядочены в любом порядке, согласующимся с каузальным порядком, без воздействия на результат исполнения. Это переупорядочивание событий вызывает другую последовательность конфигураций, но это исполнение будет рассматриваться как эквивалент исходного исполнения.
Пусть f = (f0 , f1 , f2 ,...) будет последовательностью событий. Эта последовательность - последовательность событий относящихся к исполнению F = (d0, d1, d2, ...), если для каждого i, fi применимо в di и fi (di) = di+1. В этом случае F называется включенным исполнением последовательности f. Мы хотели бы, чтобы F уникально определялась последовательностью f, но это не всегда так. Если для некоторого процесса p нет события в p, включенного в f, то состояние процесса p может быть произвольным начальным состоянием. Однако, если f содержит по крайней мере одно событие из р, то первое событие в р, скажем (с, х, у, d), определяет, что начальное состояние процесса р будет с. Поэтому, если f содержит по крайней мере одно событие в каждом процессе, d0 уникально определено, и это определяет целое исполнение уникально.
Теперь пусть Е = (g0, g1, g2, ... ) будет исполнением с ассоциированной последовательностью событий Е’ = (е0 , е1 , е2 , ...) и положим, что f –перестановка из Е’. Это означает, что существует перестановка s натуральных чисел (или множества {0, ..., k-1}, если Е – конечное исполнение с k событиями) таких, что fi = еs(i). Перестановка (f0 , f1 , f2 , ...) событий из Е согласующаяся с каузальным порядком, если fi í= fj подразумевает i £ j, т.е., если нет события, которому предшествует в последовательности событие, которому оно само каузально предшествует.
Теорема 2.21 Пусть f = (f0 , f1 , f2 , ...) – перестановка событий из Е, которая согласуется с каузальным порядком исполнения Е. Тогда f определяет уникальное исполнение F, начинающееся в начальной конфигурации из Е. F имеет столько же событий сколько и Е, и если Е конечно, то последняя конфигурация из F такая же как и последняя конфигурация из Е.
Доказательство. Конфигурации из F строятся одна за другой, и чтобы построить di+1 достаточно показать, что fi применимо в di. Возьмем d0 = g0.
Предположим, что для всех j < i, fj применимо в конфигурации dj и dj+1 = fj (dj ). Пусть di = (cp1 , ..., cpN , M) и пусть fi =(c, x, y, d) будет событие в процессе р, тогда событие fi применимо в di, если сp = c и х Í М.
Чтобы показать, что сp = c нужно различать два случая. В обоих случаях мы должны помнить, что каузальный порядок исполнения Е абсолютно упорядочивает события в процессе р. Это подразумевает, что события в процессе р появляются в точно таком же порядке и в f и в Е’.
Случай 1: fi - первое событие в р из f, тогда ср – это начальное состояние р. Но тогда fi – также первое событие в р из Е’, что подразумевает, что с – это начальное состояние р. Следовательно, с = ср.
Случай 2: fi – не первое событие в р из f. Пусть последнее событие в р из f перед fi будет fi' = (c’, x’, y’, d’), тогда ср = d’. Но тогда fi' также последнее событие в р перед fi из Е’, что подразумевает, что с = d’. Следовательно, с = ср.
Чтобы показать, что х Í М мы должны помнить, что соответствующие события приема и посылки встречаются в одном порядке и в f и в Е’. Если fi не событие посылки, то х = Æ и х Í М выполняется тривиально. Если fi – это событие посылки, пусть fi будет соответствующим событием посылки. Так как fj í fi , j < i выполняется, т.е., событие посылки предваряет fi в f, следовательно, х Í М.
Мы сейчас показали, что для каждого i, fi применимо в di, и di+1 может быть взято как fi(di). Мы должны, наконец, показать, что последние конфигурации из F и Е совпадают, если Е конечно. Пусть gk будет последней конфигурацией из Е. Если Е’ не содержит события в р, то состояние р в gk равно его начальному состоянию. Так как f также не содержит события в р, то состояние р в dk также равно начальному состоянию, отсюда состояние р в dk равняется его состоянию в gk. Иначе, состояние р в gk есть состояние после последнего события в р из Е’. Это также последнее событие в р из f, так что это также состояние р в dk.
Сообщения в процессе передачи в gk есть такие сообщения, для которых событию посылки нет соответствующего события получения в Е’. Но так как Е’ и f содержат один и тот же набор событий, те же сообщения в процессе передачи в последней конфигурации из F.

Рис. 2.2 Пространственно-временная диаграмма эквивалентная рис. 2.1
Исполнения F и Е имеют один набор событий, и каузальный порядок этих событий – один и тот же для Е и F. Поэтому, также, в этом случае Е – это перестановка событий из F, которая согласуется с каузальным порядком исполнения F. Если применить условие теоремы 2.21, мы можем сказать, что Е и F – эквивалентные исполнения, что обозначается как E ~ F.
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62


