 Реферат: Распределенные алгоритмы
Реферат: Распределенные алгоритмы
В Таблице 6.19 дан список волновых алгоритмов, рассмотренных в этой главе. В столбце «Номер» дана нумерация алгоритмов в главе; в столбце «C/D» отмечено, является ли алгоритм централизованным (C) или децентрализованным (D); столбец «T» определяет, является ли алгоритм алгоритмом обхода; в столбце «Сообщения» дана сложность сообщений; в столбце «Время» дана временная сложность. В этих столбцах N - количество процессов, |E| - количество каналов, D - диаметр сети (в переходах).
| Алгоритм | Номер | Топология | C/D | T | Сообщения | Время |
| Раздел 6.2: Общие алгоритмы | ||||||
| Кольцевой | 6.2 | кольцо | C | да | N | N |
| Древовидный | 6.3 | дерево | D | нет | N | O(D) |
| Эхо-алгоритм | 6.5 | произвольная | C | нет | 2|E| | O(N) |
| Алгоритм опроса | 6.6 | клика | C | нет | 2N-2 | 2 |
| Фазовый | 6.7 | произвольная | D | нет | 2D|E| | 2D |
| Фазовый на кликах | 6.8 | клика | D | нет | N(N-1) | 2 |
| Финна | 6.9 | произвольная | D | нет | £4N|E| | O(D) |
| Раздел 6.3: Алгоритмы обхода | ||||||
| Последовательный опрос | 6.10 | клика | C | да | 2N-2 | 2N-2 |
| Для торов | 6.11 | тор | C | да | N | N |
| Для гиперкубов | 6.12 | гиперкуб | C | да | N | N |
| Тарри | 6.13 | произвольная | C | да | 2|E| | 2|E| |
| Раздел 6.4: Алгоритмы поиска в глубину | ||||||
| Классический | 6.14 | произвольная | C | да | 2|E| | 2|E| |
| Авербаха | 6.15 | произвольная | C | нет | 4|E| | 4N-2 |
| Сайдона | 6.16/6.17 | произвольная | C | нет | 4|E| | 2N-2 |
| Со знанием соседей | 6.18 | произвольная | C | да | 2N-2 | 2N-2 |
Замечание: фазовый алгоритм (6.7) и алгоритм Финна (6.9) подходят для ориентированных сетей.
Таблица 6.19 Волновые алгоритмы этой главы.
Сложность распространения волн в сетях большинства топологий значительно зависит от того, централизованный алгоритм или нет. В Таблице 6.20 приведена сложность сообщений централизованных и децентрализованных волновых алгоритмов для колец, произвольных сетей и деревьев. Таким же образом можно проанализировать зависимость сложности от других параметров, таких как знание соседей или чувство направления (Раздел B.3).
| Топология | C/D | Сложность | Ссылка |
| Кольцо | C | N | Алгоритм 6.2 |
| D | O(N logN) | Алгоритм 7.7 | |
| Произвольная | C | 2|E| | Алгоритм 6.5 |
| D | O(N logN + |E|) | Раздел 7.3 | |
| Дерево | C | 2(N-1) | Алгоритм 6.5 |
| D | O(N) | Алгоритм 6.3 |
Таблица 6.20 Влияние централизации на сложность сообщений.
В Подразделе 6.1.5 было показано, что за одну волну можно вычислить инфимум по входам всех процессов. Вычисление инфимума может быть использовано для вычисления коммутативного, ассоциативного и идемпотентного оператора, обобщенного на входы, такого как минимум, максимум, и др. (см. Заключение 6.14). Большое количество функций не вычислимо таким образом, среди них - сумма по всем входам, т.к. оператор суммирования не идемпотентен. Суммирование входов может быть использовано для подсчета процессов с определенным свойством (путем присваивания входу 1, если процесс обладает свойством, и 0 в противном случае), и результаты этого подраздела могут быть распространены на другие операторы, являющиеся коммутативными и ассоциативными, такие как произведение целых чисел или объединение мультимножеств.
Оказывается, не существует общего метода вычисления сумм с использованием волнового алгоритма, но в некоторых случаях вычисление суммы возможно. Например, в случае алгоритма обхода, или когда процессы имеют идентификаторы, или когда алгоритм порождает остовное дерево, которое может быть использовано для вычисления.
Невозможность существования общего метода. Невозможно дать общий метод вычисления сумм с использованием произвольного волнового алгоритма, подобного методу, использованному в Теореме 6.12 для вычисления инфимумов. Это может быть показано следующим образом. Существует волновой алгоритм для класса сетей, включающего все неориентированные анонимные (anonymous) сети диаметра два, а именно, фазовый алгоритм (с параметром D=2). Не существует алгоритма, который может вычислить сумму по всем входам, и который является правильным для всех неориентированных анонимных (anonymous) сетей диаметра два. Этот класс сетей включает две сети, изображенные на Рис.6.21. Если предположить, что каждый процесс имеет вход 1, ответ будет 6 для левой сети и 8 - для правой. Воспользовавшись технологией, представленной в Главе 9, можно показать, что любой алгоритм даст для обеих сетей один и тот же результат, следовательно, будет работать неправильно. Детальное доказательство оставлено читателю в Упражнении 9.7.
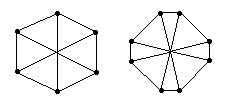
Рис.6.21 Две сети диаметра два и степени три.
Вычисление сумм с помощью алгоритма обхода. Если A - алгоритм обхода, сумма по всем входам может быть вычислена следующим образом. Процесс p содержит переменную jp, инициализированную значением входа p. Маркер содержит дополнительное поле s. Всякий раз, когда p передает маркер, p выполняет следующее:
s := s + jp ; jp := 0
и затем можно показать, что в любое время для каждого ранее пройденного процесса p jp = 0 и s равно сумме входов всех пройденных процессов. Следовательно, когда алгоритм завершается, s равно сумме по всем входам.
Вычисление суммы с использованием остовного дерева. Некоторые волновые алгоритмы предоставляют для каждого события принятия решения dp в процессе p остовное дерево с корнем в p, по которому сообщения передаются по направлению к p. Фактически, каждое вычисление любого волнового алгоритма содержит такие остовные деревья. Однако, может возникнуть ситуация, когда процесс q посылает несколько сообщений и не знает, какие из его исходящих ребер принадлежат к такому дереву. Если процессы знают, какое исходящее ребро является их родителем в таком дереве, дерево можно использовать для вычисления сумм. Каждый процесс посылает своему родителю в дереве сумму всех входов его поддерева.
Этот принцип может быть применен для древовидного алгоритма, эхо-алгоритма и фазового алгоритма для клик. Древовидный алгоритм легко может быть изменен так, чтобы включать сумму входов Tpq в сообщение, посылаемое от p к q. Процесс, который принимает решение, вычисляет окончательный результат, складывая величины из двух сообщений, которые встречаются на одном ребре. Фазовый алгоритм изменяется так, чтобы в каждом сообщении от q к p пересылался вход q. Процесс p складывает все полученные величины и свой собственный вход, и результат является правильным ответом, когда p принимает решение. В эхо-алгоритме входы могут суммироваться с использованием остовного дерева T, построенного явным образом во время вычисления; см. Упражнение 6.15.
Вычисление суммы с использованием идентификации. Предположим, что каждый процесс имеет уникальный идентификатор. Сумма по всем входам может быть вычислена следующим образом. Каждый процесс помечает свой вход идентификатором, формируя пару (p, jp); заметим, что никакие два процесса не формируют одинаковые пары. Алгоритм гарантирует, что, когда процесс принимает решение, он знает каждый отдельный вход; S = {(p, jp): p Î P} - объединение по всем p множеств Sp = {(p, jp)}, которое может быть вычислено за одну волну. Требуемый результат вычисляется с помощью локальных операций на этом множестве.
Это решение требует доступности уникальных идентификаторов для каждого процесса, что значительно увеличивает битовую сложность. Каждое сообщение волнового алгоритма включает в себя подмножество S, которое занимает N*w бит, если для представления идентификатора и входа требуется w бит; см. Упражнение 6.16.
6.5.3 Альтернативные определения временной сложности
Временную сложность распределенного алгоритма можно определить несколькими способами. В этой книге при рассмотрении временной сложности всегда имеется в виду Определение 6.31, но здесь обсуждаются другие возможные определения.
Определение, основанное на более строгих временных предположениях. Время, потребляемое распределенными вычислениями, можно оценить, используя более строгие временные предположения в системе.
Определение 6.37 Единичная сложность алгоритма (one-time complexity) - это максимальное время вычисления алгоритма при следующих предположениях.
O1. Процесс может выполнить любое конечное количество событий за нулевое время.
O2. Промежуток времени между отправлением и получением сообщения - ровно одна единица времени.
Сравним это определение с Определением 6.31 и заметим, что предположение O1 совпадает с T1. Т.к. время передачи сообщения, принятое в T2, меньше или равно времени, принятому в O2, можно подумать, что единичная сложность всегда больше или равна временной сложности. Далее можно подумать, что каждое вычисление при предположении T2 выполняется не дольше, чем при O2, и, следовательно, вычисление с максимальным временем также займет при T2 не больше времени, чем при O2. Упущение этого аргумента в том, что отклонения во времени передачи сообщения, допустимые при T2, порождают большой класс возможных вычислений, включая вычисления с плохим временем. Это иллюстрируется ниже для эхо-алгоритма.
Фактически, верно обратное: временная сложность алгоритма больше или равна единичной сложности этого алгоритма. Любое вычисление, допустимое при предположениях O1 и O2, также допустимо при T1 и T2 и занимает при этом такое же количество времени. Следовательно, наихудшее поведение алгоритма при O1 и O2 включено в Определение 6.31 и является нижней границей временной сложности.
Теорема 6.38 Единичная сложность эхо-алгоритма равна O(D). Временная сложность эхо-алгоритма равна Q(N), даже в сетях с диаметром 1.
Доказательство. Для анализа единичной сложности сделаем предположения O1 и O2. Процесс на расстоянии d переходов от инициатора получает первое сообщение <tok> ровно через d единиц времени после начала вычисления и имеет глубину d в возникающем в результате дереве T. (Это можно доказать индукцией по d.) Пусть DT - глубина T; тогда DT £ D и процесс глубины d в T посылает сообщение <tok> своему родителю не позднее (2DT + 1) - d единиц времени после начала вычисления. (Это можно показать обратной индукцией по d.) Отсюда следует, что инициатор принимает решение не позднее 2DT + 1 единиц времени после начала вычисления.
Для анализа временной сложности сделаем предположения T1 и T2. Процесс на расстоянии d переходов от инициатора получает первое сообщение <tok> не позднее d единиц времени после начала вычисления. (Это можно доказать индукцией по d.) Предположим, что остовное дерево построено через F единиц времени после начала вычисления, тогда F £ D. В этом случае глубина остовного дерева DT необязательно ограничена диаметром (как будет показано в вычислении ниже), но т.к. всего N процессов, глубина ограничена N-1. Процесс глубины d в T посылает сообщение <tok> своему родителю не позднее (F+1)+(DT-d) единиц времени после начала вычисления. (Это можно показать обратной индукцией по d.) Отсюда следует, что инициатор принимает решение не позднее (F+1)+DT единиц времени после начала вычисления, т.е. O(N).
Чтобы показать, что W(N) - нижняя граница временной сложности, построим на клике из N процессов вычисление, которое затрачивает время N. Зафиксируем в клике остовное дерево глубины N-1 (на самом деле, линейную цепочку вершин). Предположим, что все сообщения <tok>, посланные вниз по ребрам дерева, будут получены спустя 1/N единиц времени после их отправления, а сообщения <tok> через листовые ребра будут получены спустя одну единицу времени. Эти задержки допустимы, согласно предположению T2, и в этом вычислении дерево полностью формируется в течение одной единицы времени, но имеет глубину N-1. Допустим теперь, что все сообщения, посылаемые вверх по ребрам дерева также испытывают задержку в одну единицу времени; в этом случае решение принимается ровно через N единиц времени с начала вычисления.
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62


