Реферат: Распределенные алгоритмы

                           Vi = Vi È{ uj: j <l}  и  Ei+1 = Ei È {( uj, uj+1) : j < 1}.

(Построение иллюстративно представлено на Рисунке 4.1.) Нетрудно видеть что Ti поддерево Ti+1 и что vi+1 Î Vi+1. Чтобы увидеть что Ti+1  дерево, заметим что по построению Ti+1 связный, и число вершин превосходит число ребер на одно. (To имеет последнее свойство, на каждом шаге  много вершин и ребер добавлено)

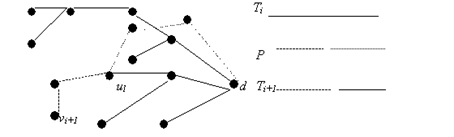
Рисунок 4.1 Построение Ti+1.

Осталось показать, что для всех w Î Vi+1 , (уникальный) путь от w к d в Ti+1 - оптимальный путь от  w к d в G. Для вершин  w Î Vi Ì Vi+1  это следует, потому что Ti  поддерево Ti+1 ;  путь от w к d в Ti+1   точно такой же, как путь в Ti, который оптимален. Теперь пусть w = uj, j < l  будет вершиной в Vi+1 \V,.  Запишем Q для пути от ui к  d в Ti, тогда в Ti+1  uj соединена с  d через путь <uj, . . . , ul> соединенный с Q, и осталось показать, что этот путь оптимальный в G. Во-первых, суффикс P' = <ul, . . . , uk>  в P  оптимальный путь от ul  до d, т.е., C(P') = C(Q): оптимальность Q подразумевает что C(P') ³C(Q), и C(Q)< C(P') подразумевает (добавлением стоимости пути) что путь <uo, . . . , ul> соединен с Q имеющий меньший путь, чем P, противоречащий оптимальности  P. Теперь положим, что R из uj к d имеет меньшую стоимость, чем путь <uj, . . . , ul> соединенный с Q. Тогда, по предыдущим наблюдениям, R имеет меньшую стоимость, чем суффикс <uj, . . . , uk>   P, и это предполагает что путь <uo, . . . , uj> соединенный с  R имеет меньшую стоимость,  чем P, противоречащий оптимальности  P.                                                    Ž

Дерево охвата, приложенное к d , называется деревом стока для d, и дерево со свойством, данным в Теореме 4.2 , называется оптимальным деревом стока. Существование оптимальных деревьев стока  не является компромиссом оптимальности, если только алгоритмы маршрутизации  рассматриваются, для которого механизм пересылки, как в Алгоритме 4.2. В этом алгоритме, table_lookupu локальная процедура с одним параметром, возвращая соседа u (после консультации с таблицами маршрутизации). Действительно, поскольку все пакеты для адресата d могут быть направлены оптимально используя дерево обхвата, приложенное к d, пересылка оптимальна, если, для всего u¹d, table_lookupu(d)  возвращает отца u в  дереве охвата Td.

Когда механизм пересылки имеет эту форму, и никакие (дальнейшие) изменения топологии не происходят, корректность таблиц маршрутизации может быть удостоверена, используя следующий результат. Таблицы маршрутизации, как говорят,  содержат цикл (для адресата d), если существуют узлы u1, . . . , uk такие, что для всех i , ui ¹d, для всех i < k, table_lookupu(d) = ui+1, и table_lookupu(d) = uj+1.. Таблицы, как говорят,  являются свободным от циклов, если они не содержат циклов для любого d.

(* Пакет с адресатом d был получен или сгенерирован в узле u *)

if d=u

          then доставить «местный» пакет

          else послать пакет к table_lookupu (d)

Алгоритм 4.2 Адресат-основанная пересылка (для узла u).

Лемма 4.3 Механизм пересылки доставляет каждый пакет  адресату, тогда и только тогда когда  таблицы маршрутизации цикл-свободны.

Доказательство. Если таблицы содержат цикл для некоторого адресата d,  пакет для d никогда не будет доставлен, если источник - узел в цикле.

Примем, что  таблицы цикл-свободны и позволяют пакету с адресатом d (и источник uo) быть посланным через uo, u1, u2, . .. если один встречается дважды в этой последовательности, скажем ui = uj, тогда таблицы содержат цикл, а именно < ui  ..., uj> противореча предположению, что таблицы являются цикл-свободными. Таким образом, каждый узел входит единожды, что подразумевает, что эта последовательность конечна, заканчивающаяся, скажем, в узле Великобританию uk (k < N). Согласно процедуре пересылки последовательность может  заканчиваться только в d , то есть, uk = d, и пакет достиг адресата за не больше чем N — 1 шагов 

В некоторых алгоритмах маршрутизации  случается, что таблицы не цикл-свободны в течение их вычисления. Когда такой алгоритм используется, пакет может пересекать цикл в течение вычисления таблиц, но достигает адресата не больше чем N — 1 шагов после завершения вычисления таблицы, если изменения топологии прекращаются. Если изменения топологии не прекращаются, то есть, сеть подчинена бесконечной последовательности изменений топологии, пакеты не обязательно достигают своего адресата, даже если таблицы цикл-свободны во время модификаций;

Ветвящаяся маршрутизация с минимальной задержкой. При маршрутизации через пути с минимальной задержкой требуется, и задержка канала зависит от использования (таким образом, предположение (1) в начале этого раздела не имеет силу), стоимость использования пути не может просто быть оценена как функция этого единственного пути. Кроме того, трафик на канал должен быть принят во внимание. Избегать скопления пакетов (и возникающую в результате этого задержку) на пути, обычно необходимо посылать пакеты, имеющие ту же самую пару исходный-адресат через различные пути; трафик для этой пары "распределяется" в один или большее количество узлов промежуточного звена как изображено в Рисунке 4.3. Методы маршрутизации, которые используют различные пути к одному адресату,  называются много-путевыми или ветвящимися методами маршрутизации. Потому что ветвящиеся методы маршрутизация  являются, обычно, очень запутанными, они не будет рассматриваться в этой главе

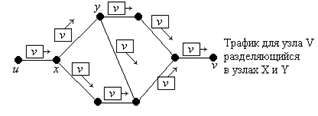
Рисунок 4.3 Пример буферизованной маршрутизации.

4.2 Проблема кротчайших путей всех пар

Этот раздел обсуждает алгоритм Toueg [Tou80a] одновременного вычисления  таблицы маршрутизации для всех узлов в сети. Алгоритм вычисляет для каждой пары (u, v) узлов длину самый короткий пути от u до v и сохраняет первый канал такого пути в u. Проблема вычисления самого короткого пути между любыми двумя узлами графа известна как  проблема кротчайшего пути всех пар. Распределенный алгоритм Toueg для этой проблемы основан на централизованном  алгоритме Флойда-Уошалла [CLR90, Раздел 26.4]. Мы обсудим алгоритм Флойда-Уошалла в Подразделе 4.2.1, и впоследствии алгоритм Toueg в Подразделе 4.2.2. Краткое обсуждение некоторых других алгоритмов для проблемы кротчайших путей всех пар следует в Подразделе 4.2.3 ..                                

4.2.1 Алгоритм Флойда-Уошала

Пусть дан взвешенный граф G = (V, E) , где вес ребра uv дан wuv . Не обязательно допускать что wuv= wvu , но допустим, что граф не содержит циклов с общим отрицательным весом. Вес пути  < uo, ..., uk> определяется как  . Дистанция от u до v, обозначенная d(u, v), наименьший вес любого пути от u к v (¥  если нет такого пути). Проблема кротчайших путей всех пар - вычисление d(u, v) для каждых u и v.

Для вычисления всех расстояний, алгоритм  Флойда-Уошала использует понятие  S-путей; это пути, в которых все промежуточные вершины принадлежат к подмножеству S из V.

Определение 4.4.  Пусть S - подмножество V. Путь < uo  ..., uk> -S-путь если для любого i, 0 <i < k,  uj Î S.  S-расстояние от u до v, обозначенное dS(u. v), наименьший вес любого S-пути от u до v (¥  если такого пути нет).

Алгоритм стартует рассмотрением всех Æ-путей, и увеличивая вычисления S-путей для больших подмножеств S, до тех пор пока V-пути будут рассмотрены. Могут быть сделаны следующие наблюдения.

Утверждение 4.5 Для всех u и S, dS(u, u) = 0. Более того, S-пути удовлетворяют следующим правилам для u¹ v.

(1) Существует Æ -путь от u к v тогда и только тогда когда uv ÎE.

(2) Если uv Î E тогда dS(u, v) = wuv  иначе dS(u, v) =¥ .

(3) Если  S'=S È{w} тогда простой S'-путь от и к v - S-путь от u к v или S-путь от u к w соединенные  S-путем от w к v.

(4) Если S' = S È{w} тогда dS’ (u, v)=min(dS (u, v), dS (u, w)+ dS (w, v)).

(5) Путь от u до v существует тогда и только тогда когда V-путь от u к v существует

(6) d(u, v)= dV (u, v),

Доказательство. Для всех u и S  dS (u, u) £.0 по причине того, что пустой путь (состоящий из 0 ребер) это  S-путь от u к u с весом 0. Нет путей, имеющих меньший вес, потому что G не содержит циклов отрицательного веса, таким образом, dS (u, u) = 0.

Для (1):  Æ -путь не содержит промежуточных узлов,  так  Æ - путь от u к v

состоит только из канала  uv.

Для (2): следует непосредственно из (1).

Для (3): простой S’-путь от u к v содержит узел w единожды, или 0 раз как промежуточный. Если он не содержит w как промежуточную вершину он  S-путь, иначе он - конкатенация двух S-путей, один к  w и один из w.

Для(4): Это можно доказать применив  Лемму 4.1 . Получим что  (если S’-путь от u в v существует) это  простой S' -путь длиной dS’(u, v) от u к v, такой, что  dS’(u, v) = min(dS (u, v), dS (u, w) + dS (w, v) ) по (3).

Для (5): каждый  S-путь - путь, и обратно.

Для (6): каждый  S-путь - путь, и обратно, следовательно, оптимальный V-путь  также оптимальный путь.

_____________________________________________________________________

begin (* Инициализация S = Æ  и D = Æ-дистанция *)

       S:=0;

forall u,v do

if u = v then  D[u, v] := 0

                           else

if uv Î E then D[u, v] := wuv

                                                              else D[u. v] := ¥  ;

      (* Расширим S  «центральными точками» *)

      while S ¹ V do

                (* Цикл инвариантен: "u, v : D[u, v] = dS (u, v) *)

                begin выбрать  w из V \ S ;

                          (* Выполнить глобальную w-центровку *)

forall u Î V do

                                 (* Выполнить локальную w-центровку u *)

forall  v ÎV do

                                          D[u. v] := min ( D[u, v], D[u, w] + D[w, v] ) ;

                                         S:=S È{w}

                end   (*"u, v : D[u, v] = dS (u, v)*)

 end

Алгоритм4.4 Алгоритм Флойда-Уошалла.

Используя Утверждение 4.5 не сложно разработать алгоритм  "динамического программирования" для  решения проблемы кротчайших путей всех пар; смотри см. Алгоритм 4.4. Алгоритм вначале считает 0-пути, и, увеличивая, вычисляет  S-пути для больших множеств S (увеличивая  S   "центральными" кругами), до тех пор, пока  все пути не будут обсуждены.

Теорема 4.6 Алгоритм 4.4 вычисляет расстояние между всеми парами узлов за Q(N3) шагов.

Доказательство. Алгоритм начинает с D[u, v] = 0,   если u = v, D[u, v] = wuv , если uv Î E и D[u, v] = ¥  в другом случае, и S = 0. Следуя из Утверждения 4.5, частей (1) и (2), "u, v имеет силу  D[u, v] = dS (u, v) . В центральной окружности с центральной вершиной w  множество S расширено узлом w, и означивание  D[u, v] гарантирует (по частям (3) и (4) утверждения) что утверждение "u, v : D[u, v] = dS(u, v)  сохранено как инвариант цикла. Программа заканчивает работу, когда S = V, т.е., (по частям (5) и (6) утверждения и инварианту цикла)  S-расстояние эквивалентно расстоянию.

Главный цикл  выполняется N  раз, и содержит N2 операций (которые могут быть выполнены параллельно или последовательно), откуда и следует временная граница  данная теоремой.ˆ

_____________________________________________________________________                                                   

var Su    : множество вершин;

       Du   : массив весов;

       Nbu : массив вершин;

begin Su :=Æ  ;

      forall v Î V do

            if v = u

                  then begin Du [v] :=0 ; Nbu[v] := udef  end

            else if v Π Neighu

                  then begin Du[v] := wuv ; Nbu[v] := v end

            else begin Du[v] := ¥ ; Nbu[v] := udef end ;

      while Su¹ V do

           begin выбрать w из V \ Su ;

                     (* Все вершины должны побывать вершиной w *)

                      if u == w

                             then "распространить таблицу Dw"

                             else   "принять таблицу Dw"

                       forall v Î V do

                             if Du[w] + Dw[v] < Du[v] then

                                  begin Du[v]:= Du[w] + Dw[v] ;

                                             Nbu[v] := Nb[w]

                                  end;

                                  Su := Su U {w}

                       end

          end;

Алгоритм 4.5 Простой алгоритм (Для узла u).

4.2.2 Алгоритм кротчайшего пути.(Toueg)

Распределенный алгоритм вычисления  таблиц маршрутизации бал дан Toueg [TouSOa], основанный на алгоритме Флойда-Уошалла описанном в предыдущей части. Можно проверить что алгоритм Флойда-Уошалла подходит для этих целей, т.е., что  его ограничения реалистичны для распределенных систем. Наиболее важное ограничение алгоритма что граф не содержит циклов отрицательного веса. Это ограничение действительно реально для распределенных систем,  где обычно каждый отдельный канал означен положительной оценкой. Даже можно дать более строгое ограничение; смотри A1 ниже. В этой части даны следующие ограничения.

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62