Реферат: Шпоры по математическому анализу

Докаательство: Оно может быть сведено к применению известной теоремы для функции одной переменной. В наших условиях функция f(x,y0) имеет экстремум в точке  x0, т.к. неравенство f(х0+∆х, y0+∆у)≤f(х0, y0), иначе ∆f≤0

Или ∆f≥0 должно, в частности, выполнятся и при ∆у=0. Поэтому, d/dx∙f(x,y0)=0 при х=х0, а это то же самое, что f'x(х0, y0)=0. Аналогично устанавливается, что f'у(х0, y0)=0. Экстремум возможен и тогда, когда одна или обе частные производные не существуют, что тоже является необходимым условием экстремума. Т.о., необходимые условия экстремума формулируются так: для каждой из частных производных выполняется одно из двух - лиюл она существует и равна нулю, либо она не существует.

31. Предел и непрерывность функции двух переменных.

Определение: Число А называется пределом по совакупности переменных функции f(x,y) при стремлении х к х0 и у к у0, если для любого ε>0 существует такое δ>0, что для всех точек (x,y), координаты которых удовлетворяют неравенствам │ х - х0 │< δ, │ y - y0 │< δ ( за исключением, быть может, точки (х0, y0)), выполняется неравенство │f(x,y)-A│ < ε. Применяется обозначение

Заметим, что точка (х0, y0) может не принадлежать ООФ f(x,y).

Пусть функция f(x,y) определена в области D.

Определение. Если выполняются три условия:

1.     (х0, y0)Î D;

2.     существует

3.

то функция называется непрерывной в точке (х0, y0).

Определение: Если не выполняется хотя бы одно из этих условий, то функцию называют разрывной в точке (х0, y0), а саму точку называют точкой разрыва.

Определение: Функция называется непрерывной в области, если она непрерывна в каждой точке этой плоскости.

Определение: Функция z = f(x,y) называется непрерывной в точке (х0, y0), если при стремлении к нулю приращений ∆х, ∆у, независимых переменных стремится к нулю полное приращение ∆z функции f(x,y) (здесь  предполагается выполнение условий 1 и 2.) (∆z - полное приращение).

42. Условный экстремум, метод множителей Лагранжа для функции двух переменных.

В этом методе не требуется выражать явно y через х , однако используется то обстоятельство, что в случае предполагаемой замены y на g(x) дело сводится к безусловному экстремуму функции одной переменной.

Итак, находим полную прозводную от z по х, считая y функцией х:

В точках экстремума dz: dx=0, следовательно (1),

Применим снова правило дифференцирования сложной функции к уравнению φ(x,y)=0. Будем предполагать при этом, что у заменен той самой функцией х, которая неявно задается уравнением. Такая замена превращает уравнение φ(x,y)=0 в тождество. Получим (2):

Умножим (2) на неопределенный множитель λ и сложим с (1):

Мы будем предполагать, что в точке экстремума ¶j¸¶у¹0. Тогда существует число l, при котором ¶f¸¶y + l(¶j¸¶у) = 0 в этой точке. Из равенства (3) следует, что в этой точке ¶f¸¶х + l(¶j¸¶х) = 0

Мы приходим к необходимым условиям экстремума (4):

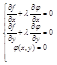
В этой системе из трех уранений три неизвестные величины x, y и l. Из системы находятся одна или несколько точек (х,у). Что касается l, то этот множитель играет вспомогательную роль и дальше не требуется. Найденные точки (х,у) проверяют на наличие в них экстремума и его вид (максимум или минимум). В  случае необходимости вычисляются значения f(x,y) на концах промежутка, ограничивающего изменение х при описании кривой АВ. Часто из существа задачи легко решается вопрос, с каким из значений - наибольшим или наименьшим - мы имеем дело. Проведенные рассуждения обосновывают метод Лагранжа, который состоит в следующем.

Составляется вспомогательная функция

F (x,y,l) = f(x,y) + lj(x,y) (5), называемая функцией Лагранжа. Для нее выписываются как для  функции трех переменных необходимые условия абсолютного экстремума:

При этом получается в точности система (4).

Коэффициент l называют множителем Лагранжа.

Метод Лагранжа допускает обобщение на функции большего числа переменных. Так, в задаче на условный экстремум функции u=f(x,y,z) с ограничениями j1(x,y,z)=0 и j2(x,y,z)=0 функция Лагранжа имеет вид:

F(x,y,z, l1, l2) = f(x,y,z) + l1j1(x,y,z)+ l2j2(x,y,z).

Нулю приравниваются все произвоные по x,y,z, l1, l2.

41. Достаточные условия  абсолютного экстермума функции двух переменных.

Обратимся к формуле Тейлора (вопр. 11). Нас интересует случай, когда необходимые условия экстремума выполняются, т.к. в противном случае вопрос решается однозначно - экстремума нет. Поэтому будем считать:

И, перенеся  f(х0,y0) в левую часть, получим слева

Кроме того, обозначим

Приводим к формуле:

Положим u = AΔx2 + 2B∆xΔy +CΔy2   При ρ→0 квадратичная форма u убывает со скоростью р2, т.е. быстрее. Поэтому в достаточно малой окрестности точки (х0,, y0) ,будет выполнятся неравенство 1/2│u│>│R│(если u не обратится в нуль). Это означает, что знак приращения совпадает со знаком u. Разумеется, в точках, где u=0, знаки ∆f и R совпадают. Имеются 3 возможности:

1.     Величина u сохраняет знак, обращаясь в нуль только при ∆x=∆y=0. Такая квадратичная форма называется знакоопределенной. В этом случае сохраняет знак и приращение ∆f . При ∆f≤0 в точке (х0,, y0)  имеется максимум, а при ∆f≥0 - минимум.

2.     В любой оокрестности точки (х0,, y0) величина u принимает как положительные, так и отрицательные значения. Такая квадратичная форма называется знакопеременной. В этом случае меняет знак и приращение ∆f . Экстремума нет.

3. Величина u сохраняет знак, но обращается в нуль не только в начале координат. Такая квадратичная форма называется знакопостоянной. В этом случае никакого вывода сделать нельзя без исследования остаточного члена. Если в точках названной прямой остаточный член меняет знак, то экстремума нет, если сохраняет тот же знак, что и величина u - экстремум есть, если сохраняет знак противоположный u - экстремума нет.

Дело свелось теперь к установлению условий, при которых квадратичная форма u является знакоопределенной, знакопеременной или знакопостоянной. Если А = С = 0, В ¹ 0, то u = В∆х∆у, и квадратичная форма является знакопеременной. При совпадении знаков ∆х и ∆у она имеет знак В, при несовпалении - знак противоположный знаку В. В этом случае экстремума нет. Если к тому же В = 0, вопрос об экстремуме решается путем исследования остаточного члена R в каждом конкретном случае.

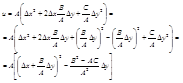
Пусть теперь хотя бы одна из величин А, С отлична от нуля. Положим для определенности, что А ≠ 0. Преобразуем форму u: вынесем за скобки А, прибавим и вычтем (В¸А ∆у)2. Первые три слагаемых представляют полный квадрат, два последних приводим к общему знаменателю:

1. Если В2 - АС <0, то форма знакоопределенная. Действительно,

Поэтому выражение в квадратных скобках неотрицательно и может обратится в нуль только тогда, когда оба слагаемых равны нулю. Второе обращается в 0 лишь при ∆у=0. В этом случае первое слагаемое будет равно 0 только при ∆х=0. Очевидно, что знак знакоопределенной формы u совпадает со знаком числа А.

2. Если В2 - АС >0, то форма знакопеременная. Действительно, выражение в квадратных скобках останется ∆x2 и если ∆х≠0., то ∆x2 > 0; при ∆у≠0 можно взять ∆х = -В/А∆у и выражение в квадратных скобках будет отрицательным.

3. Если В2 - АС = 0, то форма знакопостоянная. В скобках останется выражение (∆х+В/А∆у)2, которое неотрицательно. Но в нуль оно обращается не только при ∆х=∆у=0, а и тогда, когда ∆х = -В/А∆у, при любом ∆у.

33. Частные производные.

Наряду с полным приращением функции вводится понятие частных приращений по х ∆хz и по у ∆уz. Они определяются формулами, где приращение дается только одной из переменных.

Определение: Частной производной функции f(x,y) по х называется предел отношения частного приращения ∆хz к приращению ∆х, когда х→0 (если этот предел существует)(1)

Аналогично определяется частная производная функции z=f(x,y) по у. Для частной производной функции нескольких переменных, производную функции одной переменной называют переменной иногда обыкновенной.

Формуле (1) можно дать такое толкование: у функции f(x,y) фиксируется значение переменной у и получается, что f(x,y) становится функцией одной переменной х, а частная производная - обыкновенной производной этой функции. Так же истолковывается формула для f'y(x,y) с той разницей, что f(x,y) рассматривается как функция одной переменной у. Мы приходим к следующему правилу.

Для вычисления частной производной по х следует переменную у (или другие переменные, если их несколько) считать постоянной и вычислять производную по х как обыкновенную.

Аналогично формулируется правило вычисления частной производной по у.

32. Свойства непрерывных функций двух переменных.

1. Функция, непрерывная в замкнутой ограниченной области D а) ограничена в области

б) достигает в этой области наибольшего М и наименьшего m значений.

2. Сумма, произведение и частное непрерывных функций есть снова непрерывная функция, если в последнем случае делитель не принимает нулевого значения.

19. Определенный интеграл. Определение. Геометрический смысл.

Определение: Пусть дана функция y=f(x), ограниченная на отрезке [a,b] (a<b). Сделаем разбиение R этого отрезка точками хi: а<х0< x1< x2<…< xn,=b. Обозначим

На каждом промежутке [xi, xi+1] выберем произвольную точку ξi. Величину

Называют интегральной суммой.

Если существует предел интегральной суммы sR при  λR →0. Независящий от выбора разбиений R и выбора точек ξi, то он называется определенным интегралом от функции f(x) на отрезке [a,b] и обозначается (1)

Добавление к определению:

1. При a>b полагают

2. принимают

В интеграле (1) числа a и b называются соответственно нижними и верхними пределами интегрирования. Если функция f(x) ≥0 на отрезке [a,b], то геометрический смысл определенного интеграла - это площадь криволинейной трапеции. Пусть на промежутке [a,b] задана ограниченная функция y=f(x), будем считать ее положительной.(рис 1)

Фигура aABb, ограниченная графиком функции y=f(x), отрезком [a,b] оси х и перпендикулярами аА и bB к оси х, называется криволинейной трапецией. Измерить ее площадь  непосредственно путем установления того, сколько раз в этой фигуре укладывается единица измерения площади (квадрат со стороной, равной единице), и доли этой единицы невозможно из-за криволинейной верхней границы.

Разобьем  отрезок [a,b] на части (не обязательно равные) точками хi (i = 0,n): а=х0< x1< x2<…< xn=b. Это разбиение назовем R. Длину наибольшего отрезка назовем

На каждом из частичных отрезков [xi, xi+1] выберем произвольную точку

И построим прямоугольник с высотой f(ξi). В результате получится ступенчатая фигура, ограниченная сверху ломаной линией L. Ее площадь назовем sR. Если теперь увеличивать число делений разбиения R так, что бы λR →0, то ломаная L будет все теснее прижиматься к кривой АВ. Это дает возможность ввести следующее определние.

Определение: Площадью криволинейной трапеции aAАb называется предел, к которому стремится площадь sR ступенчатой фигуры когда число делений разбиения R не ограничено возрастает и λR →0 (Если этот предел существует и не зависит от способа получения разбиения R и выбора точек ξi).

28. Вычисление площади фигуры и длины дуги с помощью определенного интеграла.

f(x)≥0

Рассмотрим два случая.

1. площадь S заштрихованной фигуры на рис 1, а, где функция y=f(x) на отдельных промежутках принимает отрицательное значение, выражается формулой:

2. Площадь S фигуры ограничена графиками функции y=f(x) и y=g(x), а так же прямыми АВ и CD (рис 2) вычисляется по формуле:

Определение: Пусть дана дуга кривой АВ. Нанесем на нее произвольные точки Mi (i=0,n) и соединим их хордами (рис 3). Периметр полученной ломаной обозначим Pn. Будем увеличивать число точек Mi на дуге. Длиной дуги кривой АВ называется предел периметра Pn, когда длина наибольшей хорды стремится к нулю (если этот предел существует и не зависит от выбора вершин ломаной). Если дуга задана уравнением y=f(x) на промежутке [a,b] (ищем длину дуги l). Будем считать функцию f(x) непрерывно дифференцируемой. Положенеи произвольных точек Mi определим выбрав абциссы этих точек, т.е. сделав разбиение R отрезка [a,b] точками а=х0< x1< x2<…< xn=b. Длину хорды, соединяющей точки Mi и Mi+1 обозначим ∆li.Ее проекциями на оси координат будут ∆хi ∆уi. Очевидно,

Страницы: 1, 2, 3, 4, 5