Реферат: Прикладная математика

и минимизируют суммарные затраты за весь планируемый период

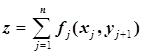                                                                                                     (3)

причем по смыслу задачи

                                    xj ³ 0, yj ³ 0,      j = 1,n                                                           (4)

Прежде чем приступить к решению поставленной задачи, заметим, что для любого месяца j величина yj+1 запаса к концу месяца должна удовлетворять ограничениям

0 £ yj+1 £ dj+1 + dj+2 + ... + dn                                                 (5)

т.е. объем производимой продукции xj на этапе j может быть настолько велик, что запас yj+1 удовлетворяет спрос на всех последующих этапах, но не

имеет смысла иметь yj+1 больше суммарного спроса на всех последующих этапах. Кроме того, из соотношений (2) и (4) непосредственно следует, что переменная xj должна удовлетворять ограничениям

0 £ xj £ dj + yj+1                                                          (6)

Следует также заметить, что переменные xj, yj могут принимать только целые неотрицательные значения, т.е. мы получили задачу целочисленного нелинейного программирования.

Будем решать задачу (1)-(6) методом динамического программирования.

Введем параметр состояния и составим функцию состояния.

25

За параметр состояния  x примем наличный запас в конце k -го месяца

                        x = yk+1                                                                                                (7)

а функцию состояния Fk(x) определим как минимальные затраты за первые k месяцев при выполнении условия (5)

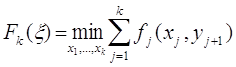                                                                           (8)

где минимум берется по неотрицательным целым значениям  x1,...,xk,  удовлетворяющим условиям

                                    xj + yj - dj = yj+1                              j = 1, k-1                                    (9)

                                    xk + yk - dk = x                                                                                      (10)

Учитывая, что

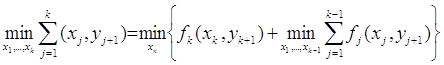           (11)

и величина запаса yk к концу (k-1) периода, как видно из уравнения (10), равна

                                    yk = x + dk - xk                                                                           (12)

приходим к рекуррентному соотношению

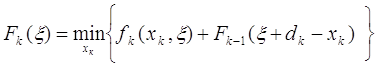                  (13)

где минимум берется по единственной переменной xk, которая, согласно (6) может изменяться в пределах

                        0 £ xk £ dk + x                                                             (14)

принимая целые значения, причем верхняя граница зависит от значений параметра состояния, изменяющегося в пределах

                                    0 £ x £ dk+1 + dk+2 + ... + dn                                                                     (15)

а индекс k может принимать значения

k = 2, 3, 4, ... , n                                                                      (16)

Если k=1, то

                                    F1(x = y2) = min f1(x1, x)                                                         (17)     

                                                              x1

где

 x1 = x + d1 - y1                                                                       (18)

                                    0£ x £ d2 + d3 + ... + dn                                                           (19)

26

т.е. на начальном этапе при фиксированном уровне y1 исходного запаса каждому значению параметра x отвечает только одно значение переменной x1, что несколько уменьшает объем вычислений.

Применив известную вычислительную процедуру динамического программирования, на последнем шаге (при k = n) находим значение последней компоненты xn* оптимального решения, а остальные компоненты определяем как

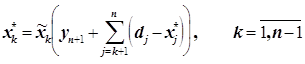                                (20)

Рассмотрим более подробно функции затрат fj(xj, yj+1) и рекуррентные соотношения. Пусть

jj(xj) = axj2 + bxj + c

jj (xj) - затраты на производство (закупку) xj единиц продукции на этапе j;

hj - затраты на хранение единицы запаса, переходящей из этапа j в этап j+1.

Тогда затраты на производство и хранение на этапе j равны

                        fj(xj, yj+1) = jj(xj) + hj yj+1 = axj2 + bxj + c + hj yj+1.                            (21)

Выведенные ранее рекуррентные соотношения динамического программирования для решения задачи управления производством и запасами в нашем случае принимают вид:

                      (22)

где

k = 2, 3, ... , n                                                                          (23)

0 £ yk+1 £ dk+1 + dk+1 + ... + dn                                                (24)

0 £ xk £ dk + yk+1                                                                     (25)

yk = yk+1 + dk - xk                                                                      (26)

(27)

Если же k=1, то

(30)

(29)

(28)

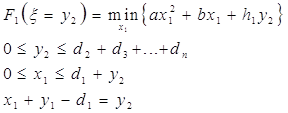
Остается заметить, что полезно обозначить выражение в фигурных скобках через

Wk(xk, yk+1) = axj2 + bxj + c + hkyk+1 + Fk-1(yk)                                    (31)

и записать рекуррентное соотношение (22) в виде

                        Fk(x=yk+1) = min Wk(xk, yk+1)                                                              (32)

                                                    xk

27

где минимум берется по целочисленной переменной xk, удовлетворяющей условию (25).

Пример. Рассмотрим трехэтапную систему управления запасами с дискретной продукцией и динамическим детерминированным спросом.

Пусть спрос (заявки) потребителей на нашу продукцию составляют: на первый этап d1=3 единицы, на второй –  d2=2, на третий -  d3=4 единицы. К началу первого этапа на складе имеется только 2 единицы продукции, т.е. начальный уровень запаса равен y1=2. Затраты на хранение единицы продукции на разных этапах различны  и составляют соответственно h1=1, h2=3, h3=2. Затраты на производство xj единиц продукции на j-м этапе определяются функцией

jj(xj) = xj2 + 5xj + 2                                                     (33)

т.е. а=1; b=5; с=2. Требуется указать, сколько единиц продукции на отдельных этапах следует производить, чтобы заявки потребителей были удовлетворены, а наши общие затраты на производство и хранение за все три этапа были наименьшими.

Исходные данные задачи можно кратко записать одной строкой:

d1      d2      d3      a      b      c       h1       h2        h3       y1

1        2       4       1      5      2       1        3         2        2

Воспользовавшись  рекуррентными  соотношениями,   последовательно   вычисляем

F1 (x = y2),  F2 (x = y3), ...,  Fk (x = yk+1), ...    и  соответственно  находим       1 (x= y2), 2 (x = y3 ), ..., `k (x = yk+1), ...

Положим k = 1. Согласно (27) имеем

                                                (34)

Учтем, что согласно (28) параметр состояния x = у2 может принимать целые значения на отрезке

0  у2  d2 + d3

                                                                  0  y2  2 + 4

т.е.

у2 = 0, 1, 2, 3, 4, 5, 6.

При этом, вообще говоря, каждому значению параметра состояния должна отвечать определенная область изменения переменной x1, характеризуемая условием (29)

0  х1  3 + у2

 

Однако, на первом этапе объем производства х1 не может быть меньше единицы, так как спрос d1 = 3, а исходный запас у1 = 2. Более того, из балансового уравнения

х1 + у1 - d1 = у2

непосредственно следует, что объем производства связан со значением параметра состояния  x= у2 соотношением

                        x1 =  y2 + d1 - y1 = y2 + 3 - 2 = y2 +1                                                  (35)

В этом и состоит особенность первого этапа. Если задан уровень запаса к  началу первого этапа, то каждому значению у2 отвечает единственное значение х1 и потому

                 F1(x = y2) = W1 (x1, y2)           

28

Придавая у2 различные целые значения от 0 до 6 и учитывая (35), находим

                 y2 = 0,  x1 = 0+1 = 1,   W1 (1;0) = 12 + 5×1 + 2 + 1×0 = 8

                 y2 = 1, x1 = 1+1 = 2,   W1 (2;1) = 22 + 5×2 + 2 + 1×1 = 17

и т.д. Значения функции состояния F1(x ) представлены в табл. 1

                                                                                                 Таблица 1

x = y2	0	1	2	3	4	5	6
F1 (x = y2)	8	17	28	41	56	73	92
x1(x=y2)	1	2	3	4	5	6	7

Переходим ко второму этапу. Полагаем k = 2 и табулируем функцию

F2(x = y3) с помощью соотношения (32)

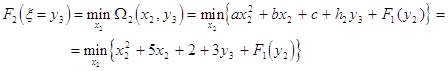        (37)

Здесь минимум берется по единственной переменной х2, которая может изменяться, согласно (25), в пределах

                        0 £ x2 £ d2 + y3    или    0 £ x2 £ 2 + y3                                              (38)

где верхняя граница зависит от параметра состояния x = у3, который, согласно (15), принимает значения на отрезке

0 £ y3 £ d3 ,    т.е.   0 £ y3 £ 4                                                             (39)

а аргумент у2 в последнем слагаемом справа в соотношении (37) связан с х2 и у3 балансовым уравнением

                                    x2 + y2 - d2 = y3

откуда следует

                                    y2 = y3 + d2 - x2 = y3 + 2 - x2                                                   (40)

Придавая параметру состояния различные значения от 0 до 4, будем последовательно вычислять  W2 (x2, x), а затем определять F2(x ) и 2(x ).             

Положим, например x = у3 = 2. Тогда, согласно (38),

0 £ x2 £ 4,

т.е. переменная х2 может принимать значения: 0, 1, 2, 3, 4, а каждому значению х2 отвечает определенное значение у2, вычисляемое по формуле (40):

у2 = 4 - х2

Последовательно находим:

если    x2 = 0,  то   y2 = 4-0 = 4,         W2 (0,2) = 02 + 5×0 + 2 + 3×2 + F1(4) = 8 + 56 = 64,

x2  = 1,        y2 = 4-1 = 3,          W2 (1,2) = 12 + 5×1 + 2 + 3×2 + F1(3) = 14 + 41 = 55,

x2 = 2,        y2 = 4-2 =2,           W2 (2,2) = 22 + 5×2 + 2 + 3×2 + F1(2) = 22 + 28 = 50,

x2  = 3,        y2 = 4-3 = 1,         W2 (3,2) = 32 + 5×3 + 2 + 3×2 + F1(1) = 32 + 17 = 49*,

x2 = 4,         y2 = 4-4 = 0,         W2 (3,2) = 42 + 5×4 + 2 + 3×2 + F1(0) = 44 + 8 = 52.

29

Наименьшее из полученных значений W2  есть F2 (2), т.е.

            F2 (x = y3 = 2) = min W2 (x2,2) = min (64, 55, 50, 49, 52) = 49,

                                                x2

причем минимум достигается при значении х2, равном

`2 (x = y3 = 2) = 3

Аналогично для значения параметра x = у3 = 3, проведя необходимые вычисления, найдем

F2 (x = y3 = 3) = 63;    `2 (x = y3 = 3) = 3.

Процесс табулирования функции F2 (x = y3) приведен в табл. 2, а результаты табулирования сведены в табл. 3.

Таблица 3

x= у3	0	1	2	3	4
F2 (x= y3)	24	36	49	63	78
(x= y3)	2	2	3	3	4

 Переходим к следующему этапу. Полагаем k=3 и табулируем функцию F3 (x = y4):

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10