Реферат: Программа государственного экзамена по математике для студентов математического факультета Московского городского педагогического университета

(в) правило умножения дробей: ;

(г), если ab ¹ 0;

в частности, справедливо известное правило деления дробей.

Доказательство. (а) Действительно, = (ac)×(bc)-1 = acc-1b = a×b-1 = .

(б) Имеем:  = (a + c)×b-1 = a×b-1 + c×b-1 = . И далее на основании уже доказанных свойств получаем .

Аналогично проверяются и два оставшихся пункта. ÿ

3. Арифметические функции: t(n), s(n), j(n).

10. Полная мультипликативность.

Определение. Числовой (арифметической) функцией называется функция, определенная на множестве Z+ целых положительных чисел и принимающая комплексные значения.

Числовая функция q называется вполне мультипликативной, если выполнены условия:

(1) ($x) q(x)¹0,

(2) для любых взаимно простых чисел x и y

q(xy)= q(x) q(y).

Заметим, что непосредственно из определения вытекает равенство

q(1)=1.

В самом деле, q(1)¹0, так как иначе данная функция q была бы нулевой;  q(1)= q(1×1)= q(1) q(1), следовательно, q(1)=1.

Легко проверить, что каждая из следующих функций

q(x)=1, q(x)= x, q(x)= x-1,

вполне мультипликативна.

Следующая теорема позволяет существенно расширить запас вполне мультипликативных функций.

Теорема. Произведение вполне мультипликативных функций является вполне мультипликативной функцией.

Доказательство. Пусть числа x и y взаимно просты, а функции f и g вполне мультипликативны. Тогда, обозначив через h произведение функций f и g, имеем:

h(xy)=f(xy)g(xy)=f(x)f(y)g(x)g(y)=[f(x)g(x)][f(y)g(y)]=

=h(x)h(y).

Следствие. Для любого целого k функция q(x)= xk  вполне мультипликативна.

20. Сумма значений функции по всем делителям аргумента.

Введем в рассмотрение, наряду с функцией  q(x), функцию

,

равную сумме всех значений функции q(d) при условии, что переменная d пробегает все делители числа x.

Теорема (основное тождество). Если x=, то

×.

В частности, если функция q вполне мультипликативна, то и функция  также вполне мультипликативна.

Доказательство. Рассмотрим произведение сумм, находящееся в правой части требуемого равенства:

=

==.

Осталось заметить, что для каждого набора (g1, g2,..., gk ) целых неотрицательных чисел gi, не превосходящих ai, в сумме

каждое слагаемое встречается ровно один раз. Учитывая теперь, что каждый делитель числа имеет вид , получаем

=.

Свойство полной мультипликативности рассматриваемой функции немедленно вытекает из того, что взаимно простые числа содержат различные простые сомножители. ÿ

30. Число делителей t(x) и сумма делителей s(x).

Рассмотрим следующие вполне мультипликативные функции:

t(x)= , где q(x)=1, - число делителей числа x,

s(x)= , где q(x) = x, - сумма делителей числа x.

Теорема. Справедливы тождества:

t()=(a1 + 1)( a2 + 1)...( ak + 1),

s()=.

Доказательство. а) Из определения функции t(x) немедленно следует указанное тождество, поскольку в силу основного тождества легко подсчитать число слагаемых, каждое из которых равно 1, в каждой из скобок соответствующего произведения.

б) Это тождество получается из основного тождества и формулы суммы членов геометрической прогрессии:

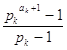.ÿ

40. Функция Эйлера. Одной из важнейших числовых функций является следующая функция, впервые введенная в рассмотрение Эйлером.

Определение. Через j(x) обозначается количество чисел ряда

1, 2, ..., x,                                   (*)

взаимно простых с числом x.

Справедлива следующая теорема, которую приведем без доказательства.

Теорема. Если x=, то

j(x)= x× .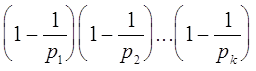

Следствие. Функция Эйлера вполне мультипликативна и

.

Теорема (тождество Гаусса). .

Доказательство. Применяя основное тождество и последнее следствие, получаем, считая  ,

 

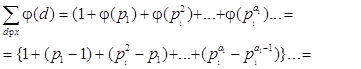
. ÿ

4. Алгоритм Евклида и его применения

10. Алгоритм Евклида. Наибольший общий делитель чисел a, b можно найти с помощью алгоритма Евклида, который состоит в следующем.

Пусть b>0. Разделим a на b, тогда по теореме о делении с остатком:

 a = bq1 + r1.

Если r1 = 0, то НОД(a, b) = b.

Если r1 ¹ 0, то разделим b с остатком на r1:

 b = r1q2 + r2.

Если r2 = 0, то процесс деления закончим, а если r2 ¹ 0, то разделим r1  с остатком на r2 :

 r1  = r2q3  + r3.

Продолжая далее таким же образом, мы закончим процесс деления как только получится остаток равный 0.

 Заметим, что такой остаток обязательно получится. В самом деле, остаток всегда меньше делителя,  поэтому b > r1 > r2  >  r3 > . . . и число получаемых остатков не превосходит b.

Итак, в результате указанного алгоритма получим, что:

	a  =  bq1  + r1 ,
	b  =  r1 q2  + r2 ,
	r1  =  r2 q3  + r3 ,	(1)
	. . . . . . . . . . . . .
	rn-2  =  rn-1 qn-1 + rn ,
	rn-1  =  rn qn .

Тогда на основании свойств 20 и 10 :

НОД(a, b) = НОД(b, r1) = НОД(r1, r2) = . . . = НОД(rn-1, rn) = rn.

Следовательно, наибольший общий делитель чисел a и b совпадает с последним ненулевым остатком rn  в алгоритме Евклида для  чисел a и b.

Пример. Найти НОД(160, 72).

Применим к данным числам алгоритм Евклида:

160 = 72×2 + 16,           72 = 16×4 + 8,             16 = 8×2.                                 (2)

Следовательно, НОД(160, 72) = 8.

20. Теорема (о линейном представлении  НОД). Если d - наибольший общий делитель чисел a и b, то существуют такие целые числа x и y, что выполняется равенство: d = xa + yb.

ð Допустим, что числа a и b связаны следующими соотношениями:

	a  =  bq1  + r1 ,
	b  =  r1 q2  + r2 ,
	r1  =  r2 q3  + r3 ,
	. . . . . . . . . . . . .
	rn-2  =  rn-1 qn-1 + rn .

Докажем, что каждое из чисел rk линейно выражается через a и b с целыми коэффициентами. Для r1 утверждение тривиально: r1 = a - bq1 . Считая, что каждое из чисел r1 , r2 , . . . , rn-1 является целочисленной линейной комбинацией чисел a и b (rk = ak a + bk b), имеем

rn = an-2 a + bn-2 b - (an-1 a + bn-1 b) qn-1 = (an-2 - an-1) a + (bn-2 - bn-1 qn-1)b. ð

Пример. Найти линейное представление НОД(160, 72).

Решение. Из второго равенства системы (2) следует, что 8 = 72 - 16×4, а из первого равенства получим, что 16 = 160 - 72×2. Из двух полученных равенств находим: 8 = 72 - 16 × 4 = 72 - (160 - 72 × 2) × 4 = (-4) × 160 + 9 × 72.

Таким образом, искомое представление НОД имеет вид:

8 = (-4) × 160 + 9 × 72.

30. Связь алгоритма Евклида с непрерывными дробями. Пусть a - рациональная несократимая дробь . Для разложения  числа a в непрерывную цепную дробь можно воспользоваться алгоритмом Евклида:

                     

               

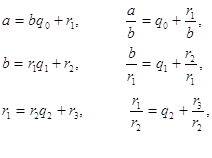
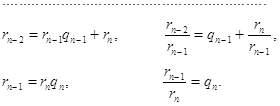
Следовательно, 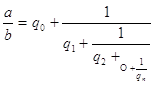       ,  откуда

Непрерывные дроби можно использовать для решения различных  теоретико-числовых задач.

1. Линейное представление наибольшего общего делителя

Пример 1. Найти линейное представление наибольшего общего делителя чисел (59, 163).

Решение. Разложим в непрерывную дробь число:

= [2; 1, 3, 4, 1, 2].

Cледовательно,  можно теперь заполнить таблицу:

qs	2	1	3	4	1	2
Ps	1	2	3	11	47	58	163
Qs	0	1	1	4	17	21	59
es	+1	-1	+1	-1	+1	-1

Отсюда получаем 59 × 58 - 163 × 21 = -1 или 59 × (-58) + 163 × 21 = 1.

2. Решение линейных диофантовых уравнений

Как практически находить какое-нибудь решение линейного неопределенного уравнения

ax + by = c     при  (a, b)=1, c=1 ?

Можно воспользоваться алгоритмом Евклида, из которого легко получить линейное представление НОД чисел  a, b, или представить дробь  в виде последней подходящей  , откуда aQn - bPn = (-1)n .

Пример. Решить диофантово уравнение 163x + 59y = 1.

Решение. Мы проверили раньше, что 163 × 21 + 59 × (-58) = 1, следовательно, общее решение имеет вид:

                                                

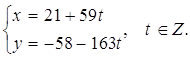
6. Базис и размерность векторного пространства

10. Линейные комбинации и линейные оболочки векторов. Выражение вида  = a1e1 + . . . + anen, где ai - числа, ei - векторы из пространства V, называется линейной комбинацией векторов ei; числа ai называются коэффициентами линейной комбинации.

Определение. Линейной оболочкой системы векторов E = (e1, . . . , en) называется множество всевозможных линейных комбинаций векторов данной системы; обозначение L(E). Таким образом,

Страницы: 1, 2, 3, 4