Реферат: Исследование операций
Предприятие 1 - Р(план) = 740 – y2 = 740 – 0 = 740 тыс. тонн,
Предприятие 2 – Р(план) = 680 – y3 = 680 – 575,88043 = 104,11957 тыс. тонн,
Предприятие 3 – Р(план) = 600 – y4 = 600 – 82,00002 = 517,99998 тыс. тонн.
Целочисленное линейное программирование.
При решении некоторых задач линейного программирования бывает необходимо получить целочисленное решение, которое находится методами целочисленного линейного программирования.
Задача целочисленного линейного программирования это задача, где некоторые или все переменные должны принимать строго целочисленные значения, а целевая функция и ограничения – линейные.
В некоторых задачах целочисленные значения могут быть равны только 0 или 1, тогда такие задачи называются задачами с булевыми переменными.
Задачу целочисленного линейного программирования можно решить как задачу линейного программирования, а затем округлить полученное решение. Однако такой способ допустим только при условии, что значения переменных настолько большие, что погрешностью, вызываемой округлением можно пренебречь. Если же в результате решения переменная принимает малое значение, то ее округление может привести к очень далекому от оптимального решения. Применяются два способа решения задач ЦЛП – метод отсечений и метод ветвей и границ.
Решение задачи ЦЛП методом отсечения:
1. Решение задачи как задачи ЛП.
2. Если мы получили целочисленное решение, то оно и является решением задачи ЦЛП.
3. Если мы получаем нецелочисленное решение, то мы к системе ограничений задачи ЛП прибавляем такое ограничение, что полученное нецелочисленное оптимальное решение не может содержаться во множестве допустимых решений и, таким образом, формируем новую задачу ЛП и решаем ее. Цикл повторяется до тех пор пока не будет получено целочисленное решение (решение задачи ЦЛП (если оно существует)).
Решение задачи ЦЛП методом ветвей и границ:
1. Решаем задачу как задачу ЛП.
2. Если мы получим оптимальные целочисленные решения задачи ЛП, то они являются также и оптимальными решениями задачи ЦЛП.
3. Если мы не получим целочисленных решений, то целевая функция Z1 задачи ЛП становится верхней границей оптимального значения Z задачи ЦЛП, потому что значение целевой функции Z при введении в дальнейшем новых ограничений для получения оптимальных целочисленных решений уменьшается.
4.
Затем производится ветвление по
одному из нецелочисленных оптимальных решений задачи ЛП. Ветвление
осуществляется с использованием некоторых правил по следующей схеме: если
n
x
n+1, то 1)
x
n; 2) x
n+1, где х – нецелочисленное оптимальное решение задачи
ЛП, по которому мы осуществляем ветвление, n – ближайшее целое к х не превышающее х.
Правила ветвления:
1) Выбирается переменная, у которой дробная часть наиболее близка к 0,5.
2) Выбирается переменная с наибольшим приоритетом по какому — либо качественному или количественному значению.
3) Переменная выбирается произвольно.
Ограничения введенные при ветвлении добавляются к ограничениям задачи ЛП.
В каждой из вершин находим оптимальные решения полученных путем добавления новых ограничений задач ЛП – 2 и ЛП – 3. Если не у одной из них мы не получили целочисленных оптимальных решений, то мы выбираем ту вершину, в которой получено наибольшее значение целевой функции и производим дальнейшее ветвление. Так продолжается до получения целочисленного оптимального решения одной из задач ЛП.
Вершина называется прозондированной, если:
1) Мы нашли в ней оптимальное целочисленное решение – решение задачи ЦЛП.
2) В данной вершине нет оптимальных решений задачи ЛП.
3) Значение Z в оптимальном решении задачи ЛП не больше текущей нижней границы.
Прочие вершины называются висящими.
Решение задачи методом целочисленного линейного программирования.
Метод ветвей и границ.
Начальные условия берутся из решения задачи ЛП (решение см. выше).
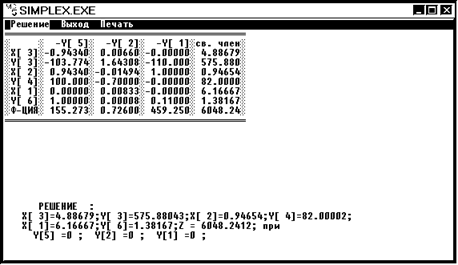
1. Вершина 1 x1 = 6,17 x2 = 0,9 x3 = 4,9 Z1 = 6048,24
Начнем
ветвление по x1 =
6,17, тогда получаем дополнительные
ограничения а) x1 
6 (1 ветвь) б) x2 
7 (2 ветвь).
Решаем сначала ветвь 1. К ограничениям задачи ЛП добавляем ограничение а.
Получаем седьмым ограничением ограничение x1
6;
Решение:
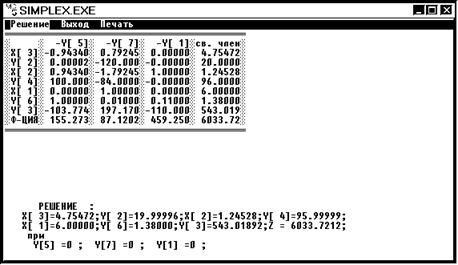
2. Вершина 2 x1 = 6 x2 = 1,2 x3 = 4,8 Z2 = 6033,7212
Мы получили одно целочисленное решение x1 = 6, следовательно дальнейшее ветвление мы будем проводить по x2 или x3.
Решаем ветвь 2. К ограничениям задачи ЛП добавляем ограничение б.
Седьмым
ограничением становится ограничение x1 
7.
Решение:
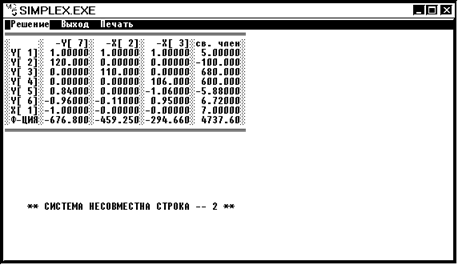
Второй строкой является ограничение задачи ЛП по максимально возможному объему руды с 2 предприятия:
120x1 
740 или x1
6,16666, что противоречит введенному нами условию 6 (б) x1 
7.
Дальнейшее ветвление из вершины 3
невозможно.
Продолжим ветвление из вершины 2. Как
было уже сказано выше, мы можем продолжить ветвление по x2 или x3.
Продолжим ветвление по x2. x2 = 1,2, следовательно восьмое ограничение для 1 ветви будет x2 
1, а
для другой x2
. Движемся сначала по ветви 1 в вершину 4.
Решение:
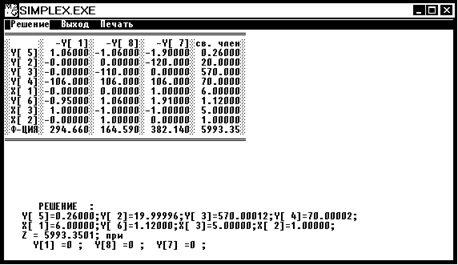
X1 = 6 x2
= 1 x3 = 5 Z4 = 5993,3501
Мы получили, что все три переменных имеют целочисленное значение,
но, чтобы данное решение являлось решением задачи ЦЛП необходимо и достаточно показать, что при ветвлении по ветви 2 в вершине 5 мы получим значение целевой функции Z5 < Z4. Найдем решение в вершине 5.
Решение:
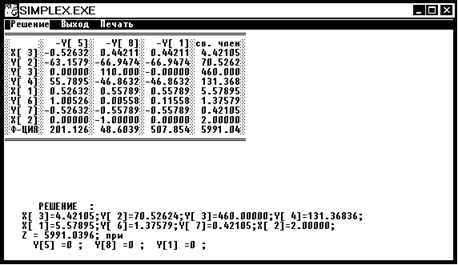
Z5 = 5991,0396, следовательно Z5 < Z4, значит в вершине 4 мы получили решение задачи ЦЛП.
Интерпретация решения с помощью блок – схемы:
x1=6,1
Z1=6048 x2=0,9
x3=4,9
x1
6
x1
7
x1=6
x2=1,2 Система
x3=4,8 несовместна
 |
 |
x2
1
x2
2
x1=6
x1=5,6
x2=1 x2=2
x3=5 x3=4
Z=5993 Z=5991
| Вершина | Ограничение | № ограничения |
| 2 |
x1 |
7 |
| 3 |
x1 |
7 |
| 4 |
x1 x2 |
7 8 |
| 5 |
x1 x2 |
7 8 |
6
7
6
1
6
2
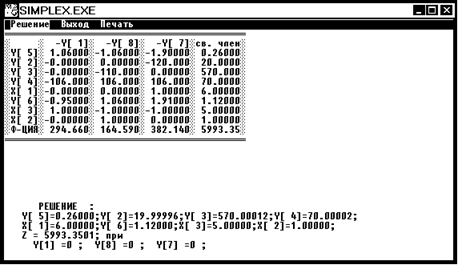
Вывод:
В результате решения я получил, что целочисленное оптимальное решение получается в вершине 4, так как все значения x1=6, x2=1,x3=5 в этой вершине целочисленные и Z5(5991)<Z4(5993), следовательно получено оптимальное решение. Висящая вершина 5 и прозондированные 1,2,3,4.
Плановые задания:
, где P – плановое
задание тыс. тонн, q – производительность состава, x – количество составов, i –
номер предприятия.
Для предприятия 1:
тыс. тонн;
Для предприятия 2:
тыс. тонн;
Для предприятия 3:
тыс. тонн.
Нелинейное программирование.
Задача математического программирования называется нелинейной, если нелинейны ограничения или целевая функция.
Задачи нелинейного программирования бывают выпуклого и невыпуклого программирования, с ограничениями и без ограничений, с квадратичными или сепарабельными целевыми функциями. Задачи нелинейного программирования имеют множество экстремальных точек, и сложность решения заключается в выделении глобального оптимума, а не локального как это делается в большинстве классических методов.
Разделяют задачи безусловной и условной оптимизации. Задачами безусловной оптимизации называются задачи оптимизации функции многих переменных без дополнительных ограничений. Существуют следующие методы безусловной оптимизации: покоординатного спуска, градиентные, сопряженных направлений, метод Ньютона. Задачами условной оптимизации называются задачи о оптимизации целевой функции многих переменных f(x1, …, xn) при условии, что эти переменные удовлетворяют следующим ограничениям:
qi(x1,
…, xn) = 0, 
или
dj(x1, …, xn) 
0, 
Решение задачи основывается на линейной или квадратичной аппроксимации целевой функции для определения приращений x1, …,xn на каждой итерации.
Существуют также приближенные методы решения нелинейных задач. Это методы основанные на методе кусочно-линейной аппроксимации. Точность нахождения решений зависит от количества интервалов, на которых мы находим решение линейной задачи, максимально приближенной к нелинейной. Такой метод позволяет производить расчеты с помощью симплекс-метода. Обычно в линейных моделях коэффициенты целевой функции постоянны и не зависят от значения переменных. Однако существует ряд задач, где затраты зависят от объема нелинейно. Такие задачи решаются следующим способом: решают задачу ЛП с коэффициентами целевой функции при максимальных значениях переменных. Если в решении мы получили переменные, для которых брались коэффициенты, значит задача решена. В противном случае мы изменяем коэффициенты при целевой функции на коэффициенты при вновь полученных значениях переменных и решаем полученную задачу ЛП. Так мы повторяем до тех пор, пока не будет получено на двух последующих шагах одно и то же решение.
Решение задачи нелинейного программирования.
Метод кусочно – линейной аппроксимации.
В нашей задаче есть такая величина, как коэффициент увеличения затрат при нагрузке, который не использовался нами при решении задачи методами ЛП и ЦЛП. Собственно этот коэффициент и введен для превращения задачи в нелинейную путем нелинейной зависимости между увеличением затрат и загрузкой предприятий.
Составим таблицу:
| № предприятия |
Коэффи- Циент затрат % |
Количе-ство составов |
Коэфф. измене-ния затрат |
Затраты на 1т у.е. | Доход |
Прибыль На 1т у.е. |
Прибыль на 1 состав у.е. |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Π| 100 | 6,17 | 1 | 6 | 11,64 | 5,64 | 676,8 |
| 70 – 100 | 4.31–6,16 | 1,4 | 8,4 | 3,24 | 388,8 | ||
| 50 – 70 | 3,08–4,31 | 1,6 | 9,6 | 2,04 | 244,8 | ||
| 30 – 50 | 1,85–3,08 | 1,7 | 10,2 | 1,44 | 172,8 | ||
| до 30 | до 1,85 | 1,8 | 10,8 | 0,84 | 100,8 | ||
| | 100 | 6,18 | 1 | 7 | 11,175 | 4,175 | 459,25 |
| 70 – 100 | 4,33-6,18 | 1,2 | 8,4 | 2,775 | 305,25 | ||
| 50 – 70 | 3,09-4,33 | 1,4 | 9,8 | 1,375 | 151,25 | ||
| 30 – 50 | 1,85-3,09 | 1,5 | 10,5 | 0,675 | 74,25 | ||
| до 30 | до 1,85 | 1,7 | 11,9 | - 0,725 | - 79,75 | ||
| Ž | 100 | 5,66 | 1 | 8 | 10,78 | 2,78 | 294,66 |
| 70 – 100 | 3,96-5,66 | 1,3 | 10,4 | 0,38 | 40,28 | ||
| 50 – 70 | 2,83-3,96 | 1,6 | 12,8 | - 2,02 | - 214,12 | ||
| 30 – 50 | 1,7 – 2,83 | 1,7 | 13,6 | - 2,82 | - 298,92 | ||
| до 30 | до 1,7 | 1,9 | 15,2 | - 4,42 | - 458,52 |
Где доход (Д) рассчитывается по формуле:
