Курсовая работа: Анализ методов определения минимального, максимального значения функции при наличии ограничений

Геометрически, эти условия означают, что, во-первых, вектор h является касательным к многообразию, выделяемому ограничениями-равенствами (т. е. ортогонален всем градиентам f ¢i(x)), и, во-вторых, он образует с градиентами g¢j(x) активных ограничений (указывающими, очевидно, вовне множества W) тупой угол.

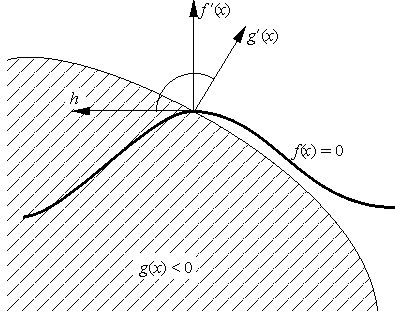
Рис. 3.3.

Методы возможных направлений

Эти методы основываются на следующем простом понятии. Вектор (направление) z в допустимой точке x назовем возможным для задачи (3.1), (3.3), если малое перемещение в этом направлении уменьшает значение функции f0 и не выводит из множества допустимых точек, т. е. если при достаточно малых s точка xs = x + sz допустима и f(xs) < f(x). Если теперь на каждом шаге сдвигаться в возможном направлении на достаточно малое расстояние, то мы очевидно получим релаксационную последовательность, которая во многих случаях будет сходиться к решению задачи. Методы этого типа называются методами возможных направлений.

Методы проекции градиента

Проекцией PWx точки x Î Rm на множество W Ì Rm называется любая ближайшая к x точка множества W:

||x  PWx|| £ ||x  y|| при всех y Î W.

В тех случаях, когда проекцию точки на множество допустимых точек задачи (3.1), (3.3) найти достаточно легко (например, когда  — линейное подпространство, полупространство, шар, Rm и т. д.) используют метод проекции градиента:

xn+1 = PW(xn  anf ¢0(xn))

(см. рис. 3.4), являющийся прямым обобщением градиентного метода.

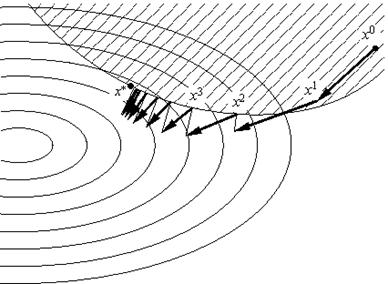
Рис. 3.4.

Можно доказать, например, что если функция f0 Î C1 сильно выпукла и f ¢ удовлетворяет условию Липшица, а множество W замкнуто и ограничено, то метод проекции градиента сходится со скоростью геометрической прогрессии.

Методы линеаризации

Суть этих методов, как следует из названия, состоит в линеаризации минимизируемой функции и ограничений в очередной точке xn строящейся релаксационной последовательности и объявлении следующим значением xn+1 решения получающейся линейной задачи, т. е. задачи

(f ¢0(xn),x  xn) ® min, (3.8)

gi(xn) + (g¢i(xn),x  xn) £ 0, i = 1, ..., l. (3.9)

Чтобы эта (линейная) задача была разрешима либо добавляют штраф в минимизируемую функцию, заменяя (3.8), например, задачей

(f ¢0(xn), x xn) + d||x  xn||2 ® min,

либо добавляя к (3.9) простые ограничения, которые делают множество допустимых точек этой задачи ограниченным, например, (линейные) ограничения

xi  xni an £ 0, xi + xni an £ 0 (i = 1, ..., m).

 

Методы штрафов

Основная идея здесь заключается в переходе от задачи (3.1), (3.3) к задаче безусловной оптимизации, в которой "наказывается" либо удаление от множества W допустимых точек (внешний штраф), либо приближение изнутри множества W к его границе (внутренний штраф). Различают методы внешних штрафов и внутренних штрафов. При методе внешних штрафов задачу решают тем или иным методом решения безусловных задач, увеличивая на каждом шаге штраф s. Как и в случае задач с ограничениями-равенствами, основным недостатком метода штрафов является рост числа обусловленности s. На несколько другой идее основываются так называемые методы внутренних штрафов или барьеров. Образно его можно описать так: у границы множества W возводятся барьеры, не позволяющие приближаться к его границе.

Ни один метод или класс методов не выделяется своей собственной высокой эффективностью при решении оптимизационных задач различных типов, т.е. универсальностью.

Симплекс - метод

Симплекс-метод – один из наиболее эффективных методов численного решения задач ЛП. Суть понятия "симплекс" заключается в следующем. Для тела в k-мерном пространстве симплексом называется множество, состоящее из k+1 вершин этого тела. Так, при k = 2, т.е. на плоскости, симплексом будут вершины треугольника; при k = 3 симплексом являются вершины четырехгранника, например тетраэдра, и т.д. Такое название методу дано по той причине, что в его основе лежит последовательный перебор вершин ОДЗП с целью определения координат той вершины, в которой функция цели имеет экстремальное значение.

Решение задачи с помощью симплекс-метода разбивается на два основных этапа. На первом этапе находят одно из решений, удовлетворяющее системе ограничений. Системы, в которых переменных больше, чем ограничений N > m, называются неопределенными. Они приводятся к определенным системам (N = m) путем приравнивания к нулю N-m каких-либо переменных.

При этом остается система m уравнений с m неизвестными, которая имеет решение, если определитель системы отличен от нуля. В симплекс-методе вводится понятие базисных переменных, или базиса. Базисом называется любой набор из m таких переменных, что определитель, составленный из коэффициентов при этих переменных в m-ограничениях, отличен от нуля. Остальные N-m переменных называются небазисными или свободными переменными.

Если принять, что все небазисные переменные равны нулю, и решать систему ограничений относительно базисных переменных, то получим базисное решение.

В системе из m уравнений с N неизвестными общее число базисных решений при N > m определяется числом сочетаний

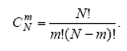
Базисное решение, в котором все xi ≥ 0, i = [1,m], называется допустимым базисным решением. Таким образом, первый этап завершается нахождением допустимого базисного решения, хотя бы и неудачного.

На втором этапе производится последовательное улучшение найденного решения. При этом осуществляется переход от одного допустимого базисного решения к другому таким образом, чтобы значение целевой функции улучшилось. Процесс продолжается до тех пор, пока не будет достигнуто наименьшее (или наибольшее) значение функции цели. Геометрически это означает переход по ребрам из одной вершины многогранника допустимых значений в другую по направлению к той, в которой значение функции цели достигает экстремума. Симплекс-метод дает оптимальную процедуру перебора базисных решений и обеспечивает сходимость к экстремальной точке за конечное число шагов. Вычисления на втором этапе ведутся по следующей схеме:

·  базисные переменные и функция цели выражаются через небазисные переменные;

·  по определенному правилу выбирается та из небазисных переменных, изменение значения которой способно улучшить значение F(x) , и она вводится в базис;

·  определяется, какая из базисных переменных должна быть выведена из базиса, при этом новый набор базисных переменных, образующийся на каждом шаге, отличается от предыдущего только одной переменной;

·  базисные переменные и функция цели выражаются через новые небазисные переменные, и повторяются операции 2 и 3.

Если на определенном шаге окажется, что изменение значений любой из небазисных переменных не может улучшить F(x) , то последнее базисное решение оказывается оптимальным.

4. Нахождение экстремума функции при наличии ограничений

Метод симплексных процедур

Симплексом в пространстве n-измерений называют выпуклый многогранник, имеющий n+1 вершин, не лежащих в подпространстве размерности, меньшей n.

Решение задачи нахождения условного экстремума функции двух переменных может находиться либо на границах выпуклого многогранника, либо на его вершинах.

Согласно методу симплексных процедур экстремум функции обязательно лежит среди допустимых базисных решений. Это позволяет наметить путь к решению задачи, число которых конечно, а также найти все допустимые базисные решения и для каждого вычислить значение целевой функции, а затем выбрать из них min/max, хотя данный метод достаточно трудоемок.

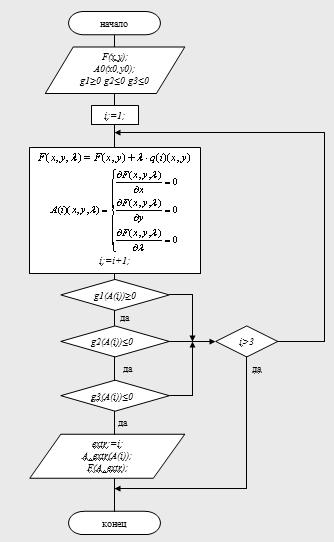
Рис. 4.1. Блок-схема метода симплексных процедур.

 

Реализация метода в программе:

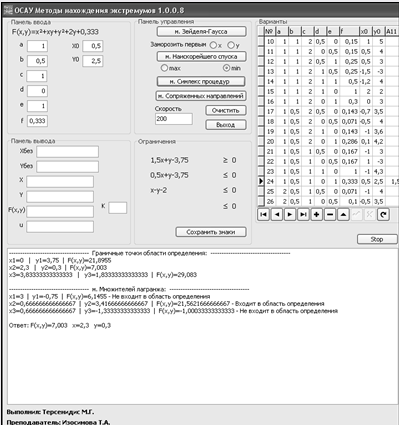
Рис. 4.2. Реализация метода симплексных процедур.

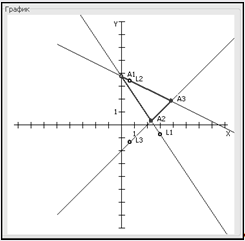
Рис. 4.3. График метода симплексных процедур.

Вывод: Минимальное значение функция принимает в точке А2 (2.3, 0.3). F(2.3, 0.3) = 7,003.

5. Синтез оптимальной по быстродействию системы с помощью принципа максимума Понтрягина

 

Синтез системы

Критерий управления, как отмечалось ранее, в этом случае

Мера ошибки в критерии H =1, а верхний предел T неизвестен. Начальная Х(0) = Х0 и конечная Х(T) = ХT точки закреплены.

Запишем функцию Гамильтона и условия трансверсальности:

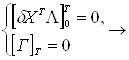
 (T) и  (0)-произвольны.

Согласно принципу максимума Понтрягина, стратегия управления состоит в минимизации функции Гамильтона относительно u. Минимум Г будет тогда, когда  min по и или  min по и

Отсюда

 (5.2)

Таким образом, стратегия управления и характер u*(t) определены: оптимальное управление - это релейное управление, максимальное по величине, причем переключение управления производится тогда, когда функция ТВ пересекает ось времени t.

По изложенной методике определим оптимальное управление , которое произвольное начальное состояние (х10, x20) переводит в начало координат за минимальное время Т.

Представим объект  (5.1) в виде уравнения состояния (нормальная форма)

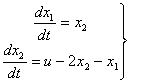 (5.3)

В рассматриваемом примере матрица , вектор . Образуем матрицу .

Матрица G — невырожденная, поэтому система (3) будет нормальной. Характеристические числа матрицы A  = 0,  = -2, это числа вещественные, поэтому система (3) удовлетворяет условиям теоремы об n-интервалах. Оптимальное управление u*(t) является кусочно-постоянным и имеет не более двух интервалов постоянства.

Таким образом, управляющие последовательности в зависимости от начального состояния будут: {+ 1}, {-1},{+1,-1}, {-1, + 1}.

Обозначим u* = ∆=±1 и найдем общее решение системы при и* = ∆.

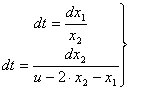
Обозначим  – множество начальных состояний, которые переводятся в начало координат управляющей последовательностью и* = {+1}, – множество начальных состояний, которые переводятся в начало координат управляющей последовательностью и* = {-1}. Эти множества описываются уравнениями

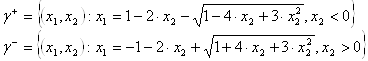
Если принять  то множество  запишется в виде

Закон управления

 (5.4)

Линия  представляет собой линию переключения.

Введем функцию , характеризующую расстояние от текущего положения фазовой точки (x1,x2) до линии переключения:

 (5.5)

Когда фазовая точка окажется на линии переключения, то правая часть уравнения (5) будет равна нулю ( = 0) и управляющее устройство должно произвести переключение знака управления на противоположный. Пока фазовая точка находится над линией переключения,  > 0 и управление должно быть отрицательным и (t) = -U. Когда фазовая точка находится под линией переключения,  < 0 и управление должно быть положительным и (t) = +U. Таким образом, в зависимости от знака должен выбираться и знак управления:

Все изложенное позволяет записать алгоритм оптимального по быстродействию регулятора для объекта (1):

=0, если , х2

По алгоритму решения составим структурную схему системы, реализующей закон управления

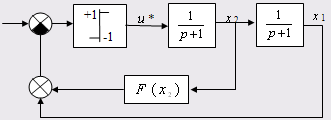
Рис. 5.1. Структурная схема системы

Моделирование объекта

По алгоритму решения

,

полученному ранее, составим структурные схемы для построения переходной и импульсной характеристик системы, реализующие закон управления для объекта , где k = 1, T1 = 10, T2 = 8.

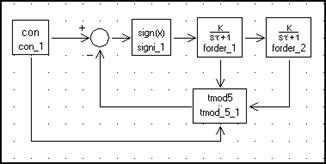
Рис. 5.2. Структурная схема модели ОСАУ для переходной характеристики

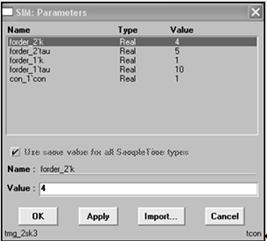
Рис. 5.3. Вводимые параметры

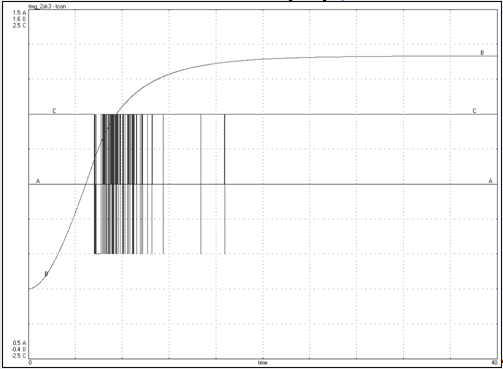
Рис. 5.4. График переходной характеристики

tp = 31.6 c.

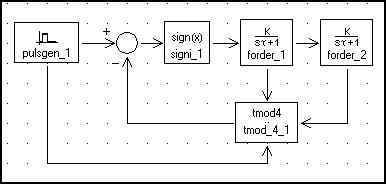
Рис. 5.5. Структурная схема модели ОСАУ для импульсной характеристики

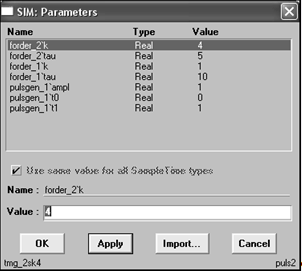
Рис. 5.6. Вводимые параметры

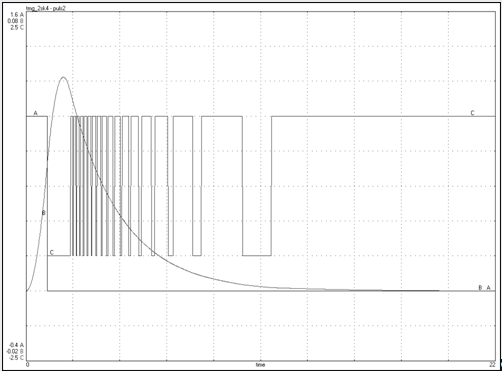
Рис. 5.7. График импульсной характеристики

tp = 19,6 c.

Заключение

В теоретической части курсового проекта были рассмотрены методы поиска безусловного экстремума функции (методы прямого поиска, градиентные методы, методы второго порядка) и методы поиска экстремума функции при наличии ограничений (методы возможных направлений, методы проекции градиента, методы линеаризации, методы штрафов), указаны их основные достоинства и недостатки.

Страницы: 1, 2, 3, 4, 5