Курсовая работа: Анализ методов определения минимального, максимального значения функции при наличии ограничений

·  из необходимых условий нельзя определить, глобальный это экстремум или локальный.

Поэтому, когда находят точки подозрительные на exst, их дополнительно исследуют, например, на основе определения exst или 2-ой производной.

Метод наискорейшего спуска

Метод наискорейшего спуска является градиентным методом с переменным шагом. На каждой итерации величина шага ak выбирается из условия минимума функции f(x) в направлении спуска, т.е.

.

Это условие означает, что движение вдоль антиградиента происходит до тех пор, пока значение функции f (x) убывает. С математической точки зрения на каждой итерации необходимо решать задачу одномерной минимизации по a функции

j (a)=f (x(k)-aÑf (x(k)))

Воспользуемся для этого методом золотого сечения.

Алгоритм метода наискорейшего спуска состоит в следующем.

1.  Задаются координаты начальной точки x(0).

2.  В точке x(k), k = 0, 1, 2, …, вычисляется значение градиентаÑf (x(k)).

3.  Определяется величина шага ak путем одномерной минимизации по a функции

j (a)=f (x(k)-aÑf (x(k))).

4.  Определяются координаты точки x(k):

xi(k+1)= xi(k)-akÑfi (x(k)), i=1, …, n.

5.  Проверяется условие останова итерационного процесса:

||Ñf (x(k+1))||£e .

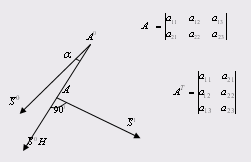
Если оно выполняется, то вычисления прекращаются. В противном случае осуществляется переход к п. 1. Геометрическая интерпретация метода наискорейшего спуска представлена на рис. 1.

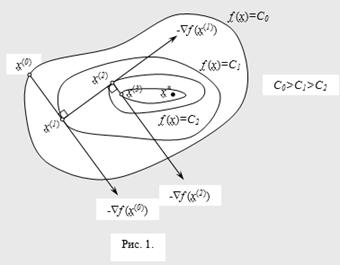
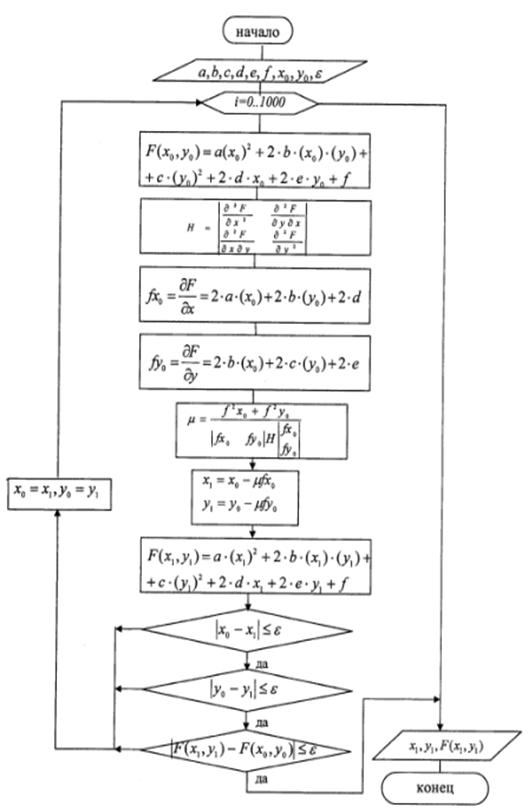
Рис. 2.1. Блок схема метода наискорейшего спуска.

Реализация метода в программе:

Метод наискорейшего спуска.

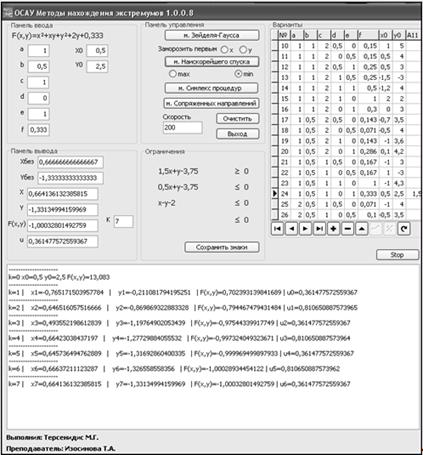
Рис. 2.2. Реализация метода наискорейшего спуска.

Вывод: В нашем случае метод сошёлся за 7 итераций. Точка А7 (0,6641; -1,3313) является точкой экстремума. Метод сопряженных направлений. Для квадратичных функций можно создать градиентный метод, при котором время сходимости будет конечным и равно числу переменных n.

Назовем некоторое направление  и  сопряженными по отношению к некоторой положительно определенной матрице Гесса H, если выполняется:

 Если ,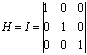

Тогда  т.е. . Значит при единичной H, сопряженное направление означает их перпендикуляр. В общем же случае H неединичная. В общем случае сопряженность - это применение матрицы Гесса к вектору  - означает поворот этого вектора на некоторый угол  и его растяжение или сжатие.

А теперь вектору  вектор  ортогонален т. е. сопряженность это не ортогональность векторов  и , а ортогональность повернутого вектора  т.е.  и .

Рис. 2.3. Блок-схема метода сопряженных направлений.

Реализация метода в программе: Метод сопряженных направлений.

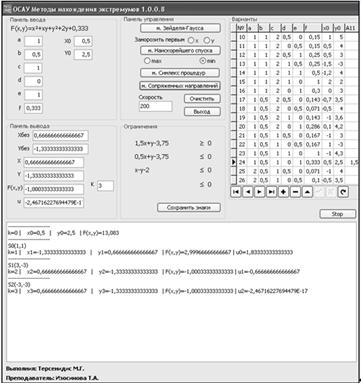
Рис. 2.4. Реализация метода сопряженных направлений.

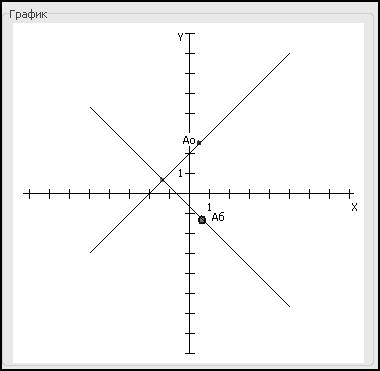
Рис. 2.5. График метода сопряженных направлений.

Вывод: Точка А3 (0,6666; -1,3333), была найдена за 3 итерации и является точкой экстремума.

3. Анализ методов определения минимального, максимального значения функции при наличии ограничений

Напомним, что общая задача условной оптимизации выглядит так

f(x) ® min, x Î W,

где W — собственное подмножество Rm. Подкласс задач с ограничениями типа равенств выделяется тем, что множество  задается ограничениями вида

fi(x) = 0, где fi: Rm ®R (i = 1, …, k).

Таким образом,W = {x Î Rm: fi(x) = 0, i = 1, …, k}.

Нам будет удобно писать у функции f индекс "0". Таким образом, задача оптимизации с ограничениями типа равенств записывается в виде

f0(x) ® min, (3.1)

fi(x) = 0, i = 1, …, k. (3.2)

Если обозначить теперь через f функцию на Rm со значениями в Rk, координатная запись которой имеет вид f(x) = (f1(x), …, fk(x)), то (3.1)–(3.2) можно также записать в виде

f0(x) ® min, f(x) = Q.

Геометрически задача с ограничениями типа равенств — это задача о поиске наинизшей точки графика функции f0 над многообразием  (см. рис. 3.1).

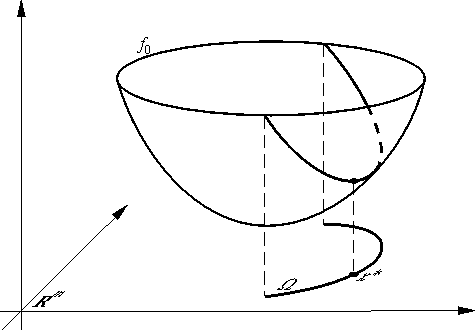
Рис. 3.1.

Точки, удовлетворяющие всем ограничениям (т. е. точки множества ), обычно называют допустимыми. Допустимая точка x* называется условным минимумом функции f0 при ограничениях fi(x) = 0, i = 1, ..., k (или решением задачи (3.1)–(3.2)), если при всех допустимых точках x f0(x*)  f0(x). (3.3)

Если (3.3) выполняется только для допустимых x, лежащих в некоторой окрестности Vx* точки x*, то говорят о локальном условном минимуме. Естественным образом определяются понятия условных строгих локального и глобального минимумов.

Правило множителей Лагранжа

Описываемый ниже необходимый признак локального условного минимума был сформулирован Лагранжем. Определим F: Rm ® Rk+1, положив F(x) = (f0(x), f1(x), ..., fk(x)). Заданная на Rm×Rk+1 скалярная функция Лагранжа M по определению принимает значения в R и задается равенством

M(x, m) = (m, F(x)) =  mi fi(x) (x Î Rm, m Î Rk+1).

Координаты вектора m, т. е. числа m0, m1, ..., mk называются множителями Лагранжа или двойственными переменными. Оказывается, имеет место следующая теорема, часто именуемая правилом множителей Лагранжа:

Теорема. Пусть F Î C1 и x* — локальный условный минимум функции f0 при ограничениях fi(x) = 0 (i = 1, ..., k). Тогда найдется ненулевой вектор m* такой, что x* является стационарной точкой функции x M(x, *):

M¢x(x, m*)|x=x*=m*i f ¢i(x*)= Q.

Правило множителей Лагранжа доставляет необходимое условие локального условного минимума и поэтому позволяет искать точки, "подозрительные" на экстремум. В самом деле, для нахождения точки (x*, m*) Î Rm+k+1, т. е. для нахождения m + k + 1 неизвестных, мы имеем m + k уравнений

f(x) = Q, M¢x(x, l)= Q.

Поскольку, очевидно, множители Лагранжа можно искать с точностью до постоянного множителя, то в общей ситуации этих уравнений хватает для отыскания x*.

Регулярные точки

Допустимая точка x задачи (3.1)–(3.2) называется регулярной, если векторы {f i(x)}ki=1линейно независимы. Оказывается, что если x* — регулярная точка минимума, то в векторе * можно считать *0 ненулевым, а поскольку множители Лагранжа определяются с точностью до множителя, можно считать, что *0 = 1. Чтобы сформулировать это утверждение более точно, введем следующие обозначения. Пусть   Rk, а функция Лагранжа в регулярном случае определяется равенством

L(x, l) = f0(x) + (l, f(x)) = f0(x) + li fi(x) (x Î Rm, l Î Rk).

Очевидно, L(x, l) = M(x, m), где m = (1, l).

Теорема (правило множителей Лагранжа в регулярном случае)

Пусть F  C1, а x* — регулярное локальное решение задачи (3.1)–(3.2). Тогда найдется ненулевой вектор *  Rk такой, что

L¢x(x*, l*)= Q.

Одно достаточное условие локального минимума

Говорят, что линейный оператор A положительно определен на подпространстве E, если (Ax, x) > 0 при всех x  E. Касательным подпространством к многообразию  в точке y называется множество Ty = {x  Rm: (f (y), x) = 0, i = 1, ..., k}. Касательной гиперплоскостью к многообразию  в точке y называется множество

W¢y = {x Î Rm: fi(y) + (f ¢(y), xy) = 0, i = 1, ..., k}.

Теорема (достаточное условие минимума)

Пусть F Î C2, а x* — регулярная стационарная точка функции Лагранжа, т. е., в частности, L¢(x*, *) =  при некотором ненулевом *  Rk. Тогда, если Lxx¢¢(x*, l*)положительно определен на Tx*, то точка x* является локальным решением задачи (3.1)–(3.2).

Методы решения задач с ограничениями типа равенств

Мы будем рассматривать ниже только регулярный случай. Один из естественных подходов к решению задач типа (3.1)–(3.2) основывается на необходимом условии экстремума — правиле множителей Лагранжа. Если бы можно было утверждать, что решению x* задачи (3.1)–(3.2) соответствует экстремум (x*, *) функции Лагранжа L, то к функции L можно было бы применять разработанные методы решения безусловных задач. Однако, так утверждать нельзя. В самом деле, если в точке x ограничения не выполняются, то за счет выбора  функцию L (поскольку по  она линейна) можно сделать как сколь угодно большой положительной, так и сколь угодно большой отрицательной. Поэтому естественно искать решение x* как первые m координат стационарной точки функции Лагранжа, например, методом Ньютона, мы приходим к методу Ньютона решения задач с ограничениями типа равенств — это просто метод Ньютона решения уравнения L(x, ) =  (в регулярном случае):

L¢(xn, ln) + L¢¢(xn, ln)(xn+1  xn, ln+1 - ln) = Q

в "координатной" форме

L¢x(xn,ln) + L¢¢xx(xn,ln)(xn+1 - xn) + L¢¢xl(xn,ln)(ln+1 - ln) = Q,

L¢l(xn,ln) + L¢¢xl(xn,ln)(xn+1 - xn) + L¢¢ll(xn,ln)(ln+1 - ln) = Q.

Остается подставить в эти уравнения явные выражения производных функции Лагранжа (учитывая, в частности, что L¢¢ll(xn,ln) = Q):

f ¢0(xn)+ [f ¢(xn)]*ln + (f ¢¢0(xn)+ lnif ¢¢i(xn)) (xn+1  xn) + [f ¢(xn)]*(ln+1  ln) = Q,

f(xn) + f ¢(xn)(xn+1  xn) = Q

и мы получаем m+k линейных уравнений для нахождения m+k неизвестных (xn+1, ln+1).

Описанный метод обладает всеми достоинствами и всеми недостатками метода Ньютона решения безусловных задач, в частности, он лишь локально сходится и требует большого объема вычислений. Поэтому попытаемся модифицировать градиентный метод, приспособив его к решению условной задачи (3.1)–(3.2). Поскольку, как сказано выше, точка (x*, *) - это седловая точка функции Лагранжа, то естественно пытаться с помощью градиентного метода минимизировать ее по x, одновременно максимизируя ее по :

xn+1 = xn  aL¢x(xn,ln), ln+1 = ln + aL¢l(xn,ln),

или, что то же xn+1 = xn  a(f ¢0(xn)+ [f ¢(xn)]*ln), ln+1 = ln + af(xn).

Можно доказать, что этот метод (его обычно называют методом Эрроу — Гурвица) при естественных ограничениях на гладкость и при условии положительной определенности оператора L¢¢xx(x*,l*) локально линейно сходится.

Описанные методы относятся к разряду двойственных методов, поскольку в итерационном процессе участвуют как прямые (x), так и двойственные (l) переменные.

Можно строить также прямые методы решения условных задач. Например, реализовать идею о том, что следующее приближение градиентного метода. Приближение xn+1 ищется как минимум функции x ® (f ¢0(xn),x  xn) + a||x  xn||2 на касательной гиперплоскости W¢xn. Здесь "штрафной член" ||x  xn||2 позволяет "минимизировать" линейную функцию x ® (f ¢0(xn),x  xn). Таким образом, мы приходим к прямому методу

xn+1 = argmin [(f ¢0(xn),x  xn) + a||x  xn||2], (3.4)

fi(xn) + (f ¢i(xn),x  xn) = 0, i = 1, ..., k. (3.5)

Ограничения (3.5) в этом методе — это, очевидно, линеаризации ограничений (3.2) в точке xn: минимум ищется на касательной гиперплоскости W¢xn.

Один из распространенных методов решения задач с ограничениями, с которым мы еще столкнемся — так называемый метод штрафов. Он позволяет сводить задачу с ограничениями к задаче без ограничений и суть его заключается в наказании за невыполнение ограничений. Именно, вместо минимизации функции f0 с ограничениями (3.2) минимизируется функция fs(x) = f0(x) + s||f(x)||2 без ограничений, в которой s — положительный параметр.

Теперь рассмотрим постановку задач с ограничениями типа неравенств gj(x) £ 0, j = 1, ..., l (3.6).

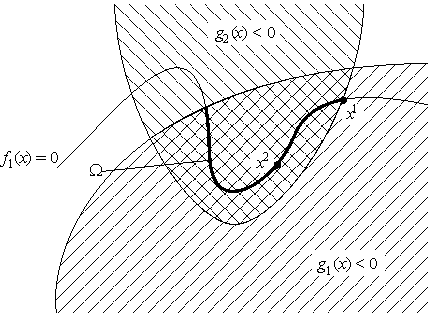
Рис. 3.2.

Определяются допустимые точки, локальный и глобальный, строгий и нестрогий минимумы. Так же мы будем использовать обозначения f и g для функций из Rm в Rk и Rl, соответственно, определяемые координатами fi и gj. Поэтому задачу (3.1)- (3.3), (3.6) можно записывать в виде

f(x) = Q, g(x) £ Q.

(напомним, что неравенство g(x) £ Q означает покоординатные неравенства).

f0(x) ® min, f(x) = Q, g(x) £ Q.

Через J(x) будет обозначаться множество индексов так называемых активных ограничений: J(x) = {j Î {1, ..., l}: gj(x) = 0} — это номера ограничений, которые в данной точке существенны.

Теорема (обобщенное правило множителей Лагранжа)

Пусть f0, f, g Î C1, а x* — локальное решение задачи f0(x) ® min, f(x) = Q, g(x) £ Q. Тогда найдутся такие l*0 Î R, l* Î Rk, m* Î Rl, не равные одновременно нулю, такие, что m*j ³ 0 при j Î J(x*) и

l*0 f ¢0(x*)+ l*i f ¢i(x*)+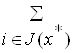m*j g¢j(x*) = Q. (3.7)

Регулярный случай

Так же, как и в случае ограничений-равенств, в случае общей задачи нелинейной оптимизации, необходимый признак, информативен только в случае, если l*0¹ 0. В этой ситуации можно разделить (3.7) на l*0 и, следовательно, считать его равным единице. Это позволяет ввести функцию Лагранжа L: Rm×Rk×Rk ® R (в регулярном случае) равенством

(x, l, m) = f0(x) + (l, f(x)) + (m, g(x)).

Условие регулярности в случае общей задачи выглядит сложнее. Именно, допустимая точка x называется регулярной, если векторы f ¢1(x),..., f ¢k(x) линейно независимы и для некоторого ненулевого вектора

hÎRm (f ¢i(x),h) = 0 при i = 1, ..., k и (g¢j(x),h) < 0 при j Î J(x).

Страницы: 1, 2, 3, 4, 5