Быстрый поиск

|

Если этот предел существует, то несобственный
интеграл называется сходящимся; если же предел не существует, - расходящимся.
Аналогично

и

Если функция f(x) имеет бесконечный
разрыв в точке с отрезка [a,b] и непрерывна при a <= x
< с и с < x < b, то по определению, полагают
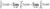
|
33.Числовые ряды.
Свойства сходящихся рядов.
Рассмотрим числовую
последовательность
(an)=a1,a2,...,an,…
Составим из нее новую
последовательность (Sn)
следующим образом:
S1=а1,
S2=a1+a2
S3=a1+a2+a3,,
Sn=a1+a2+…+аn=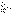
Sn+1=Sn+an+1
Выражение
a1+a2+…+аn+an+1+… (1)
обозначается символом 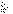 и
называется числовым рядом. и
называется числовым рядом.
Числа а1, а2,…,аn,… называются членами
ряда, а число аn- n – м членом или общим членом
ряда.
Простейшие свойства
числовых рядов
1о. Сходимость ряда не
нарушится, если произвольным образом изменить (переставить, добавить или
отбросить) конечное число членов ряда.
2о. Сходящийся ряд можно
почленно умножить на любой множитель  , т.е. если ряд , т.е. если ряд 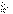 имеет сумму S, то ряд имеет сумму S, то ряд
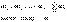
3о. Сходящиеся ряды можно
почленно складывать и вычитать, т.е. если даны ряды
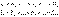
то ряд
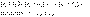
34.Необходимые условия
сходимости ряда.
Теорема: Пусть
числовой ряд
u1+u2+...+un+...
, (1)
сходится, а S - его сумма. Тогда при неограниченном возрастании
числа n членов ряда его общий член un стремится к нулю
Доказательство. Из условия теоремы имеем
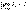 
Так как
Sn - Sn-1 = un
то
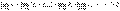
Следует отметить, что этот признак является лишь
необходимым, но не достаточным признаком сходимости ряда, так как можно
указать ряд, для которого выполняется равенство
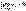 , ,
а он, однако не является сходящимся.
Так гармонический ряд
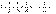 , ,
для которого
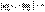 , ,
расходится.
Но согласно доказанному необходимому признаку сходимости ряда,
если
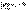 , ,
то ряд (1) расходится.
В самом деле, если бы он сходился, то
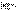
равнялся бы нулю.
Таким образом, доказанная нами теорема иногда позволяет, не
вычисляя суммы Sn, сделать заключение о расходимости того
или иного ряда. Например, ряд
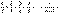 , ,
расходится, так как
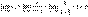 , ,
35.Сходимость
гармонического ряда.
-------(нету)
|
|
36.Необходимое и
достаточное условие сходимости ряда с неотрицательными членами.
Теорема 1. (Признак сравнения).
Пусть для членов рядов
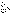 и и 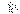
имеет место неравенство
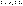 (8) (8)
n=1,2,…
Тогда:
1.
Если сходится ряд 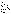 , то сходится и ряд , то сходится и ряд 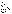
2.
Если расходится ряд 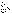 , то расходится и ряд , то расходится и ряд 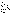 . .
Этот признак утверждает, что при выполнении
условия (8) из сходимости ряда с большими членами вытекает сходимость ряда с
меньшими членами, а из расходимости ряда с меньшими членами вытекает расходимость
ряда с большими членами.
Теорема 2. (Предельный признак сравнения).
Пусть члены рядов 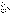 и и 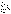 положительны и
положительны и
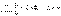
Тогда ряды 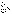 и и 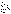 одновременно
сходятся или одновременно расходятся. одновременно
сходятся или одновременно расходятся.
37.Признак сравнения.
Пусть даны два ряда с
полжительными членами. 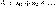 и и 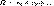 Причем, каждый член ряда Причем, каждый член ряда  не превосходит
соответствующего члена ряда не превосходит
соответствующего члена ряда  , то есть , то есть 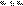 для всех для всех 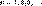 .
Тогда .
Тогда
·
если сходится ряд  с большими
членами, то сходится и ряд с большими
членами, то сходится и ряд  с меньшими членами; с меньшими членами;
·
если расходится ряд  с меньшими
членами, то расходится и ряд с меньшими
членами, то расходится и ряд  с большими членами. с большими членами.
Теорема остается верна, если
соотношения между членами рядов выполняются не для всех  , а лишь начиная с
некоторого номера , а лишь начиная с
некоторого номера 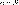 . .
При использовании признаков сравнений чаще
всего исследуемый ряд сравнивают с бесконечной геметрической пргрессией 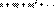 , которая
сходится при , которая
сходится при 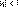 и расходится при и расходится при 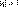 , или с
рядом , или с
рядом 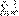 ,
который сходится при ,
который сходится при 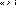 и расходится при и расходится при 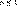 . .
38.Признак Даламбера.
Пусть l - предел отношения последующего члена un+1
ряда (1) к предидущему un при n®¥ , т.е.
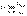
Тогда,
если l < 1, то ряд l сходится,
если l > 1, то ряд l расходится,
Если же l = 1, то вопрос о сходимости ряда (1) остается открытым.
Доказательство. Согласно определению предела
переменной величины, равенство
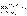
означает, что, начиная с некоторого номера n, выполняются
неравенства
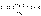
где e - наперед заданное сколь угодно малое
положительное число.
Рассмотрим три случая:
а) пусть l < 1 . Тогда всегда можно взять e настолько
малым, чтобы выполнялось неравенство
l + e < 1
и, начиная с некоторого n , неравенство
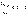
где q = l + e , в силу чего (см. теорему 1) ряд (1) будет сходящимся;
б) пусть l > 1 . Выбираем e так, чтобы
e = l - 1 > 0
Тогда l - e = 1 и
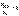
т.е. ряд (1) расходится (см. теорему 1)
в) пусть l = 1 . Тогда ряд (1) может быть как сходящимся,
так и расходящимся.
В самом деле, для гармонического ряда
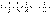
который расходится, имеем,
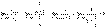
С другой стороны, ряд
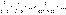
сходится, а для него также
|
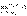
потому что
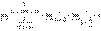
Таким образом, доказано, что если
то ряд (1)
сходится; если l > 1 , то ряд (1) расходится.
39.Интегральный признак
Коши.
Пусть  - непрерывная,
неотрицательная, монотонно убывающая функция, определенная при - непрерывная,
неотрицательная, монотонно убывающая функция, определенная при  . Тогда ряд . Тогда ряд 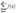 и интеграл и интеграл 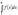 либо оба
сходятся, либо оба расходятся. либо оба
сходятся, либо оба расходятся.
Доказательство. Ввиду монотонности при всех  выполняются
неравенства выполняются
неравенства  .
Интегрируя, получаем .
Интегрируя, получаем 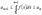 . Тогда . Тогда 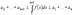 , или , или 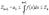 . Поэтому если . Поэтому если 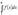 сходится, то сходится, то 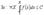 . Тогда . Тогда  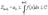 и и  , ,  ряд сходится. ряд сходится.
Пусть теперь наоборот,
известно, что ряд сходится. Тогда  . Взяв произвольное . Взяв произвольное  выберем выберем  так, чтобы так, чтобы  . Тогда . Тогда 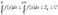 . Значит, . Значит, 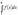 сходится. сходится.
40.Знакопеременные ряды.
Числовой
ряд, члены которого имеют различные знаки, называется знакопеременным рядом.
Пусть
дан знакопеременный ряд
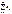 . (1) . (1)
Рассмотрим ряд, составленный
из модулей его членов:
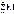 . (2) . (2)
Определение 1. Ряд (1)
называется условно сходящимся, если сам ряд (1) сходится, а ряд (2),
составленный из абсолютных величин, расходится.
Определение 2. Ряд (1) называется абсолютно сходящимся, если сам ряд (1) сходится и
ряд из абсолютных величин тоже сходится.
Теорема. Если ряд, составленный из абсолютных величин членов знакопеременного
ряда, сходится, то и сам ряд сходится (из абсолютной сходимости следует
условная).
41.Знакочередующиеся
ряды. Признак Лейбница.
Признак Лейбница.
Пусть дан знакочередующийся ряд
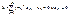 (монотонно стремится к 0), тогда А
сходится. (монотонно стремится к 0), тогда А
сходится.
Доказательство.
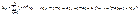
Т.к. 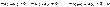
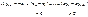 . .
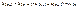 , , 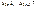 , то есть
последовательность частичных сумм , то есть
последовательность частичных сумм  убывает, а убывает, а  возрастает. возрастает.
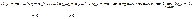 Каждая из последовательностей Каждая из последовательностей 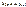 ограничена
и ограничена
и  . .
Следовательно, 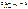 . .
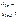 
Заметим, что:
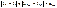 . .
42.Степенные ряды.
Признак Абеля.
Признак Абеля.
Пусть дан ряд:
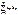 : : 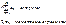 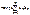
Доказательство.
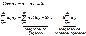 Доказано. Доказано.
43.Теорема об интервале
сходимости степенного ряда.
44.Теорема о радиусе
сходимости степенного ряда.
|
 Реферат: Шпора 2 по мат анализу
Реферат: Шпора 2 по мат анализу![]()
![]()
![]()
![]()


