Реферат: Методы решения некорректно поставленных задач

                               (A+aE)z º Az+az=u ,                                         (2:4,1)

где a>0 – числовой параметр. Решение уравнения

                                   za=(A+aE)-1u ,                                                  (2; 4,2)

при соответствующем выборе параметра a, принимается за приближенное решение уравнения (2; 0,1). Здесь Е — единичный оператор.

Замечание. Для оценки уклонения rF(zT,zd) приближенного решения от точного можно использовать мо­дуль непрерывности w обратного оператора на N.

Пусть u1, u2 Î N  и  rU(u1,u2)<= d. Тогда

            w(d,N)= sup  rF(A-1u1,A-1u2).

                                             u1,u2 ÎN

Очевидно, что если rU(uT,ud)<= d  и  zd=A-1ud , то

                                                         rF(zT,zd)<=w(d,N).

Вернемся к уравнению (2; 4,1). Если || Az ||<=d и w(d,DR) = sup || z ||,   то легко

                                                                                                                  DR

получить оценку уклонения  za от zT. Очевидно, что

                  || za - zT  ||<=||za1 - zT|| + ||za - za1||,                                      (2;4,3)

где

za1=(A + aE)-1uT.

Следовательно,

||za - zT||<=w(d,DR) + d/a.                              (2;4,4)

Если известен модуль непрерывности w(d,DR) или его мажоранта, то из (2; 4,4) можно найти значение пара­метра  w как функцию d, при котором правая часть в не­равенстве (2; 4,4) будет минимальной.

2. 5. Метод квазиобращения

2.5.1. Известно, что задача Коши для уравнения тепло­проводности с обратным течением времени является не­устойчивой к малым изменениям начальных значений. Неустойчивость сохраняется и в случаях, когда решение подчиняется некоторым дополнительным граничным усло­виям. Для устойчивого решения таких задач разработан метод квазиобращения . Мы изложим существо его для простейшего уравнения теплопроводности, не вда­ваясь в вопросы обоснования. Подробное изложение в применении к более широкому классу задач содержится в .

2.5.2. Рассмотрим прямую задачу. Пусть D — конечная область n-мерного евклидова пространства Rn точек x = (x1, x2, ..., xn), ограниченная кусочно-гладкой по­верхностью S, a t — время. Пусть, далее, j(x) — заданная непрерывная в D функция. Прямая задача состоит в на­хождении решения u=u(x,t) уравнения

                                                                   (2;5,1)

в области G º {x Î D, t > 0}, удовлетворяющего гранич­ным условиям

u(х, t) =0 при xÎS                                                     (2; 5,2)

и начальным условиям

u(x, 0)= j(x).                                                             (2; 5,3)

 Здесь

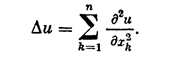
Известно, что решение такой задачи существует. Каждой функции j(x)ÎC  отвечает решение задачи (2; 5,1)— (2; 5,3). Будем обозначать его через u(х, t; j).

Обратная задача состоит в нахождении функции j(х) по известной функции u(х,t; j). В реальных задачах функция u(x,t;j) обычно получается в результате изме­рений и, следовательно, известна приближенно. Будем по­лагать, что uÎL2. Такая функция может и не соответст­вовать никакой «начальной» функции j(х). Таким обра­зом, может не существовать в классе функций С решения обратной задачи. Поэтому будем рассматривать задачу нахождения некоторого обобщенного решения обратной задачи.

Пусть заданы число T > 0 и функция y(x), опреде­ленная в области D, y(x) ÎL2. На функциях  j(х) класса С определен функционал

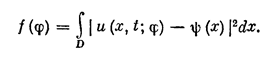
Обобщенным решением обратной задачи будем называть функцию j(х)., на которой достигается

                                                              f0=inf f(j)

        jÎC

Замечание. «Естественный» подход к решению этой задачи — выбрать функцию j(х).так, чтобы f(j)=0            .

Для этого достаточно найти решение прямой задачи

                    

u(x, t) = 0 для х Î S,  0 < t < T;

u(x,T) = y(x)

и положить j (x) = u(x,0). Но такая задача при задан­ной функции y(x) из L2, вообще говоря, неразрешима и, кроме того, неустойчива к малым изменениям функ­ции y(x).

На некотором классе обобщенных функций j (x) f0=0 . Поэтому рассматривается задача на­хождения приближенного значения f0 с заданным уровнем погрешности.

Для заданного числа e > 0 найти функцию je(x), на которой f (je)<=e.

Эта задача и решается методом квазиобращения.

Идея метода квазиобращения состоит в том, что вмес­то оператора теплопроводности   находится «близ­кий» ему оператор Вa , для которого задача с обращением отсчета времени

Baua = 0, x Î D, t < Т, a > 0;

ua (x,T)= y(x);

ua (x,t) = 0 для xÎ  S, t< Т

устойчива. Решив эту задачу, полагают j (x)=ua(x,0). Обычно в качестве оператора Вa берут оператор  и решают прямую задачу

xÎ D,          t<T,          a>0;

                                                        ua (x,T)= y(x);

                      ua (x,t) = 0 для xÎ  S,  0< t<= Т

                       Dua=0    для xÎ  S,  0< t<= Т.

Затем полагают

                                    j (x)=ua(x,0).

Следует отметить, что uaне сходится в обычном смыс­ле при a à0.

3.МЕТОД РЕГУЛЯРИЗАЦИИ РЕШЕНИЯ ОПЕРАТОРНЫХ УРАВНЕНИЙ

В главе предыдущем разделе рассмотрены случаи, когда класс возможных решений уравнения (2; 0,1) является компактом. Однако для ряда прикладных задач характерна ситуация, когда этот класс F не является компактом, и, кроме того, изме­нения правой части уравнения

                                                         Аz= u,                                               (3; 0,1)

связанные с ее приближенным характером, могут выво­дить за пределы множества AF — образа множества F при отображении его с помощью оператора А. Такие задачи  называются существенно некорректными. Был разработан новый подход к решению некорректно поставленных задач, позволяющий строить приближенные решения уравнения (3; 0,1), устойчивые к малым изме­нениям исходных данных, для существенно некорректных задач. В основе этого подхода лежит фундаментальное понятие регуляризирующего оператора (P.O.) . Для упрощения изложения в настоящей главе мы будем полагать, что в уравнении (3; 0,1) приближенной может быть лишь пра­вая часть и, а оператор А известен точно.

3.1. Понятие регуляризирующего оператора

3.1.1. Пусть оператор А в уравнении (3; 0,1) таков, что обратный ему оператор

A-1  не является непрерывным на множестве AF и множество возможных решений F не является компактом.

Пусть zT есть решение уравнения Az =uT, т. е. AzT=uT. Часто вместо uT мы имеем некоторый элемент ud и известное число d > 0 такие, что rU(ud,uT)<= d, т. е. вместо точных исходных данных (uT,А) мы имеем при­ближенные исходные данные (ud, А) и оценку их погрешности d. Задача состоит в том, чтобы по известным исход­ным данным (ud, A, d) найти приближение zd к элементу zt, обладающее свойством устойчивости к малым измене­ниям ud. Очевидно, что в качестве приближенного реше­ния zd уравнения (3; 0,1) нельзя брать точное решение этого уравнения с приближенной правой частью и= ud, т. е. элемент zT, определяемый по формуле

                                                         zd=A-1 ud

так как оно существует не для всякого элемента u ÎU и не обладает свойством устойчивости к малым изменениям правой части и.

Числовой параметр d характеризует погрешность пра­вой части уравнения (3;0,1). Поэтому представляется естественным определить zd с помощью оператора, зави­сящего от параметра, значения которого надо брать согла­сованными с погрешностью d исходных данных ud . Эта согласованность должна быть такой, чтобы при dà0, т. е. при приближении (в метрике пространства U) правой части ud уравнения (3; 0,1) к точному значению uT, при­ближенное решение zd стремилось бы (в метрике прост­ранства F) к искомому точному решению zt уравнения AzT =uT.

Пусть элементы zT Î F и  uT Î U связаны соотношением AzT = uT.

Определение 1. Оператор R(и, d), действующий из пространства U в пространство F, называется регуля-ризирующим для уравнения Az = и (относительно эле­мента uT), если он обладает свойствами:

1) существует такое число d1 > 0, что оператор R(u, d) определен для всякого d, 0<=d<=d1, и любого udÎU такого, что

                                      rU(ud,uT)<= d;

2) для всякого e > 0 существует d0=d0(e, ud)<=d1 такое, что из неравенства

                                    rU(ud,uT)<= d<=  d0;

следует неравенство

rF(zd,zT)<= e,

 где

zd=R(ud,d).

Здесь не предполагается, вообще говоря, однозначность оператора R(u,d). Через zd обозначается произвольный элемент из множества {R(ud,d)} значений оператора R(ud,d).

3.1.2. В ряде случаев целесообразнее пользоваться другим определением регуляризирующего оператора (P.O.).

Определение 2. Оператор R(u, a), зависящий от параметра a и действующий из U в F, называется регуляризирующим для  уравнения Az=и (относительно эле­мента uT), если он обладает свойствами:

1) существуют такие числа d1>0, a1>0, что опера­тор R(u, a ) определен для всякого a, принадлежащего промежутку (0, a1), и любого uÎU, для которого

rU(u,uT)<=d1;

2) существует такой функционал a=a(u, d), опреде­ленный на множестве   Ud1º{u; r(u,uT)<= d1} эле­ментов иÎU, что для любого e > 0 найдется число d(e)<=d1 такое, что если u1ÎU и rU(u1,uT)<= d<= d(e), то

rF(za,zT)<= e , где

za=R(u1, a(u1,d)).

В этом определении не предполагается однозначность оператора R(u1, a(u1,d)). Следует отметить, что при  a= d получаем определение 1 .

     3.1.3. Если rU(ud,uT)<= d, то известно, что в качест­ве приближенного решения уравнения (3; 0,1) с прибли­женно известной правой частью ud можно брать элемент za=R(d, a), полученный с помощью регуляризирующе­го оператора R(u, a ), где a=a(ud)=a1(d) согласовано с погрешностью исходных данных ud. Это решение назы­вается регуляризованным решением уравнения (3; 0,1). Числовой параметр  a называется параметром регуляриза­ции. Очевидно, что всякий регуляризирующий оператор вместе с выбором параметра регуляризации a, согласо­ванного с погрешностью исходных данных ud , a=a(ud), определяет устойчивый к малым изменениям правой час­ти и метод построения приближенных решений уравнения (3;0,1). Если известно, что rU(ud,uT)<= d, то согласно определению регуляризирующего оператора можно так выбрать значение параметра регуляризации a=a(ud) ,

что при dà0 регуляризованное решение R(ud,a(ud)) стремится (в метрике F) к искомому точному ре­шению zT, т. е. rF(zT,za(ud)). Это и оправдывает пред­ложение брать в качестве приближенного решения урав­нения (3; 0,1) регуляризованное решение.

Таким образом, задача нахождения приближенного решения уравнения (3; 0,1), устойчивого к малым изме­нениям правой части, сводится:

а) к нахождению регуляризирующих операторов;

б) к определению параметра регуляризации a по до­полнительной информации о задаче, например, по величи­не погрешности, с которой задается правая часть ud.

Описанный метод построения приближенных решений называется методом регуляризации.

3.2. О решении вырожденных и плохо обусловленных систем линейных алгебраических уравнений

3.2.1. Известно, с какими трудностями связано решение так называемых плохо обусловленных систем линей­ных алгебраических уравнений: малым изменениям пра­вых частей таких систем могут отвечать большие (выхо­дящие за допустимые пределы) изменения решения.

Рассмотрим систему уравнений

                                                            Аz=u,                                                              (3; 2,1)

где А — матрица с элементами aij, А ={aij}, z — иско­мый вектор с координатами zj , z={zj}, и — известный вектор с координатами иi ,u= {ui}, i, j =1, 2, ..., п. Система (3; 2,1) называется вырожденной, если опреде­литель системы равен нулю, detA = 0. В этом случае матрица А имеет равные нулю собственные значения. У плохо обусловленных систем такого вида матрица А имеет близкие к нулю собственные значения.

Если вычисления производятся с конечной точностью, то в ряде случаев не представляется возможным уста­новить, является ли заданная система уравнений вырож­денной или плохо обусловленной. Таким образом, плохо обусловленные и вырожденные системы могут быть не­различимыми в рамках заданной точности. Очевидно, такая ситуация имеет место в случаях, когда матрица А имеет достаточно близкие к нулю собственные значения.

В практических задачах часто правая часть и и эле­менты матрицы А, т. е. коэффициенты системы (3; 2,1), известны приближенно. В этих случаях вместо системы (3;2,1) мы имеем дело с некоторой другой системой Az=и такой, что ||A-A||<=h, ||u-u||<= d, где смысл норм обычно определяется характером задачи. Имея

вместо матрицы А матрицу A, мы тем более не можем высказать определенного суждения о вырожденности или невырожденности системы (3; 2,1).

В этих случаях о точной системе Аz=u, решение которой надо определить, нам известно лишь то, что для матрицы А и правой части и выполняются неравенства

||A-A||<=h, ||u-u||<= d. Но систем с такими исходными данными (А, и) бесконечно много, и в рамках извест­ного нам уровня погрешности они неразличимы. Поскольку вместо точной системы (3; 2,1) мы имеем приближенную систему Аz= и, то речь может идти лишь о нахождении приближенного решения. Но приближенная система Аz=и может быть неразрешимой. Возникает вопрос:

что надо понимать под приближенным решением систе­мы (3; 2,1) в описанной ситуации?

Среди «возможных точных систем» могут быть и вы­рожденные. Если они разрешимы, то имеют бесконечно много решений. О приближенном нахождении какого из них должна идти речь?

Таким образом, в большом числе случаев мы должны рассматривать целый класс неразличимых между собой (в рамках заданного уровня погрешности) систем урав­нений, среди которых могут быть и вырожденные, и неразрешимые. Методы построения приближенных реше­ний систем этого класса должны быть одними и теми же, общими. Эти решения должны быть устойчивыми к малым изменениям исходных данных (3; 2,1).

В основе построения таких методов лежит идея «от­бора». Отбор можно осуществлять с помощью специальных, заранее задаваемых функционалов W[ z ] , входящих в постановку задачи.

Неотрицательный функционал W[ z ] , определенный на всюду плотном в F подмножестве F1 множества F, называется стабилизирующим функционалом, если:

а) элемент zT принадлежит его области определения;

б) для всякого числа d>0 множество F1,d элементов z из F1 , для которых

Страницы: 1, 2, 3, 4