Реферат: Цифровая обработка сигналов

а. обратное Z-преобразование,

б. теорему  разложения,

в. теорему запаздывания к результатам деления полинома числителя на полином знаменателя.

Последний из перечисленных способов относится к численным методам решения поставленной задачи.

Пример. Определить импульсную характеристику цепи на рис.(2.6,б) по передаточной функции.

Решение.

Здесь H(Z) =.

Разделим числитель на знаменатель

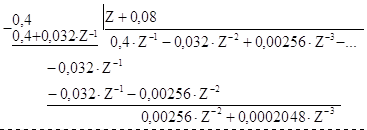
Применяя к результату деления теорему запаздывания, получаем

h(nT) = {0 ; 0,4 ; -0,032 ; 0.00256 ; ...}

Сравнивая результат с расчетами по разностному уравнению в предидущем примере, можно убедиться в достоверности расчетных процедур.

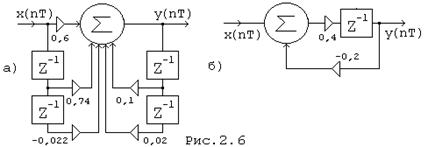
Предлагается определить самостоятельно импульсную реакцию цепи на рис.(2.6,а), применяя  последовательно оба рассмотренных метода.

В соответствии с определением передаточной функции, Z - изображение сигнала на выходе цепи можно определите как произведение Z - изображения сигнала на входе цепи и передаточной функции цепи:

Y(Z) = X(Z)ЧH(Z).            (2.11)

Отсюда, по теореме о свертке, свертка входного сигнала с импульсной характеристикой дает сигнал на выходе цепи

y(nT) =x(kT)Чh(nT - kT) =h(kT)Чx(nT - kT).   (2.12)

Определение выходного сигнала по формуле свертки находит применение не только в расчетных процедурах, но и в качестве алгоритма функционирования технических систем.

Пример.

 Определить сигнал на выходе цепи, схема которой приведена на рис.(2.6,б), если  x(nT) = {1,0;  0,5}.

Решение.

Здесь h(nT) = {0 ; 0,4 ; -0,032 ; 0,00256 ; ...}

Расчёт по (2.12)

n=0 : y(0T) = h(0T)x(0T) = 0;

n=1 : y(1T) = h(0T)x(1T) + h(1T) x(0T) = 0,4;

n=2 : y(2T)= h(0T)x(2T) + h(1T) x(1T) + h(2T) x(0T) = 0,168;

Таким образом   y(nT) = { 0;  0,4;  0,168; ... }.

В технических системах вместо линейной свертки (2.12) чаще применяется круговая или циклическая свертка .

2.6 Круговая свёртка .

Реальным сигналам соответствуют числовые последовательности конечной длины. Конечную числовую последовательность можно продолжить по оси времени путём периодического повторения и получить периодическую числовую последовательность. Периодической числовой последовательности соответствует спектр в виде периодической числовой последовательности. Обе последовательности имеют одинаковый период N и связаны формулами ДПФ.

Замена  реальных последовательностей периодическими позволяет повысить эффективность использования вычислительной техники применительно к дискретным  сигналам (скоростная свёртка, БПФ и др. )

Свёртка периодических последовательностей называется круговой и определяется на интервале равном одному периоду.

y(nT) =x(kT)Чh(nT - kT),   (2.13)

Линейная и круговая свёртки дают одинаковый результат, если соответствующим образом выбрать в круговой свёртке размер исходных последовательностей. Дело в том, что свёртка конечных последовательностей приводит к последовательности, размер которой N превышает длину каждой из исходных последовательностей и, по определению, равен

N = N1 + N2 - 1,      (2.14)

где N1 - длина последовательности x(nT),

N2 - длина последовательности h(nT).

Поэтому замена исходной последовательности на периодическую выполняется с таким расчётом, чтобы длина периода получилась равной N, добавляя с этой целью нули в качестве недостающих элементов.

Пример.

Вычислить круговую свёртку по данным примера в параграфе 2.4.

Решение.

Здесь, пренебрегая малыми значениями отсчётов представим импульсную реакцию в виде конечной числовой последовательности h(nT) ={0; 0,4 ; -0,032}.

Отсюда, поскольку  x(nT) = {1,0;  0,5},  с учётом  (2.14)

N1 = 2,N2 = 3,N = 4.

Следовательно исходные числовые последовательности запишутся так

x(nT) = {1,0;  0,5;  0;  0}, h(nT) ={0;  0,4; -0,032;  0}.

Отсюда, применяя (2.13), получаем

n=0:   y(0T) = x(0T)h(0T) + x(1T)h(-1T) + x(2T)h(-2T) + x(3T)h(-3T) = 0;

n=1:   y(1T) = x(0T)h(1T) + x(1T)h(0T)  + x(2T)h(-1T) + x(3T)h(-2T) = 0,4;

n=2:   y(0T) = x(0T)h(2T) + x(1T)h(1T)  + x(2T)h(0T)  + x(3T)h(-1T) = 0,168;

n=3:   y(0T) = x(0T)h(3T) + x(1T)h(2T)  + x(2T)h(1T)  + x(3T)h(0T) = -0,016;

Следовательно y(nT)= {0;  0,4;  0,168;  -0,016}, что совпадает с расчётами по линейной свёртке в примере параграфа 2.4.

Графики периодических числовых последовательностей x(nT), h(nT), y(nT) приведены на рис.(2.7).

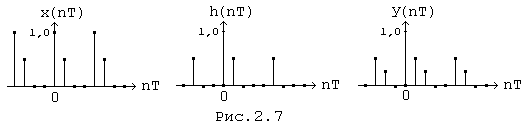
К периодическим числовым последовательностям, полученным изложенным выше способом, можно применить ДПФ, перемножить результаты и после выполнения обратного ДПФ получить последовательность y(nT), совпадающую с результатами расчётов по круговой свёртке.

2.7. Энергия дискретного сигнала.

Корреляция и энергетический спектр.

В качестве энергии дискретного сигнала принята мера

Wx =x2(nT),  (2.15)

соответственно в частотной области, согласно равенству Парсеваля,

Wx =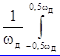X2(w)dw =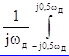X(jw)X*(jw)d(jw),  (2.16)

где X(jw) = X(w)ejj(w) - спектр сигнала x(nT),

X*(jw) = X(w)e-jj(w) - спектр x(-nT) в соответствии с теоремой о спектре инверсного сигнала,

X2(w) = X(jw)ЧX*(jw) = Sx(jw) - энергетический спектр сигнала x(nT).

На рис.(2.8) показан в качестве примера сигнал x(nT) и его инверсная копия x(-nT) для некоторого частного случая

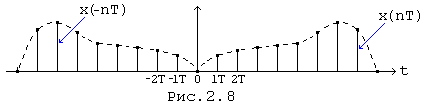
Энергетический спектр выражает среднюю мощность сигнала x(nT), приходящуюся на узкую полосу частот в окрестности переменной w.

Во временной области энергетическому спектру соответствует свертка инверных сигналов, что определяет корреляционную функцию Sx(nT) сигнала x(nT).

.   (2.17)

Согласно (2.17) и (2.15)  корреляционная функция в точке n = 0 равна энергии сигнала, т. е.

  (2.18)

Для периодических дискретных сигналов корреляционная функция и энергетический спектр связаны формулами  ДПФ

.  (2.19)

Отсюда получаются расчётные формулы энергии  периодических  дискретных последовательностей

,  (2.20)

что соответствует равенству Парсеваля для дискретных периодических сигналов. Корреляционная функция таких сигналов определяется по формуле круговой свёртки

.

Расчет энергии дискретного сигнала можно выполнить при необходимости, применяя равенство Парсеваля относительно Z - изображений сигнала и его инверсной копии (теорема энергий)

,  (2.21)

где  - Z - изображение корреляционной функции.

Умесно заметить, что применительно к случайным сигналам корреляционная функция чаще определяется формулой с весовым множителем , т.е.

,

соответственно для энергетического спектра

,

что приводит к результату, при котором среднее значение случайной величины  с ростом  N  сходится к постоянной величине.

Свертка сигнала с инверсной копией другого сигнала называется взаимной корреляцией этих сигналов.

2.8 Расчёт энергии сигнала в дискретной цепи.

В любой точке дискретной цепи энергию сигнала можно вычислить по известному сигналу или по корреляционной функции сигнала в этой точке. Корреляционную функцию сигнала в некоторой точке цепи можно определить не только по известному сигналу, но и по известной корреляционной функции входного сигнала и импульсной реакции

, (2.22)

где  - корреляционная функция сигнала на входе цепи,

 - корреляционная функция импулсного отклика в данной точке,

 - условный знак свёртки.

Докажем равенство (2.22).

.

В этом выражении в силу линейности цепи сигналы можно сочетать различными способами. Поэтому

,

что доказывает справедливость (2.22). Следовательно

.  (2.23)

Автокорреляционная функция является чётной функцией, поэтому применяя круговую свёртку (2.22), периоды  и  необходимо выровнять с таким расчетом, чтобы сохранить чётный характер этих функций.

Пример. Определить энергию сигнала на выходе цепи, если 

x(nT) = {0,5; 0,5}, h(nT) = {1,0; 0,5}.

Решение.

1. Расчет  во  временной  области.

Определяем сигнал на выходе цепи по формуле круговой свёртки

Отсюда .

2. Расчёт  в  частотной  области.

Вначале необходимо определить отсчёты спектра сигнала по формуле прямого ДПФ

.

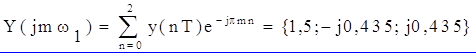Отсюда, согласно равенству Парсеваля,

.

3. Расчёт по формуле (2.23).

Определяем корреляционные функции  и .

Следовательно, .

увеличивая период  и  до N=5, получаем

,  .

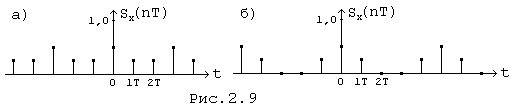
На рис.(2.9,а) показана периодическая последовательность  до увеличения периода, на рис. (2.9,б) - после увеличения периода .

Согласно (2.22)

.

Отсюда  .

В заключении рассмотрим  важный часный случай применения формулы (2.23).

Для случайных сигналов с нулевым средним

,  (2.24)

где  - дисперсия случайного сигнала x(nT).

Отсюда, учитывая (2.23),

.

Следовательно

,  (2.25)

Формула (2.25) применяется, в частности, для расчёта шумов квантования в цифровых цепях .

2.9 Секционирование.

Реальные сигналы могут иметь значительную протяжённость во времени, поэтому обработка таких сигналов на ЭВМ осуществляется посекционно. Расчёты по каждой секции  выполняются по формуле круговой свёртки

,

где h(nT) - импульсная характеристика, определяющая способ обработки сигнала .

Каждая секция  совмещается с предидущей секцией с учётом сдвига между секциями входного сигнала .

Применяются два основных метода секционирования: метод перекрытия с суммированием и метод перекрытия с накоплением.

1. Метод перекрытия с суммированием.

Сигнал x(nT) разбивается на секции длиной L. Отсюда- длина секции ,  - длина секции ,  - длина  .

Длина секции  больше длины секции  на . Поэтому смежные секции выходного сигнала  перекрываются  на интервале длиной . На интервале перекрытия необходимо выполнить арифметические операции по суммированию отсчётов.

2. Метод перекрытия с накоплением.

Сигнал x(nT)  разбивается на секции длиной L. Затем каждая секция наращивается слева участком предидущей секции длиной  . Поэтому

 - длина ,  - длина ,  - длина .

Искусственное удлинение каждой секции приводит к тому, что первые и последние  отсчётов секции  являются ложными и поэтому отбрасываются. Оставшиеся L отсчётов каждой секции, являются истинными, поэтому смежные секции  совмещаются без перекрытия и без зазора.

Пример. Осуществить посекционную обработку сигнала

x(nT) = { 1,0;  0,5 }, если h(nT)= { 1,0;  0,5 }.

Решение.

Применим метод перекрытия с накоплением.

Пусть L = 1. Отсюда ;

, поэтому после искусственного удлинения секций:

.

Выравниваем периоды сигналов для применения круговой свёртки:

N = N1 + N2- 1 = 3. Следовательно x0(nT)= {0;  0,4;  0}, x1(nT)= {0,4;  0,8;  0}, x2(nT)= {0,8; 0; 0} После свёртки по каждой секции и отбрасывания  отсчётов получаем:  отсюда

y(nT)= {0,4;  1,0;  0,4}.

Метод перекрытия с накоплением получил преимущественное распространение, поскольку здесь не требуется проведения дополнительных арифметичкских операций после обработки каждой секции.

3. Цифровые фильтры.

3.1 Цифровая система обработки сигналов.

Обработка дискретных сигналов осуществляется как правило в цифровой форме: каждому отсчёту ставится в соответствие двоичное кодовое слово и, в результате, действия над отсчётами заменяются на действия над кодовыми словами. Таким образом дискретная цепь становится цифровой цепью, цифровым фильтром (ЦФ). Перевод отсчётов в двоичные кодовые слова происходит в аналогово-цифровом преобразователе (АЦП). На выходе ЦФ (рис.3.1) осуществляется обратная операция:  кодовые слова в цифро-аналоговом преобразователе превращаются в отсчёты дискретного сигнала и, наконец, на выходе, синтезирующего фильтра (СФ) формируется обработанный аналоговый сигнал.

Страницы: 1, 2, 3, 4, 5, 6