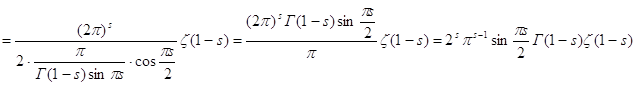Курсовая работа: Дзета-функция Римана
Курсовая работа: Дзета-функция Римана
Докажем тождественность ряда (1) и произведения (4).
Вспомнив формулу суммы геометрической прогрессии, получаем равенство 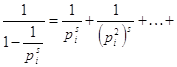
![]() Если
перемножить конечное число таких рядов, отвечающих всем простым числам, не
превосходящим заданного натурального числа N, то получившееся
частичное произведение окажется равным
Если
перемножить конечное число таких рядов, отвечающих всем простым числам, не
превосходящим заданного натурального числа N, то получившееся
частичное произведение окажется равным 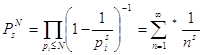 ,
где символ * означает, что суммирование распространяется не на
все натуральные числа, а лишь на те из них (не считая единицы), которые в своём
разложении содержат только простые числа меньшие N. Так как первые N натуральных
чисел этим свойством обладают, то
,
где символ * означает, что суммирование распространяется не на
все натуральные числа, а лишь на те из них (не считая единицы), которые в своём
разложении содержат только простые числа меньшие N. Так как первые N натуральных
чисел этим свойством обладают, то
![]() (5).
(5).
Сумма ![]() содержит
не все числа, большие N+1, поэтому, очевидно,
содержит
не все числа, большие N+1, поэтому, очевидно, ![]() .
Из (5) получаем
.
Из (5) получаем
![]() (6).
(6).
Ввиду сходимости ряда (1), выражение справа, представляющее
его остаток после N-го члена, стремится к нулю при N стремящимся к бесконечности, а ![]() есть
произведение (4). Значит из неравенства при
есть
произведение (4). Значит из неравенства при ![]()
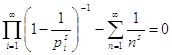 , что и требовалось доказать.
, что и требовалось доказать.
Формула
(4) важна потому, что она связывает натуральный ряд, представленный множеством
значений аргумента дзета-функции, со множеством простых чисел. Ещё один шаг в
этом направлении мы сделаем, оценив ![]() , а именно
показав, что
, а именно
показав, что ![]() , где
, где ![]() остаётся ограниченным при
остаётся ограниченным при ![]() .
.
Из
(4) следует, что 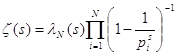 , где
, где ![]() N, а
N, а ![]() при
при ![]() . Возьмём логарифм от обеих
частей равенства, тогда
. Возьмём логарифм от обеих
частей равенства, тогда ![]()
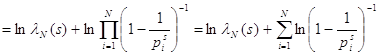 . Натуральные логарифмы под
знаком суммы разлагаются в ряд:
. Натуральные логарифмы под
знаком суммы разлагаются в ряд: 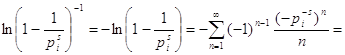
![]() . Подставив полученные
разложения в равенство и устремив N к бесконечности,
имеем
. Подставив полученные
разложения в равенство и устремив N к бесконечности,
имеем 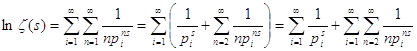 . Остаётся доказать
ограниченность последнего слагаемого. Ясно, что
. Остаётся доказать
ограниченность последнего слагаемого. Ясно, что ![]() .
Последнее равенство справедливо, так как
.
Последнее равенство справедливо, так как ![]()
![]() . Далее, очевидно,
. Далее, очевидно, ![]() , что и завершает
доказательство.
, что и завершает
доказательство.
На этом закончим изложение свойств дзета-функции Римана для действительного аргумента, так как наибольший теоретический и прикладной интерес представляет случай изложенный во второй главе.
Глава 2.
Все результаты первой главы, касающиеся дзета-функции Римана, были получены в предположении, что её аргумент s – действительное число. Однако, самые выдающиеся исследования и многочисленные важные приложения стали возможны лишь после включения в область определения функции комплексных чисел. Впервые рассмотрел дзета-функцию как функцию мнимого аргумента немецкий математик Бернгард Риман, глубоко изучивший её свойства и широко применявший её в теории чисел. В честь него функция получила своё название.
Для комплексной дзета-функции остаётся в силе определение,
данное в главе 1, с тем лишь изменением, что теперь там будет ![]() C. Возникает необходимость
найти новую область определения. С этой целью докажем следующее утверждение: в
полуплоскости
C. Возникает необходимость
найти новую область определения. С этой целью докажем следующее утверждение: в
полуплоскости ![]() (
(![]() действительная часть числа x) ряд
действительная часть числа x) ряд
![]() (1) сходится абсолютно.
(1) сходится абсолютно.
Пусть ![]() .
Подсчитаем абсолютные величины членов ряда (1),
.
Подсчитаем абсолютные величины членов ряда (1), ![]() .
Первый множитель содержит только вещественные числа и
.
Первый множитель содержит только вещественные числа и ![]() , так как
, так как ![]() . Ко второму же множителю
применим знаменитую формулу Эйлера, получим
. Ко второму же множителю
применим знаменитую формулу Эйлера, получим ![]()
![]() . Значит,
. Значит, ![]() . Ввиду сходимости ряда
. Ввиду сходимости ряда ![]() при α>1, имеем
абсолютную сходимость ряда (1).
при α>1, имеем
абсолютную сходимость ряда (1).
На своей области определения дзета-функция аналитична.
Действительно, при всяком q>0 и фиксированном α>1+q, числовой ряд ![]() мажорирует ряд из абсолютных величин
мажорирует ряд из абсолютных величин ![]() , где
, где ![]() , откуда, по теореме
Вейерштрасса, следует равномерная сходимость ряда в полуплоскости
, откуда, по теореме
Вейерштрасса, следует равномерная сходимость ряда в полуплоскости ![]() . Сумма же равномерно
сходящегося ряда из аналитических функций сама является аналитической функцией.
. Сумма же равномерно
сходящегося ряда из аналитических функций сама является аналитической функцией.
Нетрудно показать, что все полученные для дзета-функции формулы без изменений переносятся на случай комплексного аргумента. Доказательства претерпевают незначительные преобразования, связанные с переходом к абсолютным величинам.
В связи с этим замечанием становится возможным использовать
разложение дзета-функции в произведение 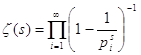 ,
где s теперь любое комплексное число, такое, что
,
где s теперь любое комплексное число, такое, что ![]() .
Применим его к доказательству отсутствия у функции
.
Применим его к доказательству отсутствия у функции ![]() корней.
корней.
Оценим величину ![]() ,
используя свойство модуля
,
используя свойство модуля ![]() :
: 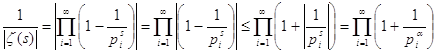 , где как обычно
, где как обычно ![]() . Так как
. Так как 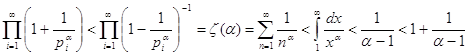 , то
, то ![]() , а
, а ![]() , следовательно,
дзета-функция в нуль не обращается.
, следовательно,
дзета-функция в нуль не обращается.
Вопрос о нулях дзета-функции, а также другие прикладные
вопросы получают новые широкие возможности для исследования, если
распространить её на всю комплексную плоскость. Поэтому, сейчас мы одним из многих
возможных способов найдём аналитическое продолжение дзета-функции и выведем её
функциональное уравнение, характеризующее и однозначно определяющее ![]() .
.
Для этого нам понадобится формула
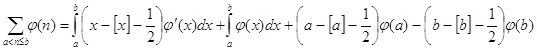 (2), которая выводится следующим образом. Используя свойства интегралов можно
записать
(2), которая выводится следующим образом. Используя свойства интегралов можно
записать 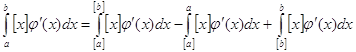 . Для любого d при
. Для любого d при ![]()
![]() , значит
, значит 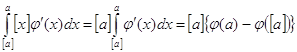 и
и 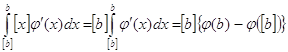 , а
, а 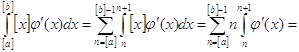 .
. 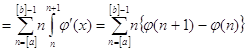 .
Следовательно,
.
Следовательно, 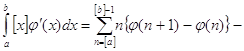
![]()
![]()
![]()
![]() . Интеграл
. Интеграл 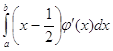 можно найти интегрированием
по частям, принимая
можно найти интегрированием
по частям, принимая ![]() ,
, ![]() ; тогда
; тогда ![]() , а
, а ![]() . В результате
. В результате 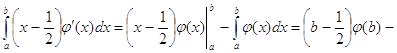
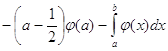 .
Вычтем из этого интеграла предыдущий и получим
.
Вычтем из этого интеграла предыдущий и получим 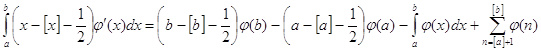 ,
отсюда легко следует равенство (2).
,
отсюда легко следует равенство (2).
Теперь положим в (2) ![]() ,
,
![]() , a и b – целые
положительные числа. Тогда
, a и b – целые
положительные числа. Тогда 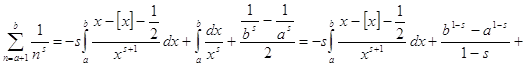
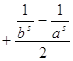 . Пусть сначала
. Пусть сначала ![]() , примем a=1, а b устремим к
бесконечности. Получим
, примем a=1, а b устремим к
бесконечности. Получим 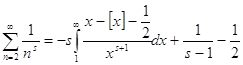 .
Прибавим по единице в обе части равенств:
.
Прибавим по единице в обе части равенств:
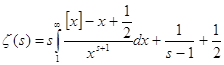 (3).
(3).
Выражение ![]() является
ограниченным, так как
является
ограниченным, так как ![]() , а функция
, а функция ![]() абсолютно интегрируема на
промежутке
абсолютно интегрируема на
промежутке ![]() при
при ![]() , то есть при
, то есть при ![]() ,
, ![]() .
Значит, интеграл
.
Значит, интеграл 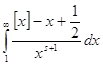 абсолютно сходится
при
абсолютно сходится
при ![]() , причём равномерно в любой
конечной области, лежащей в комплексной плоскости справа от прямой
, причём равномерно в любой
конечной области, лежащей в комплексной плоскости справа от прямой ![]() . Тем самым он определяет аналитическую
функцию переменной s, регулярную при
. Тем самым он определяет аналитическую
функцию переменной s, регулярную при ![]() . Поэтому
правая часть равенства (3) представляет собой аналитическое продолжение
дзета-функции на полуплоскость
. Поэтому
правая часть равенства (3) представляет собой аналитическое продолжение
дзета-функции на полуплоскость ![]() и имеет
там лишь один простой полюс в точке
и имеет
там лишь один простой полюс в точке ![]() с
вычетом, равным единице.
с
вычетом, равным единице.
Для ![]() можно
преобразовать выражение (3) дзета-функции. При
можно
преобразовать выражение (3) дзета-функции. При ![]() имеем
имеем
![]() , значит,
, значит, 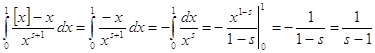 и
и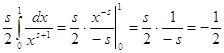 .
Теперь при
.
Теперь при ![]() (3) может быть записано в
виде
(3) может быть записано в
виде 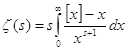 .
.
Немного более сложными рассуждениями можно установить,
что в действительности (3) даёт аналитическое продолжение дзета-функции на
полуплоскость ![]() . Положим
. Положим ![]() , а
, а ![]() , то есть
, то есть ![]() первообразная для
первообразная для ![]() .
. ![]() ограничена,
так как
ограничена,
так как 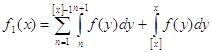 , а интеграл
, а интеграл 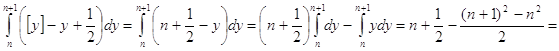
![]() и
и
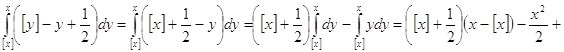
![]() ограничен
из-за того, что
ограничен
из-за того, что ![]() . Рассмотрим интеграл
. Рассмотрим интеграл
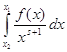 при x1>x2 и
при x1>x2 и ![]() . Проинтегрируем его по
частям, приняв
. Проинтегрируем его по
частям, приняв ![]() ,
, ![]() , тогда
, тогда ![]() , а по указанному выше
утверждению
, а по указанному выше
утверждению ![]() . Получаем
. Получаем 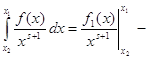
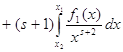 .
Возьмём
.
Возьмём ![]() , а
, а ![]() . Имеем
. Имеем ![]() ,
, ![]() ,
потому что
,
потому что ![]() является ограниченной
функцией. Значит,
является ограниченной
функцией. Значит,
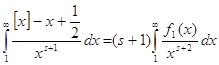 (4).
(4).
Пользуясь абсолютной сходимостью интеграла ![]() , если
, если ![]() , и ограниченностью функции
, и ограниченностью функции ![]() , делаем вывод, что в левой
части равенства (4) интеграл тоже сходится при
, делаем вывод, что в левой
части равенства (4) интеграл тоже сходится при ![]() .
Значит формулой (3) можно продолжить дзета-функцию и на полуплоскость правее
прямой
.
Значит формулой (3) можно продолжить дзета-функцию и на полуплоскость правее
прямой ![]() .
.
Нетрудно установить, что для отрицательных ![]()
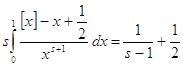 ,
поэтому из (3) имеем
,
поэтому из (3) имеем
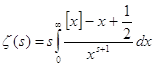 (5) при
(5) при ![]() .
.
Из теории рядов Фурье известно, что для нецелых значений x справедливо разложение в ряд
![]() (6).
(6).
Подставим его в равенство (5) и проинтегрируем ряд почленно:
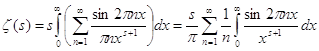 .
Сделаем в полученном интеграле подстановку
.
Сделаем в полученном интеграле подстановку ![]() ,
отсюда следует
,
отсюда следует ![]() , а
, а ![]() , и получим далее
, и получим далее 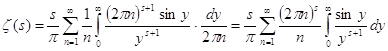 . Известно, что
. Известно, что 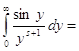
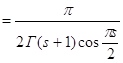 ,
значит
,
значит 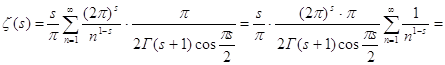
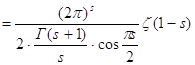 .
Из известного соотношения для гамма-функции
.
Из известного соотношения для гамма-функции ![]() ,
по формуле дополнения
,
по формуле дополнения ![]() ,
следовательно
,
следовательно ![]()