Реферат: Уравнения с параметрами

3)    при  а <0,5  уравнение  не  имеет  решений.

Проверка:

1)    при  подстановке  х = 0,5  в  уравнение  (7), равносильное  исходному, получим  неверное  равенство. Значит, х = 0,5  не  является  решением  (7)  и  уравнения  (6).

2)    при   подстановке  х1 = 0,5 ( 1 ± )  в  (7)  получим:

-0,5 ( 1 + ) =  – ( 0,5 ( 1 - ))2

      Так  как  левая  часть  равенства  отрицательна, то  х1  не  удовлетворяет  исходному  уравнению.

3)    Подставим  х2  в  уравнение (7):

                                           =

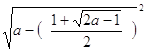Проведя  равносильные  преобразования, получим:

Если   , то  можно  возвести  полученное  равенство  в  квадрат:

                                

Имеем  истинное  равенство  при  условии, что

Это  условие  выполняется, если а ≥1. Так  как  равенство  истинно  при а ≥1, а  х2  может  быть  корнем  уравнения  (6)  при  а > 0,5, следовательно, х2 – корень  уравнения  при а ≥1.  

Тригонометрические  уравнения.

            Большинство  тригонометрических  уравнений  с  параметрами  сводится к  решению  простейших  тригонометрических  уравнений  трех  типов. При  решении  таких  уравнений  необходимо  учитывать  ограниченность  тригонометрических  функций            у = sin x   и  y = cos x. Рассмотрим  примеры.

Пример . Решить уравнение: cos =2а.

Решение: Так как Е(соs t)=[-1; 1], то имеем два случая.

1. При |a| > 0,5 уравнение не имеет решений.

2. При |a| ≤0,5  имеем:

а) =arccos2a+2πn. Так как уравнение имеет решение, если arccos2а+2πn≥0, то n может принимать значения n=0, 1, 2, 3,.... Решением уравнения является х = 1+(2πn+аrссоs2а)2

б) =-аrссоs2а+πn. Так как уравнение имеет решение при условии, что            -аrссоs2а+2πn>0, то n=1, 2, 3,..., и решение уравнения. х=1+(2πn-arccos2a)2 .

Ответ: если |a| > 0,5, решений нет;

если |a| ≤0,5  , х = 1+(2πn+аrссоs2а)2при n = 0, 1, 2,... и х=1+(2πn-arccos2a)2  при        n  N.

Пример . Решить уравнение:  tg ax2 =

Решение:.

      ах2 = +πn, n  Z

Если коэффициент при неизвестном зависит от параметра, то появляется особое значение параметра. В данном случае:

1. Если а=0, то уравнение не имеет решений.

2. Если а  0, то х2 = , n  Z

              Уравнение  имеет  решение, если  ≥0. Выясним, при  каких  значениях  n 

               и  а  выполняется  это  условие:

               ≥0

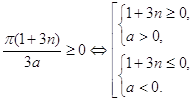
               откуда   n ≥    и  а > 0  или  n ≤   и  а < 0.

               Итак, уравнение  имеет  решение  х = ±  , если

                  1) а > 0    и  n = 1,2,3,…   или

                   2) а < 0   и  n  Z.

               Ответ: при  а = 0  решений  нет;

                           при  а > 0    и  n = 1,2,3,…   или  а < 0   и  n  Z  х = ±  .

Пример.  Решите  уравнение:  а sin bx = 1

Решение:  Особое  значение  параметра  а : а = 0.

1.    При  а = 0  решений  нет.

2.    При  а 0 sin bx = . Имеем  2  случая:

2.1. Если   > 1, то  решений  нет.

2.2. Если   ≤ 1, то  особое  значение  b = 0:

      2.2.1. Если  b = 0, то  решений  нет.

                                         2.2.2. Если  b 0, то  х =     

Ответ:   при  а = 0   или   > 1   и  а 0   или  а 0   b = 0    решений  нет;

              при  а 0   и   ≤ 1  и  b 0    х =     

Показательные    уравнения  с  параметрами.

            Многие  показательные  уравнения  с  параметрами  сводятся  к  элементарным  показательным  уравнениям  вида  а f (x)  = b φ(х)  (*), где  а > 0, b > 0.

            Область  допустимых  значений  такого уравнения находится  как  пересечение  областей  допустимых  значений  функций  f(x)  и  φ (х). Для  решения  уравнения  (*) нужно  рассмотреть  следующие  случаи:

1)    При  а = b = 1  решением  уравнения  (*)  является  область  его  допустимых  значений  D.

2)    При  а = 1, b ≠ 1  решением  уравнения  (*)  служит  решение  уравнения  φ(х) = 0  на  области  допустимых  значений  D.

3)    При  а ≠ 1, b = 1  решение  уравнения  (*)  находится  как  решение  уравнения      f(х) = 0  на  области  D.

4)    При  а = b  (а > 0, а ≠ 1, b >0, b ≠ 1)  уравнение  (*)  равносильно  уравнению        f(х) = φ(х)  на  области  D.

5)    При  а ≠ b  (а > 0, а ≠ 1, b >0, b ≠ 1)  уравнение  (*)  тождественно  уравнению

log c a f(x) =  log c b φ(x)  (c > 0, c ≠ 1)  на  области  D.

 

Пример. Решите  уравнение:  а х + 1 = b 3 – х

Решение. ОДЗ  уравнения:  х  R,  а > 0,  b >0.

       1)  При   а ≤ 0, b ≤ 0  уравнение  не  имеет  смысла.

       2)  При   а = b = 1,   х  R.

       3)  При  а = 1, b ≠ 1  имеем:  b 3 – х = 1  или  3 – х = 0  х = 3.

       4)  При  а ≠ 1, b = 1  получим:  а х + 1 = 1  или х + 1 = 0  х = -1.

       5)  При  а = b   (а > 0, а ≠ 1, b >0, b ≠ 1)  имеем: х + 1 =3 – х  х = 1.

       6)  При  а ≠ b  (а > 0, а ≠ 1, b >0, b ≠ 1)   прологарифмируем  исходное  уравнение

            по  основанию  а, получим:

           ,    х + 1 = ( 3 – х ) log a b ,

Ответ:  при   а ≤ 0, b ≤ 0  уравнение  не  имеет  смысла;

             при   а = b = 1,   х  R;

             при  а = 1, b ≠ 1  х = 3.

             при  а ≠ 1, b = 1  х = -1

             при  а = b   (а > 0, а ≠ 1, b >0, b ≠ 1)  х = 1

             при  а ≠ b  (а > 0, а ≠ 1, b >0, b ≠ 1)  

Логарифмические  уравнения  с  параметром.

            Решение  логарифмических  уравнений  с  параметрами  сводится  к  нахождению  корней  элементарного  логарифмического  уравнения. Важным  моментом  решения  уравнений  такого  типа  является   проверка  принадлежности  найденных  корней  ОДЗ  исходного  уравнения.

Пример. Решите  уравнение  2 – log (1 + х) = 3 log а  - log ( х 2 – 1 )2

Решение. ОДЗ: х > 1,  а > 0, а ≠ 1.

        Осуществим  на  ОДЗ  цепочку  равносильных  преобразований  исходного  уравнения:

log а а2 + log ( х2 - 1) =  log а ()3 + log a,

 

log а ( а2 (х2 - 1)) = log а (()3 ),

а2 (х2 - 1) = (х - 1) ,

а2 (х - 1) (х + 1) = (х - 1)

            Так  как  х ≠ -1  и  х ≠ 1, сократим  обе  части  уравнения  на  (х - 1)

а2 =

            Возведем  обе  части  полученного  уравнения  в  квадрат:

а4 (х + 1) =  х – 1  а4 х + а4 =  х – 1 х( 1 -  а4 ) =   а4 + 1

            Так  как  а ≠ -1  и  а ≠ 1, то 

            Для  того  чтобы  значения  х  являлось  решением  уравнения, должно  выполняться  условие  х > 1, то  есть 

            Выясним,  при  каких  значениях  параметра  а  это  неравенство  истинно:

,

            Так  как  а > 0, то  полученная  дробь  положительна, если  1 – а4 > 0, то  есть  при

а < 1.

            Итак, при  0 < a < 1,  x > 1, значит  при  0 < a < 1  х  является    корнем  исходного  уравнения.

Ответ:  при  а ≤ 0, а = 1  уравнение  не  имеет  смысла;

             при   а > 1  решений  нет;

             при  0 < a < 1 

ГЛАВА 2

§1. Разработка  факультативных  занятий  по  теме.

            В  общеобразовательных  классах  данная  тема  не    берется  в  явном  виде. Она  рассматривается  в  заданиях  более  сложного  характера. Например, при  изучении  темы  "Квадратные  уравнения", можно  встретить  следующие  задания:

1)    При  каком  р уравнение  х2 – 2х + 1 = р  имеет  один  корень ?

2)    При  каких  значениях  параметра  р сумма  корней  квадратного  уравнения

х2 + ( р 2 + 4р – 5 ) х – р = 0  равна  нулю ?

            В  классах  с  углубленным  изучением  математики уравнения  с  параметрами  целенаправленно  начинают  изучать  с  8  класса. Именно  в  этот  период  вводится  понятие  "параметр". Основная  задача – научить  учащихся  решать  уравнения  с  одним  параметром.

            Ученики  должны  уяснить, что  уравнения  с  параметром – это  семейство  уравнений, определяемых  параметром. Отсюда  и  вытекает  способ  решения:  в  зависимости  от  структуры  уравнения  выделяются  подмножества  множества  допустимых  значений  параметра  и для  каждого  такого  подмножества  находится  соответствующее  множество  корней  уравнения. Нужно  обратить  внимание  на  запись  ответа. В  нем  должно  быть  указано  для  каждого  значения  параметра (или  множества  его  значений), сколько  корней  имеет  это  уравнение  и  какого  вида.

            На  факультативных  занятиях  следует  разобрать  следующие  виды  задач:

1)    на  разрешимость: определить  параметры, при  которых  задача  имеет  хотя  бы  одно  решение  или  не  имеет  решений  вовсе.

2)    на  разрешимость  на  множестве: определить  все  параметры, при  которых  задача  имеет  m  решений  на  множестве  М  или  не  имеет  решений  на  множестве М.

3)    на  исследование: для  каждого  параметра  найти  все  решения  заданной  задачи.

Разработка  факультативных  занятий  приведена  в  приложении. Структура  следующая:

       Занятие№1. Решение  линейных  и  квадратных  уравнений 

                             с  параметрами.

Страницы: 1, 2, 3