Реферат: Пирамида
Реферат: Пирамида
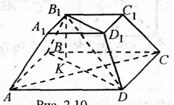
ABCD – основание пирамиды;
rSAB; rSBC; rSDC; rSDA – боковые грани пирамиды;
S – вершина пирамиды;
SA; SB; SC; SD – боковые рёбра пирамиды
SO – Высота пирамиды
Пирамида правильная – пирамида, у которой в основании лежит правильный многоугольник, а высота, опущенная из вершины пирамиды на плоскость основания, является отрезком, соединяющим вершину пирамиды с центром основания.
Свойства правильной пирамиды:
1. Всё боковые рёбра правильной пирамиды равны между собой.
2. Все боковые грани являются равными между собой равнобедренными треугольниками.
3. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на высоту боковой грани, которая называется апофемой.
![]()
![]() – периметр основания,
– периметр основания,
![]() - апофема.
- апофема.
Объем любой пирамиды равен одной трети произведения площади основания на высоту:
![]()
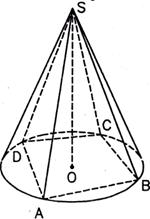
Пирамидой, вписанной в конус, является такая пирамида, основание которой есть многоугольник, вписанный в окружность основания конуса, а вершиной является вершина конуса. Боковые ребра такой пирамиды являются образующими конуса.
|
|
SABCD – пирамида, вписанная в конус.
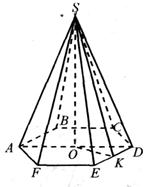
Пирамидой, описанной около конуса, является такая пирамида, основание которой есть многоугольник, описанный около основания конуса, а вершина совпадает с вершиной конуса. Плоскости боковых граней такой пирамиды являются касательными плоскостями конуса.
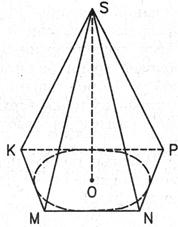
SKMNP – пирамида, описанная около конуса.
Пирамида усечённая - пирамида, которая получается следующим способом: берется произвольная пирамида, и через точку бокового ребра проводится плоскость, параллельная основанию пирамиды. Данная плоскость разделила пирамиду на две фигуры: подобную исходной пирамиду и многогранник, который называется усеченной пирамидой. Основаниями усеченной пирамиды служат подобные многоугольники.
Если усеченная пирамида получается из правильной пирамиды, то она называется правильной усеченной пирамидой. Боковые грани правильной усеченной пирамиды являются равными равнобедренными трапециями. Высота боковой грани называется апофемой правильной усеченной пирамиды. Перпендикуляр, опущенный из точки верхнего основания на нижнее, называется высотой усеченной пирамиды.
Площадь полной поверхности усеченной пирамиды равна сумме площадей оснований и боковых граней.

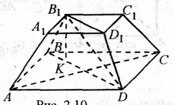
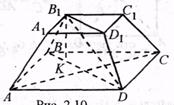
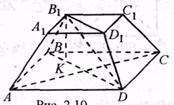
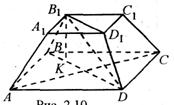
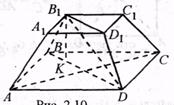
ABCDA1B1C1D1 – усечённая правильная пирамида,
O1O – высота,
B1E – апофема усечённой пирамиды.
Объём усечённой пирамиды вычисляется по формуле:
![]()
![]() – высота усеченной пирамиды,
– высота усеченной пирамиды,
![]() и
и![]() -
площади оснований усеченной пирамиды.
-
площади оснований усеченной пирамиды.
Площадь боковой поверхности правильной усеченной пирамиды вычисляется по формуле:
![]()
![]() и
и![]() -
периметры оснований усечённой правильной пирамиды,
-
периметры оснований усечённой правильной пирамиды,
![]() - апофема.
- апофема.
Теоремы.
- Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Доказательство:
Боковые
грани правильной пирамиды – равные равнобедренные треугольники, основания
которых – стороны основания пирамиды, а высоты равны апофеме. Площадь S боковой
поверхности пирамиды равна сумме произведений сторон основания на половину
апофемы d. Вынося множитель ![]() за скобки, получим в
скобках сумму сторон основания пирамиды, т.е. его периметр.
за скобки, получим в
скобках сумму сторон основания пирамиды, т.е. его периметр.
- Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
Задачи.
Задача №1
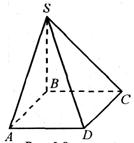
Построим линию пересечения плоскости грани МАВ пирамиды МАВCD с плоскостью грани MCD.
Решение: Плоскости МАВ и MCD имеют по условию общую точку М. Значит, по аксиоме (если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку) они пересекаются по прямой, проходящей через точку М. Найдем еще одну общую точку этих плоскостей. В соответствии с условием прямые АВ и CD лежат в одной плоскости. Построим точку их пересечения:
![]()
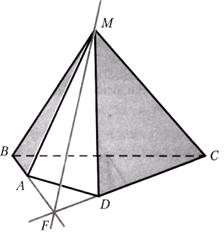
Точка F принадлежит прямой АВ, две точки которой лежат в плоскости МАВ. Тогда по аксиоме (Если две точки прямой принадлежат плоскости, то все точки прямой, определяемой ими, лежат в этой плоскости) и точка F лежат в плоскости МАВ.
Аналогично заключаем, что точка F лежит и в плоскости MCD. Таким образом, точка F — это вторая общая точка плоскостей МАВ и MCD. Итак, прямая MF — это искомая линия пересечения плоскостей МАВ и MCD.
Задача №2
На ребре МА пирамиды MABCD
взята точка Р, а в ее гранях MCD и МВС — соответственно точки Q и R. Построим
основной след секущей плоскости ![]() , проходящей через точки Р, Q и R.
, проходящей через точки Р, Q и R.
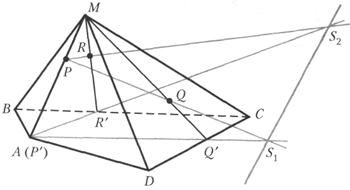
Решение: 1) Построим точки
Р', Q' и R' — проекции соответственно точек Р, Q и R на плоскость ABC из
центра М. Ясно, что точка Р' совпадает с точкой ![]() ,
,![]() .
.
Так как прямые МР и MQ пересекаются, то по
теореме (Через две пересекающиеся прямые проходит плоскость, и притом одна)
через них
проходит плоскость. По теореме этой плоскости принадлежат прямые PQ и P'Q'.
Построим точку ![]() .
.
Так как точка ![]() лежит на прямой PQ, две точки
которой принадлежат плоскости
лежит на прямой PQ, две точки
которой принадлежат плоскости![]() , то по аксиоме (Если две точки
прямой принадлежат плоскости, то все точки прямой, определяемой ими, лежат в
этой плоскости) точка
, то по аксиоме (Если две точки
прямой принадлежат плоскости, то все точки прямой, определяемой ими, лежат в
этой плоскости) точка ![]() принадлежит плоскости
принадлежит плоскости ![]() . Аналогично
заключаем, что точка
. Аналогично
заключаем, что точка ![]() принадлежит плоскости ABC. Итак,
плоскости
принадлежит плоскости ABC. Итак,
плоскости ![]() и
ABC имеют общую точку
и
ABC имеют общую точку ![]() . Тогда по аксиоме (если две
плоскости имеют общую точку, то они пересекаются по прямой, проходящей через
эту точку) эти плоскости пересекаются по прямой, проходящей через точку
. Тогда по аксиоме (если две
плоскости имеют общую точку, то они пересекаются по прямой, проходящей через
эту точку) эти плоскости пересекаются по прямой, проходящей через точку ![]()
Построим еще одну общую
точку плоскостей а и ABC. Например,
точку ![]() .Проведем
прямую
.Проведем
прямую ![]()
![]() Так как точки
Так как точки ![]()
![]() этой прямой лежат в
плоскости
этой прямой лежат в
плоскости ![]() ,
то по аксиоме (Если две точки прямой принадлежат плоскости, то все точки
прямой, определяемой ими, лежат в этой плоскости) прямая
,
то по аксиоме (Если две точки прямой принадлежат плоскости, то все точки
прямой, определяемой ими, лежат в этой плоскости) прямая ![]()
![]() лежит в плоскости
лежит в плоскости ![]() . Аналогично приходим к
выводу, что прямая
. Аналогично приходим к
выводу, что прямая ![]()
![]() лежит в плоскости ABC. Таким
образом, прямая
лежит в плоскости ABC. Таким
образом, прямая ![]()
![]() — это линия пересечения
плоскости а с плоскостью ABC, т.е. она является основным следом плоскости
— это линия пересечения
плоскости а с плоскостью ABC, т.е. она является основным следом плоскости ![]() .
.
Задача №3
Центр верхнего основания куба с
ребром, равным ![]() , соединен с
серединами сторон нижнего основания, которые также соединены в последовательном
порядке. Вычислить полную поверхность полученной пирамиды.
, соединен с
серединами сторон нижнего основания, которые также соединены в последовательном
порядке. Вычислить полную поверхность полученной пирамиды.
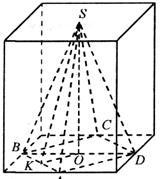
Решение: Так как ребро куба равно а, то сторона основания пирамиды
SABCD
равна ![]() Учитывая,
что ОК =
Учитывая,
что ОК = ![]() , найдём апофему пирамиды:
, найдём апофему пирамиды: ![]()
Значит,
![]() ,
, 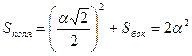
Ответ:
![]()
Задача №4
Апофема правильной
шестиугольной пирамиды равна h, а двугранный угол при основании равен ![]() . Найти полную поверхность
пирамиды.
. Найти полную поверхность
пирамиды.
|
|
Решение: Так
как ![]() , то
, то ![]() .
.
Основание
пирамиды – правильный шестиугольник, поэтому ![]() и
и
![]() . Тогда
. Тогда ![]() ,
т.е.
,
т.е. ![]() ,
,
![]() . Таким образом,
. Таким образом, ![]() ,
, ![]()
Окончательно
находим ![]()
Ответ: ![]()
Задача №5
В основании пирамиды лежит
квадрат. Две боковые грани перпендикулярны плоскости основания, а две другие
наклонены к нему под углом ![]() . Среднее
по величине боковое ребро равно
. Среднее
по величине боковое ребро равно ![]() . Найти
объём и полную поверхность пирамиды.
. Найти
объём и полную поверхность пирамиды.
|
|
Решение: По
условию, ![]() ,
, ![]() ,
, ![]() . Откуда
. Откуда ![]() .
.
Находим ![]() .
.
Полная поверхность
выразится так: ![]() , поскольку
, поскольку
![]() ,
, ![]() .
.
Но 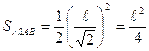 ,
, ![]()
Итак, ![]()
Ответ: ![]() ;
; ![]() .
.
Задача №6
Определить объём правильной четырёхугольной усечённой пирамиды, если её диагональ равна 18 см., а длины сторон оснований 14 и 10 см..
|
|
|
|
|
|
|
|
|
|
Решение:
Искомый объём выражается формулой ![]() , где
, где ![]()
![]() .
Найдём
.
Найдём ![]()
Имеем ![]() . Так как
. Так как ![]() - равнобедренная трапеция,
то
- равнобедренная трапеция,
то
![]() и
и ![]() т.е.
т.е.
![]() Итак,
Итак, ![]()
Ответ: ![]()
|
|
Используемые источники.
1. Весь Египет (Джованна Маджи, Паоло Джамбоне)
2. Математика. Справочник школьника (Г. Якушева)
3. Геометрия 10-11 класс (Л. С. Атасян, В. Ф. Бутузов)
4. Что такое. Кто такой. (А.Г. Алексин, С.П. Алексеев)
5. Геометрия (В.Н. Литвиненко)
6. http://www.devious.by.ru
7. Сборник задач по Математике (М.И. Сканави)