Реферат: Некоторые Теоремы Штурма

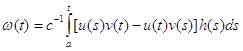;       (2.13)

(проще проверить это непосредственно). Общее решение уравнения (2.2) получается прибавлением к (2.13) общего решения   уравнения (2.1), что дает

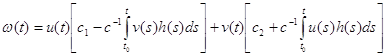.  (2.14)

Если замкнутый ограниченный интервал [a,b] содержится в J, то, полагая

,  , 

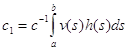мы получаем из (2.14) частное решение

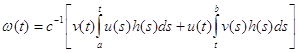.(2.15)

Оно может быть записано в виде

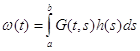,               (2.16)

где

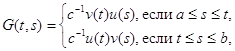        (2.17)

матрица С (t) зависит от , но не зависит от их про­изводных. В этом случае уравнение (2.1) и эквивалентная ему система (2.3) сводятся к системе

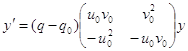.        (2.28)

 (xii) Если известно частное решение  уравнения (2.27), не равное нулю на J, то мы можем определить линейно независимые решения с помощью квадратур (см. (ix)) и затем найти матрицу, вхо­дящую в (2.28). В действительности, тот же результат можно полу­чить более прямым путем. Пусть уравнение (2.27) имеет решение  на интервале J. Заменим неизвестную функцию и в (2.1) на z, так что

.                       (2.29)

Функция z удовлетворяет дифференциальному уравнению

.

Умножая его на , мы получаем, что

  (2.30)

или, в силу (2.27), что

,                (2.31)

т. е. подстановка (2.29) приводит уравнение (2.1) к (2.30) или к (2.31). Мы могли также начинать не с решения  дифферен­циального уравнения (2.27), а с функции , имеющей непрерывную производную  и такой, что   непрерыв­но дифференцируема. При этом  определяется равенством (2.27), так что  . Подстановка (2.29) будет назы­ваться также вариацией постоянных.

(xiii) Подстановка Лиувилля. В качестве частного случая рас­смотрим (2.1) с р (t) = 1:

и" + q (t) и = 0.                       (2.32)

Предположим, что функция q (t) имеет непрерывную производную второго порядка, вещественна и не равна нулю, так что

±q (t) > 0, где ± = sgn  q (t)      (2.33)

не зависит от t. Рассмотрим вариацию постоянных

.           (2.34)

Тогда (2.32) сводится к (2.30), где , т. е. к уравнению

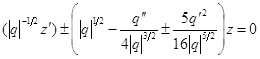     (2.35)

Замена независимых переменных , определенная соотношением

,                    (2.36)

переводит (2.35) в уравнение

   (2.37)

где

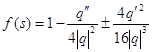   (2.38)

а аргументом функции q и ее производных служит функция t = t (s), обратная к функции s = s (f), определяемой из (2.36) с помощью квадратуры; см. (1.7). В этих формулах штрих означает дифферен­цирование по t, так что q' = dqldt.

Замена переменных (2.34), (2.36) называется подстановкой Лиувилля. Эта подстановка, или повторное применение ее, часто приводит к дифференциальному уравнению типа (2.37), в котором функция f (s) «близка» к постоянной. Простой предель­ный случай такой подстановки см. в упр. 1.1(с).

(xiv) Уравнения Риккати. В п. (xi), (xii) и (xiii) рассматривались преобразования уравнения (2.1) в различные линейные уравнения второго порядка или в соответствующие линейные системы двух уравнений первого порядка.  Иногда удобно преобразовать (2.1) в соответствующее нелинейное уравнение или систему. Для этого чаще всего используется следующий метод. Пусть

,    (2.39)

так что . Тогда после деления (2.1) на и результат можно записать в виде

.   (2.40)

Это уравнение называется уравнением Риккати, соответствующим (2.1). (В общем случае уравнение вида , где правая часть является квадратичным полиномом от г, называется дифференциальным уравнением Риккати.)

Читателю предоставляется проверка того факта, что если и (t) - решение уравнения (2.1), не равное нулю на t - интервале , то функция (2.39) является решением уравнения (2.40) на J'; обрат­но, если  - решение уравнения (2.40) на t-интервале , то, интегрируя (2.39), мы получаем решение

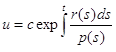              (2.41)

уравнения (2.1), не равное нулю ни в одной точке из J'.

 (xv) Преобразование Прюфера. В случае, когда уравнение (2.1) имеет вещественные коэффициенты, часто используется следующее преобразование . Пусть  -вещественное решение уравнения 2.1, и пусть

.

Поскольку и и и' не могут обратиться в нуль одновременно, то, фиксируя соответствующее значение функции  в некоторой точке , мы определяем с помощью второго из равенств (2.42) непре­рывно дифференцируемую функцию . Соотношения (2.42) пере­водят уравнение (2.1) в систему

 ,       (2.43)

            (2.44)

В уравнение (2.43) входит лишь одна из неизвестных функций . Если решение  уравнения (2.43) известно, то соответствую­щее решение уравнения (2.44) может быть найдено с помощью квадратуры.

Преимущество уравнения (2.43) по сравнению с (2.40) состоит в том, что всякое решение уравнения (2.43) существует на всем интервале J, где непрерывны р и q. Это видно из соотношения, свя­зывающего решения уравнений (2.1) и (2.43).

Упражнение 2.1. Проверьте, что если функция  непре­рывна на J и имеет локально ограниченную вариацию (т. е. имеет ограниченную вариацию на всех замкнутых ограниченных подин-тервалах из J) и если - вещественное решение уравнения (2.1), то равенства

  (2.45)

при фиксированном значении  для некоторого  однозначно определяют непрерывные функции , имеющие локально ограниченную вариацию и

Соотношения (2.46) и (2.47) следует понимать так, что интегралы Римана - Стильтьеса от обеих их частей равны. Обратно, (непре­рывные) решения системы уравнений (2.46), (2.47) определяют реше­ния уравнения (2.1) с помощью соотношений (2.45). Заметим, что если q (t) > 0, р (t) > 0 и функция q(t) р(t) имеет локально огра­ниченную вариацию, то, полагая , мы получаем q/, а соотношения (2.45), (2.46) и (2.47) переходят в равенства

  (2.48)

       (2.49)

.                  (2.50)

§ 3. Теоремы Штурма

В этом параграфе мы будем рассматривать только уравнение вида (2.1) с вещественными непрерывными коэффициентами р (t) > 0, q (t). Под «решением» мы будем понимать «вещественное, не­тривиальное (т. е. ) решение». Нас будет интересовать множество нулей решения u (t). Для изучения этих нулей часто оказывается полезным преобразование Прюфера (2.42), поскольку   тогда и только тогда, когда .

Лемма 3.1. Пусть  - вещественное решение уравне­ния (2.1) при , где  и  вещественны и непре­рывны. Пусть функция и (t) имеет в точности  нулей  при . Предположим, что  - непрерывная функция, определенная равенством (2.42), и  . Тогда и  при  .

Доказательство. Заметим, что в той точке t, где u=0, т. е. где , производная  в силу (2.43). Следовательно, функция  возрастает в окрестности точек, где  для некоторого целого j. Отсюда следует, что если  и , то  при , а также что если , то  при . Тем самым лемма дока­зана.

В теоремах этого параграфа будут рассматриваться два урав­нения

 

где функции  вещественны и непрерывны на интервале J. и

   .             (3.2)

В этом случае уравнение (3.1) называется мажорантой Штурма для (3.1) на J, а уравнение (3.1)-минорантой Штурма для (3.1). Если дополнительно известно, что соотношения

   (3.32)

или

 и    (3.31)

выполняются в некоторой точке , то уравнение (3.32) назы­вается строгой мажорантой Штурма для (3.31) на J.

Теорема 3.1 (первая теорема сравнения Штурма). Пусть коэффициенты уравнения  непрерывны на интервале J: , и пусть уравнение (3.32) является мажорантой Штурма для (3.11). Предположим, что функция  является решением уравнения (3.11) и имеет точно  нулей  при  ,а функция  удовлетворяет уравне­нию (3.12) и

   (3.4)

при . [Выражение в правой (соответственно левой) части нера­венства (3.4) при  полагается равным , если  (соответственно если ); в частности, соотношение (3.4) справедливо при , если .] Тогда  имеет при  пo крайней мере n нулей. Более того,  имеет по крайней мере n нулей при , если при  в (3.4) имеет место строгое неравенство или если уравнение (3.1 г) является стро­гой мажорантой Штурма для (3.11) при .

Доказательство. В силу (3.4) можно определить при  пару непрерывных функций  с помощью соотношений

   (3.5)

Тогда справедливы аналоги соотношения (2.43):

  (3.6j)

Поскольку непрерывные функции , гладким образом зависят от , решения системы (3.6) однозначно определяются своими начальными условиями. Из (3.2) следует, что  при  и всех . Поэтому последняя часть (3.5) и следствие III.4.2 означают, что

 для В частности, из  следует, что , и первая часть теоремы вытекает из леммы 3.1.

Чтобы доказать последнюю часть теоремы, предположим вна­чале, что при  в (3.4) имеет место строгое неравенство. Тогда . Обозначим через  решение уравнения (3.62), удовлетворяющее начальному условию , так что . Поскольку решение уравнения (3.62) однозначно определяется начальными условиями,  при . Неравенство, аналогичное (3.7), означает, что  потому .  Следовательно,  имеет n нулей при  .

Рассмотрим теперь тот случай, когда в (3.4) имеет место равен­ство, но в некоторой точке из  выполняется либо (3.31), либо (3.32). Запишем (3.62) в виде

,

где

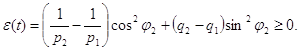
Если доказываемое утверждение неверно, то из уже рассмотрен­ного случая следует, что  при .Поэтому  и при . Так как  только в нулях функции , то отсюда следует, что  при  и .

Следовательно, если  при некотором t, то , т. е. .  Если (3.31) не выполняется ни при каком t из отрезка , то при некотором t имеет место (3.32), и потому (3.32) справедливо на неко­тором подинтервале из .  Но тогда на этом интервале   и потому . Однако это противоречит условию . Доказательство закончено.

Следствие 3.1 (теорема Штурма о разделении нулей). Пусть урав­нение (3.12) является мажорантой Штурма для (3.11) на интервале J, и пусть  - вещественные решения уравнений, (3.3j). Пусть  обращается в нуль в двух точках   интер­вала J. Тогда  имеет по крайней мере один нуль на . В частности, если  и вещественные линейно независимые решения уравнения  (3.11) (3.12). То нули функции  разделяют нули функции  и разделяются ими.

Заметим, что, последнее утверждение этой теоремы имеет смысл, поскольку нули функций  и  не имеют на J предельных точек. Кроме того, ,  не могут иметь общего нуля , так как в противном случае в силу того, что решения урав­нения (3.11) единственны, ,  где  (так что  и  не являются линейно независимыми).

Упражнение 3.1. (Другое доказательство теоремы Штурма о разделении нулей, когда p1(t)ºp2(t)>0, q2(t)³q1(t).)

Предположим, что u1(t)>0 при t1<t2<t3 и утверждение неверно: например, u2(t)>0 при t1£ t£t2. Умножая (p1(t)u¢)¢+q1(t)u=0, где u=u1, на u2, а (p2(t)u¢)¢+q2(t)u=0, где u=u2, на u1, вычитая и интегрируя по [t1,t2], получаем:

p(t)(u1¢u2-u1u2¢)³0, при t1£t£t2, где p=p1=p2. Это означает, что (u1/u2)¢³0; поэтому u1/u2>0 при t1<t£t2, т.е. получается, что u1(t2)>0 чего быть не может.

Решение:

(p1(t)u¢)¢+q1(t)u=0, u=u1

(p1(t)u1¢)¢+q1(t)u1=0.

Умножим левую часть равенства на u2, получим:

u2(p1(t)u1¢)¢+q1(t)u1u2=0.

Во втором уравнении проделаем соответствующие операции:

(p2(t)u¢)¢+q2(t)u=0, u2=u

(p2(t)u2¢)¢+q2(t)u2=0.

Умножим левую часть равенства на u1, получим:

u1(p2(t)u2¢)¢+q2(t)u1u2=0.

Вычитаем из первого уравнения второе, получим:

u2(p1u1¢)¢+q1u1u2-u1(p2u2¢)¢-q2u1u2=0, p=p1=p2

u2(pu1¢)¢+q1u1u2-u1(pu2¢)¢-q2u1u2=0

(u2(pu1¢)¢-u1(pu2¢)¢)+u1u2(q1-q2)=0

Упростим это уравнение,

u2(p¢u1¢+pu1¢¢)-u1(p¢u2¢+pu2¢¢)+u1u2(q1-q2)=0

Раскроем скобки, получим:

p¢u1¢u2+ pu1¢¢u2- p¢u1u2¢-pu1u2¢¢+u1u2(q1-q2)=0.

Сравнивая с формулой (2.2), получаем:

(p(u1¢u2-u1u2¢))¢+u1u2(q1-q2)=0

(p(u1¢u2-u1u2¢))¢-u1u2(q2-q1)=0

(p(u1¢u2-u1u2¢))¢=u1u2(q2-q1)=0.

Проинтегрируем это уравнение по [t1,t], получим:

[p(u1¢u2-u2¢u1)]¢dt = u1u2(q2-q1)dt,  где

u1u2>0, q2-q1³0.  Значит p(u1¢u2-u1u2¢)³0.

Т.о. (u1/u2)¢³0 Þ u1/u2>0.

Упражнение 3.2. с) Проверьте, что вещественные решения u(t) ¹0 уравнения u¢¢+m/t2u=0 (1/17) имеет не более одного нуля при t>0, если m£, и эти решения имеют бесконечно много нулей при t>0, если m>. В последнем случае множество нулей имеет две предельные точки t=0 и t=¥.

Решение: в §1 было рассмотрено упражнение 1.1 с), где показали, что функция u=tl является решением уравнения u¢¢+m/t2u=0 тогда и только тогда, когда l удовлетворяет уравнению  l(l-1)+ m=0. Решая его получили : l=±m.

Если m>1/4, то корни  l1 и  l2 – комплексные, т.е.

u=t1/2[cos (m-1/4 ln t)c1+c2sin(m-1/4 ln t)]

имеют бесчисленное множество нулей. В частности, если положить:

c1=sinu ,c2=cosu,

то получим:

u= t1/2[sin u cos (m-1/4 ln t)+cos u sin (m-1/4 ln t)]=

t1/2 [sin (u+m-1/4 ln t)].

Если m<1/4, то решение

u=с1t1/2+        +c2t1/2-

имеют не более одного нуля.

Так же, если m=1/4, то решение

u=c1t1/2+c2t1/2ln t

имеют не более одного нуля.

d) Рассмотрим уравнение Бесселя:

v¢¢+v¢/t+(1-m2/t2)v=0,                              (3.10)

где m-вещественный параметр. Вариация постоянных u=t1/2/v переводит уравнение (3.10) в уравнение:

u¢¢+(1-a/t2)u=0, где a=m2-1/4                  (3.11)

Проверим истинность этого утверждения u=t1/2v, следовательно:

v=u/t1/2=ut-1/2.

Найдём первую производную:

v¢=(ut-1/2) ¢=u¢t-1/2+u(t-1/2)¢=u¢t-1/2-1/2ut-3/2.

Теперь вторую производную:

v¢¢=(u¢t1/2) ¢-1/2(ut-3/2) ¢=u¢¢t-1/2 +u¢(t-1/2) ¢-1/2(u¢t-3/2+u(t-3/2) ¢)=

=u¢¢t-1/2 –1/2u¢t-3/2-1/2u¢t-3/2+3/4uut-5/2=

=u¢¢t-1/2-u¢t-3/2+3/4ut-5/2.

Подставляя в уравнение (3.10), получим:

v¢¢+v¢/t+(1-m2/t2)v=0.

u¢¢t-1/2-u¢t-3/2+3/4ut-5/2+1/t(u¢t-1/2-1/2ut-3/2)+(1-m2/t2)ut-1/2=0

t-1/2(u¢¢-u¢t-1+3/4ut-2+u¢t-1-1/2ut-2+u(1-m2/t2))=0

u¢¢+1/4ut-2+u(1-m2/t2)=0

u¢¢+u-m2u/t2+1/4ut-2=0

u¢¢+u-(m2u-1/4u)/t2=0

u¢¢+u-((m2-1/4)u)/t2=0

u¢¢+u-au/t2=0

u¢¢+(1-a/t2)u=0, где a=m2-1/4.

Покажем, что нули вещественного решения v(t) уравнения (3.10) образуют при t>0 такую последовательность t1<t2<…, что tn-tn-1®p при n®¥.

Так как в уравнении

u¢¢+(1-a/t2)u=0, т.е. уравнение

u¢¢+(1-(m2-1/4)/t2)u=0

m - постоянное число, то при m³1/4 и при t – достаточно большое, то выражение

1-(m2-1/4)/t2®1, т.е. если уравнение

u¢¢+(1-(m2-1/4)/t2)u=0

сравнить с уравнением u¢¢+u=0, то расстояние между последовательными нулями стремится к p, т.е. tn-tn-1®p при n®¥.

Теорема 3.2 (вторая теорема сравнения Штурма). Пусть выпол­нены условия первой части теоремы 3.1 и функция  имеет точно n нулей при . Тогда соотношение (3.4) выполняется при  [где выражение в правой (соответственно левой) части (3.4) при  полагается равным , если (соответственно,)]. Кроме того, при  в (3.4) имеет место строгое неравенство, если выполнены условия последней части теоремы 3.1.

Доказательство этого утверждения содержится по существу в доказательстве теоремы 3.1, если заметить, что из предположения о числе нулей функции  вытекает последнее неравенство в сле­дующей цепочке: . Аналогично, в предположениях последней части теоремы доказательство тео­ремы 3.1 дает неравенство .

Использованная литература:

1. Ф. Хартман. Обыкновенные дифференциальные уравнения: Учебн. пособие./ Пер. с англ. И.Х.Сабитова, Ю.В.Егорова; под ред. В.М.Алексеева.-М.: изд.”Мир”, 1970г.-720 с.

2. В.В.Степанов. Курс дифференциальных уравнений. Гос.изд. “Технико-теор. литер.”-М., 1953г.-468 с.

3. Большая Советская Энциклопедия. /Под ред. А.М.Прохорова. Изд. 3-е., М., “Советская Энциклопедия”, 1978г., т.29. “Чачан-Эне-ле-Бен.” – 640 с.

4. Г.Вилейтнер. “История математики от Декарта до середины 19-го столетия.” М., изд. “Наука.”, 1966г. – 508 с.

5. История математики с древнейших времён до начала 19-го столетия. /Под ред. Юшкевича А.П., т.3 /Математика 18-го столетия/., изд. “Наука.”, М., 1972г. – 496 с.