Учебное пособие: Анализ временных рядов

– дисперсия

;

– стандартное отклонение

– автокорреляционная функция

 

– частная автокорреляционная функция

Заметим, что в операторе функции  усреднение происходит при неизменном t , то есть имеется математическое ожидание по множеству реализаций (вообще-то говоря, потенциальных поскольку «в реку времени нельзя войти дважды»).

Рассмотрим введенные числовые характеристики для стационарных процессов. Из определения стационарности следует, что для любых s, t и  

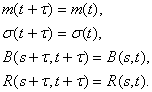
положив  = - t, получаем

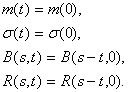 (1)

Выходит, у стационарного процесса математическое ожидание и дисперсия одинаковы при любом t, а автоковариационная и автокорреляционная функции зависят не от момента времени s или t, а лишь от их разности (лага).

Отметим, что выполнение свойств (1) еще не влечет стационарности в смысле определения из п.6. Тем не менее постоянство первых двух моментов, а также зависимость автокорреляционной функции только от лага определенно отражает некоторую неизменность процесса во времени. Если выполнены условия (1), то говорят о стационарности процесса в широком смысле, тогда как выполнение условий ( ) означает стационарность в узком (строгом) смысле.

Данное выше определение белого шума надо трактовать в узком смысле. На практике часто ограничиваются белым шумом в широком смысле, под которым понимают временной ряд (случайный процесс), у которого =0 и

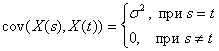
Отметим, что гаусовский процесс, стационарный в узком смысле, стационарен и в широком смысле.

О стационарности в широком смысле судить гораздо проще. Для этого используют различные статистические критерии, базирующиеся на одной реализации случайного процесса.

8.Оценивание числовых характеристик временного ряда

Оценивание числовых характеристик случайного временного ряда в каждый момент времени требует набора реализаций (траекторий) соответствующего случайного процесса. Хотя время и не воспроизводимо, однако условия протекания процесса иногда можно считать повторяющимися. Особенно это характерно для технических приложений, например, колебания напряжения в электрической сети в течении суток. Временные ряды, наблюдаемые в разные сутки, можно считать независимыми реализациями одного случайного процесса.

Иная ситуация при исследовании процессов социально-экономической природы. Как правило, здесь доступна единственная реализация процесса, повторить которую не представляется возможным. Следовательно, получить оценки среднего, дисперсии, ковариации нельзя. Однако для стационарных процессов подобные оценки все-таки возможны. Пусть  наблюденные значения временного ряда в моменты  соответственно. Традиционная оценка среднего  может служить оценкой математического ожидания стационарного (в широком смысле) случайного процесса.

Ясно, что такая оценка для стационарного ряда будет несмещенной. Состоятельность этой оценки устанавливается теоремой Слуцкого, которая в качестве необходимого и достаточного условия требует чтобы

,

где  – автокорреляционная функция процесса.

Точность оценивания среднего зависит от длины N ряда. Считается, что длина N всегда должна быть не меньше так называемого времени корреляции, под которым понимают величину

T =.

Величина Т дает представление о порядке величины промежутка времени , на котором сохраняется заметная корреляция между двумя значениями ряда.

Рассмотрим теперь получение оценок значений автокорреляционной функции. Как и прежде,  – наблюденные значения временного ряда. Образуем (N-1) пар . Эти пары можно рассматривать как выборку двух случайных величин, для которых можно определить оценку стандартного коэффициента корреляции . Затем составим (N-2) пар  и определим оценку  и т.д. Поскольку при подсчете очередного  объем выборки меняется, меняется значение среднего и стандартного отклонения для соответствующего набора значений. Для упрощения принято измерять все переменные относительно среднего значения всего ряда  и заменять дисперсионные члены в знаменателе на дисперсию ряда в целом, то есть

,

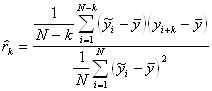где - среднее, равное .

При больших N расхождение в оценках незначительные. На практике k берут не выше N/4.

Если ряд рассматривается как генеральная совокупность бесконечной длины, то говорят об автокорреляциях (теоретических) и обозначают их . Массив коэффициентов  или соответствующих им выборочных коэффициентов  содержат весьма ценную информацию о внутренней структуре ряда. Совокупность коэффициентов корреляции, нанесенная на график с координатами k (лаг) по оси абсцисс и  либо  по оси ординат, называют коррелограммой (теоретической или выборочной соответственно).

Точностные характеристики оценки  получены для гауссовских процессов. В частности, для гаусовского белого шума, у которого все корреляции равны нулю, . Математическое ожидание  для гауссовского белого шума оказывается не равным нулю, а именно, , то есть оценка  оказывается смещенной. Величина смещения убывает с ростом объема выборки и не столь существенна в прикладном анализе.

Оценка  асимптотически нормальна при , что дает основание для построения приблизительного доверительного интервала. Широко применяемый 95%-интервал есть .

Границы доверительного интервала, нанесенные на график, называют доверительной трубкой. Если коррелограмма некоторого случайного процесса не выходит за пределы доверительной трубки, то этот процесс близок к белому шуму. Правда, это условие можно считать лишь достаточным. Нередко выборочная коррелограмма гауссовского белого шума содержит один, а то и два выброса среди первых 20 оценок , что естественно затрудняет интерпретацию подобной коррелограммы.

Наряду с автокорреляционной функцией при анализе структуры случайного временного ряда используется частная автокорреляционная функция, значения которой суть частные коэффициенты корреляции.

9. Свободные от закона распределения критерии проверки ряда на случайность

Простейшей гипотезой, которую можно выдвинуть относительно колеблющегося ряда, не имеющего явно выраженного тренда, является предположение, что колебания случайны. В случайных рядах, согласно гипотезе, наблюдения независимы и могут следовать в любом порядке. Для проверки на случайность желательно использовать критерий, не требующий каких-либо ограничений на вид распределения совокупности, из которой, по предположению, извлекаются наблюдаемые значения.

1.   Критерий поворотных точек состоит в подсчёте пиков (величин, которые больше двух соседних) и впадин (величин, которые меньше двух соседних). Рассмотрим ряд y1,...,yN.

пик впадина

 yt-1 < yt > yt+1 yt-1 > yt < yt+1

yt-1 yt yt+1 yt-1 yt yt+1

Рис. Поворотные точки.

Для определения поворотной точки требуются три последовательных значения. Начальное и конечное значения не могут быть поворотными точками, т. к. неизвестно y0 и yN+1. Если ряд случаен, то эти три значения могут следовать в любом из шести возможных порядков с равной вероятностью. Только в четырёх из них будет поворотная точка, а именно, когда наибольшее или наименьшее из трёх значений находится в середине. Следовательно, вероятность обнаружения поворотной точки в любой группе из трёх значений равна 2/3.

 с с c c c c

 b b b b b b

 а а a a a a

Рис. Варианты взаимного расположения трёх точек.

Для группы из N величин определим счётную переменную Х.

ì 1, если yt-1 < yt > yt+1 или yt-1 > yt < yt+1

Х = í

î 0, в противном случае.

Тогда число поворотных точек р в ряде есть просто , а их математическое ожидание есть М[p]=2/3(N-2). Дисперсия числа поворотных точек вычисляется по формуле D[p]=(16N-29)/90, а само распределение близко к нормальному.

2.   Критерий, основанный на определении длины фазы

Интервал между двумя поворотными точками называется фазой. Для того , чтобы установить наличие фазы длины d (например, восходящей) , нужно обнаружить d+3 членов, содержащих падение от первого члена ко второму ,затем последовательный подъем до (d+2)-го члена и падение к (d+3)-ему члену.

 

 

1 2 3 4 d+1 d+2 d+3 N

рис. 3. Фаза длины d.

Рассмотрим группу из d+3 чисел, расположенных в порядке возрастания. Если, не трогая двух крайних членов, извлечь пару чисел из оставшихся d+1 и одно из них поставить в начало, а другое в конец, получим фазу длины d. Существует  способов такого выбора пары чисел и каждый член пары может быть поставлен в любой конец, следовательно число восходящих фаз равно d(d+1).

Кроме того, поворотные точки будут иметь место, если первый член последовательности поставить в конец, а любой из оставшихся, за исключением второго, поместить в начало. Число таких последовательностей составит (d+1) . Еще столько же последовательностей получиться если последний член в исходной, возрастающей, последовательности поставить в начало, а любой другой, кроме последнего, в конец. Во избежании двойного счета следует исключить случай, когда первый член ставится на последнее место, а последний на первое. Таким образом, в последовательности из (d+3) чисел с фазой длиной d число случаев роста составит

Страницы: 1, 2, 3, 4, 5, 6