Быстрый поиск

Учебное пособие: Анализ временных рядов

(Здесь для удобства представления знаки ~ и Ù опущены).

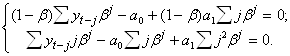
С учетом того что

, ,

получаем

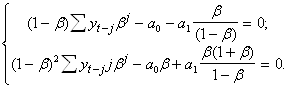
Запишем : .

Эту операцию можно рассматривать как сглаживание 1-го порядка. По аналогии построим сглаживание 2-го порядка:

; .

;

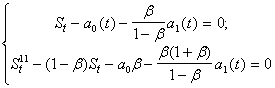
Рассмотренную выше процедуру можно обобщить на случай полиномиальных трендов более высокого порядка n , при этом алгебраические выражения будут сложнее. Например, если модель описывается параболой, то используется метод тройного экспоненциального сглаживания.

5. Оценивание и исключение сезонной компоненты

Сезонные компоненты могут представлять самостоятельный интерес либо выступать в роли мешающего фактора. В первом случае необходимо уметь выделять их из ряда и оценивать параметры соответствующей модели. Что же касается удаления сезонной компоненты из ряда, то здесь возможны несколько способов.

Рассмотрим сначала процедуру оценивания сезонных эффектов. Пусть исходный ряд является полностью аддитивным, то есть

Необходимо оценить по наблюденным . Иными словами, необходимо получить оценки коэффициентов индикаторной модели.

Как уже отмечалось, сезонный эффект проявляется на фоне тренда, поэтому вначале необходимо оценить трендовую составляющую одним из рассмотренных методов. Затем для каждого сезона вычисляют все относящиеся к нему разности

где, как обычно, - наблюденное значение ряда, - оцененное значение тренда.

Каждая из этих разностей дает совместную оценку сезонного эффекта и случайного компонента, отличного, правда, от исходного в силу взятия разностей.

Производя усреднение полученных разностей, получают оценки эффектов. Полагая, что исходный ряд содержит целое число k периодов сезонности и ограничиваясь простым средним, имеем

С учетом условия репараметризации, требующим, чтобы сумма сезонных эффектов равнялась нулю, получаем скорректированные оценки

В случае мультипликативного сезонного эффекта, когда модель ряда имеет вид

вычисляют уже не разности, а отношения

В качестве оценки сезонного индекса выступает среднее

На практике считается, что для оценки сезонных эффектов временной ряд должен содержать не менее пяти-шести периодов сезонности.

Перейдем теперь к способам удаления сезонного эффекта из ряда. Таких способов два. Первый из них назовем «послетрендовый». Он является логическим следствием рассмотренной выше процедуры оценивания. Для аддитивной модели удаление сезонной компоненты сводится к вычитанию оцененной сезонной компоненты из исходного ряда. Для мультипликативной модели значения ряда делят на соответствующие сезонные индексы.

Второй способ не требует предварительной оценки ни трендовой, ни сезонной компонент, а основывается на использовании разностных операторов.

Разностные операторы.

При исследовании временных рядов часто имеется возможность представить детерминированные функции времени простыми рекуррентными уравнениями. К примеру, линейный тренд

(1)

можно записать как

(2)

Последнее соотношение получается из (1) сравнением двух значений ряда для соседних моментов t-1 и t . Учитывая, что соотношение (2) справедливо и для моментов t-2 и t-1, так что , модель (1) можно записать и в виде

(3)

Модель (3) не содержит явно параметров, описывающих тренд. Более компактно описанные преобразования можно описать, используя операторы взятия разности назад

Модели (2) и (3) можно записать как

, .

Выходит, разность второго порядка полностью исключает из исходного ряда линейный тренд. Легко видеть, что разность порядка d исключает из ряда полиномиальный тренд порядка d-1. Пусть теперь ряд содержит сезонный эффект с периодом t, так что

(4).

Процедура перехода от ряда (t = 1,2,...,T) к ряду называется взятием первой сезонной разности, а оператор сезонным разностным оператором с периодом t. Из (4) следует, что

Выходит, взятие сезонной разности исключает из временного ряда любую детерминированную сезонную компоненту.

Иногда оказываются полезными сезонные операторы более высоких порядков. Так, сезонный оператор второго порядка с периодом t есть

Если ряд содержит и тренд, и сезонную составляющую, их можно исключить, последовательно применяя операторы и .

Легко показать, что порядок применения этих операторов не существенен:

Отметим также, что детерминированный тренд, состоящий из тренда и сезонной компоненты, после применения операторов и полностью вырождается, то есть . Однако записав последнее уравнение в рекуррентной форме, получаем

Из последнее соотношения видно, каким образом ряд можно неограниченно продолжать, имея вначале по крайней мере t+1 последовательных значения.

6. Модели случайной составляющей временного ряда

линейный ряд временной система

Для удобства изложения условимся обозначать здесь случайные величины так, как это принято в математической статистике – строчными буквами.

Случайным процессом X(t) на множестве Т называют функцию, значения которой случайны при каждом t Î T. Если элементы Т счетные (дискретное время), то случайный процесс часто называют случайной последовательностью.

Полное математическое описание случайного процесса предполагает задание системы функций распределения:

– для каждого t Î T , (1)

– для каждой пары элементов

(2)

и вообще для любого конечного числа элементов

(3).

Функции (1),(2),(3) называют конечномерными распределениями случайного процесса.

Построить такую систему функции для произвольного случайного процесса практически невозможно. Обычно случайные процессы задают с помощью априорных предположений о его свойствах, таких как независимость приращений, марковский характер траекторий и т. п.

Процесс, у которого все конечномерные распределения нормальны, называется нормальным (гауссовским). Оказывается, что для полного описания такого процесса достаточно знания одно- и двумерного распределений (1), (2), что важно с практической точки зрения, поскольку позволяет ограничиться исследованием математического ожидания и корреляционной функцией процесса.

В теории временных рядов используются ряд моделей случайной составляющей, начиная от простейшей – «белого шума», до весьма сложных типа авторегрессии – скользящего среднего и других, которые строятся на базе белого шума.

Прежде чем определять процесс белого шума рассмотрим последовательность независимых случайных величин, для которой функция распределения есть

Из последнего соотношения следует, что все конечномерные распределения последовательности определяются с помощью одномерных распределений.

Если к тому же в такой последовательности составляющие ее случайные величины X(t) имеют нулевое математическое ожидание и распределены одинаково при всех t Î T, то это – «белый шум». В случая нормальности распределения X(t) говорят о гауссовском белом шуме. Итак, гауссовский белый шум – последовательность независимых нормально распределенных случайных величин с нулевым математическим ожиданием и одинаковой (общей) дисперсией.

Более сложными моделями, широко используемыми в теории и практике анализа временных рядов, являются линейные модели: процессы скользящего среднего, авторегрессии и смешанные.

Процесс скользящего среднего порядка q представляет собой взвешенную сумму случайных возмущений:

(4),

где – независимые одинаково распределенные случайные величины (белый шум);

– числовые коэффициенты.

Легко видеть из определения, что у процесса скользящего среднего порядка q (сокращенно CC(q)) статистически зависимыми являются (q+1) подряд идущих величин X(t), X(t-1),..., X(t-q). Члены ряда, отстоящие друг от друга больше чем на (q+1) такт, статистически независимы, поскольку в их формировании участвуют разные слагаемые .

Процессом авторегрессии порядка p (сокращенно АР(р)) называют взвешенную возмущенную сумму p прошлых значений временного ряда

(5),

где – случайное возмущение, действующее в текущий момент t;

– числовые коэффициенты.

Выражая последовательно в соответствии с соотношением (5) X(t-1) через X(t-2), . . . , X(t-p-1), затем X(t-2) через X(t-3), . . . , X(t-p-2) и т.д. получим, что X(t) есть бесконечная сумма прошлых возмущений Из этого следует, члены процесса авторегрессии X(t) и X(t-k) статистически зависимы при любом k.

Процесс АР(1) часто называют процессом Маркова, АР(2) – процессом Юла. В общем случае марковским называют такой процесс, будущее которого определяется только его состоянием в настоящем и воздействиями на процесс, которые будут оказываться в будущем, тогда как его состояние до настоящего момента при этом несущественно. Процесс АР(1)

является марковским, поскольку его состояние в любой момент определяется через значения процесса , если известна величина в момент . Формально процесс авторегресси произвольного порядка также можно считать марковским, если его состоянием в момент t считать набор

(X(t),X(t-1), . . . , X(t-p-1)) .

Более полно модели СС, АР, а также их композиция: модели авторегрессии – скользящего среднего рассматриваются далее (п.10.1.5 ). Заметим только, что все они представляются частными случаями общей линейной модели

(6)

где – весовые коэффициенты, число которых, вообще-то говоря, бесконечно.

Среди моделей случайной составляющей выделим важный класс – стационарные процессы, такие, свойства которых не меняются во времени. Случайный процесс Y(t) называется стационарным, если для любых n, распределения случайных величин и одинаковы. Иными словами, функции конечномерных распределений не меняются при сдвиге времени:

Образующие стационарную последовательность случайные величины распределены одинаково, так что определенный выше процесс белого шума является стационарным.