Быстрый поиск

Реферат: Средства визуализации изображений в компьютерной томографии и цифровых рентгенографических системах

Функция g(a ,l ) есть интеграл от функции f(x) вдоль проходящего через точку Ф(l ) в направлении вектора a . Отметим, что при любом фиксированном l функция является l однородной функцией a степени -1:

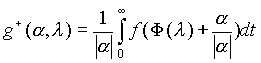. (2.1.1)

Для функций, имеющих финитный носитель, в [101] получена формула:

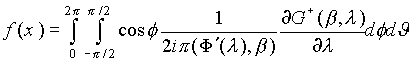. (2.1.2)

При фиксированном l функция G+(b ,l ) есть преобразование Фурье от функции по переменной a , b = (cosq cosf , sinq cosf , sinf ). В формуле (2.1.2) l зависит от x и b и выбирается из условий: скалярное произведение (b , x) равно (b ,f (l )), но (b ,Ф(l )) не равно нулю. Значение функции f(x) может быть восстановлено в точке x, если такое l существует для любого b . Геометрически это означает, что любая плоскость, пересекающая точку x носителя функции, пересекает кривую Ф(l ) так, что знаменатель в (2.1.2) не обращается в нуль. Примером кривой, удовлетворяющей условиям Кириллова-Туя, является совокупность двух единичных окружностей, лежащих во взаимно перпендикулярных плоскостях, если носитель лежит в единичном шаре. Для цилиндрических объектов можно использовать винтовую линию.

В формулу (2.1.2) входит G+(b ,l ) - преобразование Фурье от функции , однако преобразование Фурье, понимаемое в обычном смысле:

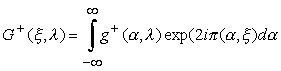в данном случае не существует, так как является однородной и имеет на бесконечности порядок 1/ê a ê . Преоразование Фурье здесь понимается в смысле обобщенных функций. Поскольку однородная функция, то при любом фиксированном l исходные данные, полностью определяются своими значениями на поверхности ê a ê =1. Переход к функции, заданной во всем пространстве R3 при использовании преобразования Фурье приводит к обобщенным функциям. Преобразование Фурье в смысле обобщенных функций является линейным функционалом над соответствующим пространством. Подробнее об этом будет сказано в следующих параграфах. Здесь нам важно отметить, что не любой функционал задается с помощью регулярной функции. Для того, чтобы использовать формулы типа (2) для построения алгоритмов, необходимо показать, что задается с помощью регулярной функции и иметь для нее выражения через функцию . В работе [101] дается выражение, связывающее , при x отличном от нуля с помощью регулярных операций с искомой функций f(x), то есть фактически показано, что функционал задается с помощью регулярной функции. Однако для построения алгоритмов томографической реконструкции нужно выразить не через искомую функцию f(x), а через исходные данные .

Итак, перейдем к нахождению . Мы будем использовать то, что является однородной функцией по a фиксированном l . В [95] доказано следующее

Утверждение: Пусть есть преобразование Фурье в смысле обобщенных функций от однородной функции , тогда

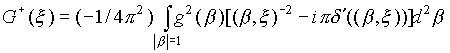. (2.1.3)

Строгое доказательство требует существенного использования аппарата обобщенных функций, понимаемых как линейные функционалы над соответствующим пространством. Здесь мы ограничимся изложением основных моментов доказательства. В частности, замену переменных в расходящихся интегралах мы будем делать по тем же правилам, что и в обычных.

Представим в виде

(поскольку параметр l фиксирован, его на данном этапе можно опустить).

Как уже отмечалось выше, интеграл является расходящимся, тем не менее, переходя к сферическим координатам по обычным правилам, получаем:

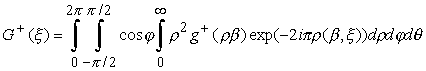где b = b (j ,q ) = (cosq cosj , sinq cosj , sinj ), j Î [-p /2, p /2], q Î [0, p ].

Учитывая, что , а также то, что интегрирование по углам j и q соответствует интегрированию по единичной сфере, приходим к выражению

Интеграл по r есть преобразование Фурье от r ++. Используя таблицы для преобразования Фурье обобщенных функций [19], приходим к выражению (2.1.3).

Для действительных функций f(x) в формуле (2) нужна мнимая часть :

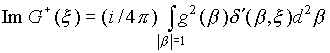Используя обобщенные функции, сосредоточенные на поверхности [19], получаем следующее следствие:

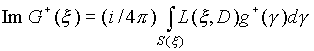Здесь S(x ) = {g Î S2½ (x , g ) = 0), 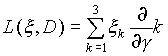v производная по направлению x . Подставляя в (2.1.2) функции и , зависящие от параметра l , получаем формулу обращения, пригодную для построения численных алгоритмов:

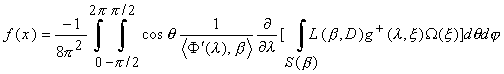(2.1.4)

Здесь S(x ) v окружность, являющаяся пересечением единичной сферы и плоскости P(b ). Плоскость P(b ) проходит через начало координат ортогональна вектору b . Символ W (x ) означает интегрирование по окружности. Оператор L(b , D) означает дифференцирование функции в направлении вектора b :

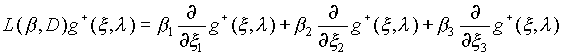при этом l , зависящее от b и x, остается фиксированным.

Как и выше, b = b (q , j ) = (cosq cosj , cosq sinj , sinq ), l = l (q , j ) = l (x, b ) такое, что скалярное произведение (x, b ) равно (b , g (l )) и (b , g /(l )).

В формуле (4) используются регулярные функции, и она пригодна для построения численных алгоритмов.

Замечание. А.С. Денисюком независимо и другим методом, без явного использования преобразования Фурье обобщенных функций, получены формулы обращения функции g+ в Rn . При n = 3 формулы А.С. Денисюка и формулы, получаемые изложенным способом из формулы Туя, совпадают.

Выше были получены формулы, позволяющие строить численные алгоритмы восстановления функции f(x) = f(x1, x2, x3) по ее лучевому преобразованию

Далее мы будем опускать символ f и использовать обозначение .

При фиксированном S функция является функцией в трехмерном пространстве, но в силу ee однородности существуют поверхности, такие что полностью определяется своими значениями на них (поверхности расположения приемников излучения).

Исходные данные в виде функции удобно использовать, если матрица приемников расположена на сфере. Однако в реальных ситуациях матрицу приемников обычно располагают на плоскости или поверхности цилиндра. В этих случаях удобно использовать несколько иной вид исходных данных.

Плоский детектор.

Мы будем предполагать, что для источника, находящегося в точке S = (s1, s2, s3), исходные данные регистрируются в плоскости P, определяемой уравнением xs1 + ys2 + zs3 = -½ S½ . Плоскость P, определяется следующими условиями:

плоскость P перпендикулярна лучу, соединяющему источник с началом координат;

плоскость P проходит через точку S= (s1, s2, s3.)

Расстояние D между плоскостью регистрации и источником равно удвоенному расстоянию от источника до начала координат. В плоскости регистрации будем использовать прямоугольную систему координат (p1, p2), начало которой находится в точке пересечения с лучем, соединяющим источник с точкой (0, 0, 0). Таким образом, если источник находится в точке S = (s1, s2, s3), то начало системы координат (p1, p2) в плоскости наблюдения находится в точке с трехмерными координатами -s1, -s2, -s3 =- S.

При реконструкции в конусе лучей наиболее распространенными примерами траекторий источника являются винтовая линия и совокупность двух окружностей лежащих в пересекающихся плоскостях.

Траектория в виде двух окружностей.

Рассмотрим окружность, лежащую в плоскости z =0.

Направление оси p2 в плоскости регистрации будет совпадать с направлением оси z.

Ось p1 системы координат возьмем на линии пересечения плоскости регистрации с плоскостью, содержащей окружность, по которой движется источник. Для окончательного определения системы координат необходимо выбрать одно из двух возможных направлений оси p1. Если s3 = 0, s1 = r cosl , s2 = r sinl (источник движется в плоскости z =0), то положительный единичный вектор на оси p1 выберем так, чтобы он совпадал с вектором (cos(l +p /2), sin(l +p /2), 0) = (-sinl , cosl , 0) = (-s2/½ S½ , s1/½ S½ , 0).

Точка, имеющая в плоскости регистрации координаты (p1, p2), имеет следующие пространственные координаты:

x = -p1 sinl - r cosl = -p1 s2 /½ S½ - s1 ,

y = p1 cos l - r sinl = p1 s1 /½ S½ - s2 , z = p2.

В случае плоского детектора, исходными данными являются интегралы по лучам, соединяющим точки (p1, p2) в плоскости регистрации с источником S.

Регистрируемая функция gr(p1, p2, l ) есть интеграл от искомой функции f(x) = f(x1, x2, x3) вдоль луча исходящего из точки S = (s1, s2, s3) = (rcosl , r sinl , 0) в направлении точки

P = (-p1 sin l - rcosl , p1 cosl - r sinl , p2 ) = (-p1 s2/½ S½ v s1, p1 s1/½ S½ v s2, p2).

Интегральная форма регистрируемой функции имеет вид:

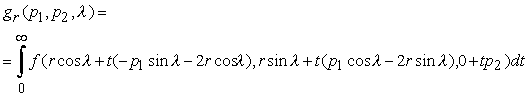
При t = 0 луч проходит через точку S = (rcosl , rsinl , 0), при t = 1 v через точку P = (p1, p2) = (-p1 sin l - rcosl , p1 cosl - r sinl , p2).

Итак, мы имеем соотношение между функциями gr(p1, p2, l ) и :

Наряду с обозначением gr(p1, p2, l ), мы будем использовать обозначения gr(p1, p2, S(l )), gr(p1, p2, S) и gr(P, S) , здесь S(l ) точка на траектории источника, соответствующая параметру l , P = (p1, p2). Мы выразили функцию gr(p1, p2, l ) через функцию = g+ (x , l ).

В формуле обращения лучевого преобразования используется функция g+ (x , l ) = для того, чтобы использовать gr(p1, p2, l ), регистрируемую в случае плоского детектора, нужно выразить g+ (x , l ) используя gr(p1, p2, l ).

Для дальнейшего нам потребуются координаты (p1, p2) (в системе координат плоскости регистрации) точки пересечения плоскости регистрации данных с лучем (S +tx ) = (s1 + tx 1, s2 + tx 2, s3 + tx 3). Эти координаты имеют вид:

Теперь мы можем выразить используя gr(p1, p2, l ):

= g+ (x , l ) = gr(2 ½ S(l )½ (s2(l )x 1 v s1(l )x 2) /, -2½ S(l )½ 2x 3 /,l ),

если < 0, = 0, если ³ 0.

Итак, мы имеем следующее соотношение между функциями:

g+ (P, l ) и = g+ (x , l ); P = (p1, p2), x = (x 1, x 2, x 3,);

= g+ (x , l ) =

= gr(2 ½ S(l )½ (s2(l )x 1 v s1(l )x 2) /, - 2½ S(l )½ 2x 3 /,l ),

если < 0,

= 0, если ³ 0.

При переходе от функции g+ (x , l ) = к функции gr (P, S) интегрирование по окружности S(l ) в трехмерном пространстве заменяется на интегрирование по прямым линиям в плоскости регистрации. Отметим, что формулы обращения лучевого преобразования, использующие интегрирование вдоль прямых в плоскости регистрации.

4.3 Элементы теории обобщенных функций в применении к задачам обращения лучевого преобразования

Обобщенная функция это непрерывный линейный функционал на пространстве К всех функций a (x), имеющих производные всех порядков и финитный носитель (свой для каждой из функций α (x)). Любая регулярная интегрируемая функция f(x) задает линейный функционал (f, a ):

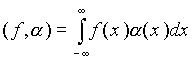. (2.2.1)

Однако на пространстве функций K существуют непрерывные линейные функционалы, которые не могут быть заданы с помощью регулярных интегрируемых функций, наиболее известными примерами таких функционалов являются δ-функция и ее производные. Другим широко известным примером является функционал, основанный на функции (1/x)dx. Функция 1/x x является регулярной, однако она не является интегрируемой. При задании соответствующего функционала интеграл

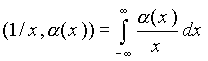(2.2.2)