Быстрый поиск

Реферат: Синтез комбинацонных схем и конечных автоматов, сети Петри

Таблица 2.3.5 – Новая общая таблица переходов.

На основании полученной общей таблицы переходов и выходов можно нарисовать граф минимизированного автомата с двумя состояниями:

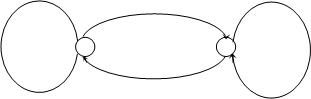0/1U 2/1 1/0 U 3/0 1/1U 3/1

0 1

0/0 U 2/0

Рисунок 2.3.1 – Граф минимизированного автомата

Для практической реализации полученного автомата надо двоично закодировать все сигналы. Для кодировки y и s достаточно одного двоичного разряда, x требует двух – x1 и x2:

x	x1	x2
0	0	0
1	0	1
2	1	0
3	1	1

Таблица 2.3.6 – Двоичная кодировка x

Составляем таблицу истинности для комбинационной части схемы на основе таблицы (2.3.5). Получаем две функции трёх аргументов:

x1(j)	0	0	0	0	1	1	1	1
x2(j)	0	0	1	1	0	0	1	1
s(j)	0	1	0	1	0	1	0	1
y(j)	1	0	0	1	1	0	0	1
s(j+1)	0	0	1	1	0	0	1	1

Таблица 2.3.7 – Таблица истинности комбинационной части

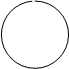
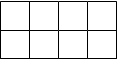
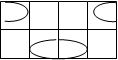
Каждую из функций y(j) и s(j+1) минимизируем с помощью карт Карно:

y(j) s(j+1)

x1(j)x2(j) x1(j)x2(j)

00 01 11 10 00 01 11 10

0 1 1 0 1 1

s(j) s(j)

1 1 1 1 1 1

Рисунок 2.3.2 – Карты Карно для комбинационной части

На основании выбранных покрытий записываем минимизированные выражения для функций переходов и выходов:

(2.3.2)

(2.3.3)

Реализуем полученные функции в виде комбинационной схемы, добавляя к ней элементы памяти – D - триггер и задержку. Комбинационную часть реализуем в базисе И – ИЛИ – НЕ.

Рисунок 2.3.2 – Схема минимизированного автомата в базисе И – ИЛИ – НЕ

2.3.4 Выводы по разделу

В этом разделе был показан пример минимизации (упрощения) конечного автомата с сокращением числа состояний, а также пример реализации автомата на логических элементах и элементах памяти. Мы убедились в том, что конечный автомат является расширением понятия комбинационной схемы на случай, когда для получения выходного сигнала в данный момент времени требуется “помнить” некоторое количество предыдущих значений входного сигнала, а не только его текущее значение. При практической реализации автомата стала очевидной польза проведённых операций по упрощению исходного автомата и приведению его комбинационной части к конкретному базису.

3 Сети Петри

3.1 Постановка задачи

Для заданной сети Петри, описывающей распределение ресурсов для случая двух процессов, сделать следующее:

а) выписать матричное уравнение смены маркировок;

б) построить дерево и граф покрываемости маркировок;

в) описать поведенческие свойства сети на основе графа покрываемости и матричных уравнений;

г) выписать множество достижимых из μ0 маркировок;

д) разработать программу моделирования сети Петри.

3.2 Теоретические сведения

Сети Петри – наиболее удачный из существующих математический аппарат для моделирования, анализа, синтеза и проектирования самых разных дискретных систем с параллельно протекающими процессами.

Определение. Сетью Петри называется четвёрка элементов

C = (P, T, I ,O), (3.2.1)

где

P = { p1, p2,…,pn }, n > 0 (3.2.2)

множество позиций (конечное),

T = { t1, t2,…,tm }, m > 0 (3.2.3)

множество переходов (конечное),

I: T → P (3.2.4)

функция входов (отображение множества переходов во входные позиции),

O: T → P (3.2.5)

функция выходов (отображение множества переходов в выходные позиции).

Если pi I (tj) , то pi – входная позиция j - го перехода, если pi I (tj) , то pi – выходная позиция j - го перехода.

Для наглядного представления сетей Петри используются графы.

Граф сети Петри есть двудольный ориентированный мультиграф

G = (V,), (3.2.6)

где V = P U T , причём P ∩ T = Ø.

Исходя из графического представления сети Петри, её можно определить и так:

C = (P, T, A), (3.2.7)

где А – матрица инцидентности графа сети.

Определим понятие маркированной сети Петри – оно является ключевым для любой сети.

Маркировка μ сети Петри C = (P, T, I, O) есть функция:

N = μ(P), N N, (3.2.8)

отображающая множество позиций на множество натуральных чисел. Маркировку можно также определить как вектор:

μ = {μ1, μ2,…, μn} , (3.2.9)

где n = │P │, а μi N. Между этими определениями есть связь:

μi = μ (pi) (3.2.10)

На графе маркировка отображается ссответствующим числом точек в каждой позиции. Точки называются маркерами или фишками. Если фишек много (больше трёх), то их количество отображается числом.

Таким образом, маркированная сеть Петри представляет собой пятёрку элементов:

M = (P, T, I, O, μ). (3.2.11)

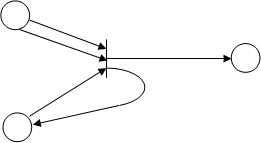
Пример простейшей сети Петри:

▪▪▪

t1 p3

p2 ▪

Рисунок 3.2.1 – Пример сети Петри

Правила работы с сетями Петри.

Сеть Петри выполняется посредством запуска переходов. Переход может быть запущен в том случае, когда он разрешён. Переход является разрешённым, если каждая из его входных позиций содержит число фишек не меньшее, чем число дуг из неё в данный переход.

Процедура запуска состоит в удалении из каждой входной позиции перехода числа фишек, равного числу дуг из неё, и в выставлении в каждой выходной позиции числа фишек, равного числу дуг, входящему в неё.

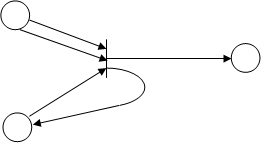
Проиллюстрируем сказанное на примере уже нарисованной сети Петри. Запустим в ней переход t1 – он является разрешённым:

▪

t1 p3

▪

p2 ▪

Рисунок 3.2.2 – Пример запуска перехода сети Петри

Пространство состояний и поведенческие свойства сетей Петри.

Пусть имеется маркированная сеть Петри:

M = (P, T, I, O, μ) (3.2.12)

У неё n позиций. В каждой позиции не более N фишек. Тогда пространство сотояний есть множество всех возможных маркировок сети. Определим δ – функцию следующего состояния.

Если переход tj разрешён при текущей маркировке μ , то следующая маркировка μ’ определится так:

μ’ = δ (μ, tj) (3.2.13)

Если переход tj не разрешён, то δ не определена.

Пусть {tj0, tj1,…, tjs} – последовательность запущенных переходов. Тогда ей будет соответствовать последовательность {μ0, μ1,…,μs+1}, то есть

μk+1 = δ(μk, tjk) (3.2.14)

На основании последнего равенства можно определить понятие непосредственно достижимой маркировки. Для сети C = (P, T, I ,O) маркировка μ’ называется непосредственно достижимой из μ , если существует такой переход tj T, при котором

μ' = δ(μ , tj) (3.2.15)

Можно распространить это понятие на множество достижимых из данной маркировок. Определим множество достижимых из μ маркировок R(C, μ) следующим образом:

во - первых, μ R(C, μ);

во - вторых, если μ’ R(C, μ), μ’ = δ(μ , tj) и μ’’ = δ(μ’, tk), то и μ’’ R(C, μ).

На основе введённых понятий можно сформулировать ряд свойств сети Петри, характеризующих её в процессе смены маркировок – назовём их поведенческими свойствами сети Петри. Определим наиболее важные из них.

1 Достижимость данной маркировки. Пусть имеется некоторая маркировка μ, отличная от начальной. Тогда возникает вопрос достижимости: можно ли путём запуска определённой поледовательности переходов перейти из начальной в заданную маркировку.

2 Ограниченность. Сеть Петри называется k- ограниченной, если при любой маркировке количество фишек в любой из позиций не превышает k. В частности, сеть называется безопасной, если k равно 1. Кроме того, сеть называется однородной, если в ней отсутствуют петли и одинарной (простой), если в ней нет кратных дуг.

3 Активность. Сеть Петри называется активной, если независимо от дотигнутой из μ0 маркировки существует последовательность запусков, приводящая к запуску этого перехода.

Реально вводят понятия нескольких уровней активности для конкретных переходов. Переход tj T называется:

а) пассивным (L0- активным), если он никогда не может быть запущен;

б) L1- активным, если он может быть запущен последовательностью переходов из μ0 хотя бы один раз;

в) L2- активным, если для любого числа K существует последовательность запусков переходов из μ0 , при которой данный переход может сработать K и более раз;

г) L3- активным, если он является L2- активным при K → ∞.

4 Обратимость. Сеть Петри обратима, если для любой маркировки μ R(C, μ0) маркировка μ0 достижима из μ.

5 Покрываемость. Маркировка μ покрываема, если существует другая маркировка μ’ R(C, μ0) такая, что в каждой позиции μ’ фишек не меньше, чем в позициях маркировки μ.