Реферат: СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ В ЛИНЕЙНОЙ ЗАДАЧЕ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ

2.3. Пример сингулярного разложения

Проведем преобразование Хаусхолдера на матрице ,

К первой компоненте первого столбца прибавляем норму первого столбца, получим . Пусть

Преобразованная матрица A2 вычисляется следующим образом. Для первого столбца имеем:

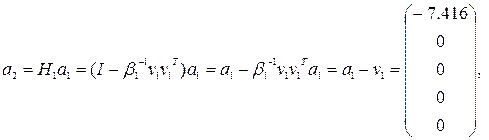
так как

Таким образом, в первый столбец были введены нули и его длина не изменилась. Получим второй столбец:

 

для третьего столбца:

окончательно,

Столбцы матрицы A2 получаются вычитанием кратных вектора v1 из столбцов A1. Эти кратные порождаются скалярными произведениями, а не отдельными элементами, как в гауссовом исключении.

Прежде чем вводить дальнейшие нули под диагональю, преобразованием вида A3=A2Q1, получают нули в первой строке. Нули уже стоящие в первом столбце, не должны быть испорчены, длина первого столбца должна быть сохранена; поэтому при внесении нулей в первую строку нельзя менять первый элемент строки, изменяем второй элемент и зануляем третий. Для матрицы большего размера на этом шаге было бы получено n–2 нуля.

Преобразование порождается первой строкой A2:

Строка матрицы A3 с номером i получается по формуле

.

Таким образом, из каждой строки A2 вычитается надлежащее кратное . Это дает матрицу

Поскольку первая компонента нулевая, то нули первого столбца A2 сохраняются в A3, Так как Q1 ортогональная, то длина каждой строки в A3 равна длине соответствующей строки в A2.

Теперь можно добиться новых нулей под диагональю, не испортив полученных ранее:

Поскольку ранг этой матрицы равен лишь 2, то теперь третий столбец имеет на диагонали и под диагональю  элементы порядка ошибки округления. Эти элементы обозначены в матрице через 0.000, чтобы отличить их от элементов, в точности равных нулю. Если бы матрица имела полный ранг, то нужно было бы выполнить еще одно преобразование, чтобы получить нули в третьем столбце:

Если бы не ошибки округлений, то в данном примере третий диагональный элемент был бы точным нулем. Элементы под диагональю во всех столбцах указаны как точные нули, потому что преобразования так и строились, чтобы получить там нули. Последнее преобразование H3 в этом примере могло бы быть тождественным, однако тогда оно не было бы хаусхолдеровым отражением. Фактически использование H3 попутно изменяет знак  элемента – 1.080 в матрице A4.

Получилась искомая двухдиагональная матрица, и первый этап закончен. Прямое использование ортогональных преобразований не позволяет получить какие–либо новые нули. Для общего порядка n нужно n преобразований H и n–2  преобразований Q, чтобы достигнуть данного места. Число преобразований не зависит от строчной размерности m, но от m зависит работа, затрачиваемая на выполнение каждого преобразования.

глава 3. Использование сингулярного разложения  в методе наименьших квадратов

При использовании метода сингулярного разложения (SVD – Singular Value Decomposition) мы проводим разложение для матрицы плана. При этом основное уравнение y=Xb приобретает вид y=USVTb. Отсюда следует, что коэффициенты b можно получить решая уравнение UTy=SVTb. Т.е. если все sj, j=1,…,n, являющиеся диагональными элементами S отличны от нуля, то последнее уравнение разрешимо и

, где .

Однако такое решение не всегда желательно, если некоторые sj малы. Для правильного использования метода SVD мы должны ввести границу t отражающую точность входных данных и точность использованной плавающей арифметики. Всякое sj, большее, чем t, приемлемо, и соответствующее  вычисляется по (1.20). Любое sj, меньшее, чем t, рассматривается как пренебрежимо малое, и соответствующему  может быть придано произвольное значение. С этой произвольностью значений связана не единственность набора коэффициентов, получаемых методом наименьших квадратов. Изменения входных данных и ошибки округлений, меньшие, чем t, могут привести к совершенно другому набору коэффициентов, определяемых этим методом. Поскольку обычно желательно, чтобы эти коэффициенты были по возможности малы, то полагаем =0, если sj £t.

Отбрасывание чисел sj, меньших, чем t, приводит к уменьшению числа обусловленности с  до . Поскольку число обусловленности является множителем в увеличении ошибки, то следствием будет более надежное определение коэффициентов .

Продемонстрируем использование метода на следующем примере:

t	Y
1900	75994575
1910	91972266
1920	105710620
1930	123203000
1940	131669275
1950	150697361
1960	179323175
1970	203211926

Следует определить значение Y при X =1980.

Если аппроксимировать эти данные квадратичным многочленом  и использовать двойную точность, то в результате получим следующие коэффициенты . При одинарной точности вычислений коэффициенты будут иметь значения . У этих двух наборов коэффициентов не совпадают даже знаки. Если такую модель использовать для предсказания, то для коэффициентов, вычисленных с двойной точностью, прогноз будет Y=227780000 , а для обычной точности Y=145210000. Ясно, что второй набор коэффициентов бесполезен. Исследуем достоверность результатов. Матрица плана для данного примера имеет размеры 8 ´ 3

Рис. 2. Численный пример

Ее сингулярные числа: .

Число обусловленности равно , что говорит о близости базисных функций 1, t и t2 к линейной зависимости. Для того, чтобы исправить ситуацию можно предпринять одну из следующих мер.

Во–первых, можно выбрать границу для относительной ошибки, которая бы отражала точность данных и точность арифметики. Если взять границу в интервале , то отбросим третье сингулярное число. При этом получим следующие наборы коэффициентов для двойной и обычной точности:

Теперь коэффициенты находятся в гораздо лучшем согласии друг с другом. Кроме того, коэффициенты стали существенно меньше, а это значит, что не будет столь большого, как прежде, взаимного уничтожения слагаемых при вычислении квадратичного многочлена. Прогнозное значение Y(1980) будет соответственно 212910000 и 214960000. Эффект обычной точности еще заметен, однако результаты уже не являются катастрофическими.

Можно также определить набор нулевых коэффициентов, соответствующих пренебрежимо малому сингулярному числу. Вот эти коэффициенты: . Для значений t от 1900 до 1970 величина функции  не превосходит 0.0017, поэтому при любом a коэффициенты можно изменить , и при этом значения, выдаваемые моделью изменятся не более чем на 0.0017a. Любой из четырех перечисленных нами наборов коэффициентов можно получить из другого подобным изменением.

Во–вторых, можно улучшить ситуацию заменой базиса. Модели

гораздо более удовлетворительны. Важно при этом то, что независимая переменная преобразуется из интервала [1900, 1970] в какой–нибудь более приемлемый интервал вроде [0, 70] или, еще лучше, [–3.5, 3.5]. Числа обусловленности при этом равны 5750 и 10.7 соответственно. последнее значение более чем приемлемо даже при счете с обычной точностью.

Удобнее всего воспользоваться стандартными способами статистического анализа, т.е. матрицу плана преобразуем к стандартизованному варианту Матрица стандартизованных данных есть матрица наблюдений с нулевым средним и дисперсией 1. Это означает, что данные берутся в виде отклонений от среднего, которое мы считаем равным 0, вводим нормировку деля каждый член столбца матрицы на корень квадратный из суммы квадратов отклонений.

Во втором случае, после преобразования матрицы плана ее обусловленность сильно уменьшается, и, соответственно, повышается точность расчетов.

Данную программу можно использовать и при решении системы линейных уравнений вместо методов Гаусса, Жордана, Холесского и пр. В приложении 2 приведен пример расчета линейной системы, которая изначально не может быть решена этими методами вследствие вырожденности матрицы коэффициентов. Тем не менее, исследуемый метод дает нам правильное решение.

ЗАКЛЮЧЕНИЕ

В работе описаны компьютерные методы решения задачи наименьших квадратов. Для использования данных методов составлена соответствующая программа на алгоритмическом языке FORTRAN. Программа апробирована, результаты тестирования показывают работоспособность программы.

Результаты данной разработки могут быть использованы в самых разнообразных расчетах, где необходимо провести аппроксимацию данных заданными функциями.

ЛИТЕРАТУРА

1.       Беллман Р. Введение в теорию матриц. -М.: Наука, 1969, 368с.

2.       Гантмахер Ф.Р. Теория матриц. -М.: Наука, 1988, 548с.

3.       Ланкастер П. Теория матриц. -М.: Наука, 1982, 387с.

4.       Лоусон Ч., Хенсон Р. Численное решение задач наименьших квадратов. М.: Статистика, 1979, 447с

5.       Марчук Г.И. Методы вычислительной математики. М.: Наука, 1980

6.       Мэйндоналд Дж. Вычислительные алгоритмы в прикладной статистике. М.: Финансы и статистика, 1988, 350с

7.       Стренг Г. Линейная алгебра и ее применения. М.: Мир, 1980, 454с

8.       Уилкинсон Дж., Райнш К. Справочник алгоритмов на языке АЛГОЛ. Линейная алгебра, М.: Машиностроение, 1976, 390с

9.       Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. -М.: Физматгиз, 1963, 536с.

10.    Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений. М.: Мир, 1980, 279с

11.    Харебов К.С. Компьютерные методы решения задачи наименьших квадратов и проблемы собственных значений. Владикавказ.: Изд-во СОГУ, 1995, 76 с.

ПРИЛОЖЕНИЕ 1. Исходные тексты программы

                REAL A(3,3), U(3,3), V(3,3), SIGMA(3), WORK(3),Y(3),C(3),Y0(3)

                INTEGER I,IERR, J, M, N, NM

                OPEN (6,FILE="SVD.OUT",STATUS="UNKNOWN",FORM="FORMATTED")

        OPEN (5,FILE= "SVD.IN",STATUS="UNKNOWN",FORM="FORMATTED")

140     FORMAT(3I5)

150     FORMAT(4E15.7)

        READ(5,140) NM,M,N

        DO 131 I=1,M

        READ(5,150) (A(I,J),J=1,N)

131     CONTINUE

        READ (5,150) (Y(I),I=1,M)

                CALL SVD(NM,M,N,A,SIGMA,.TRUE.,U,.TRUE.,V,IERR,WORK)

                IF(IERR.NE.0) WRITE (6,2) IERR

2             FORMAT(15H TROUBLE.IERR=,I4)

        WRITE(6,120)

120     FORMAT(/'МАТРИЦА А')

        DO 121 I=1,M

        WRITE(6,130) (A(I,J),J=1,N)

130     FORMAT(8E15.7)

121     CONTINUE

        WRITE (6,160) (Y(I),I=1,N)

160     FORMAT(/'ПРАВЫЕ ЧАСТИ'/8E15.7)

210     FORMAT(/'СИНГУЛЯРНЫЕ ЧИСЛА')

        WRITE(6,210)

                DO 3 J=1,N

                WRITE(6,6) SIGMA(J)

3             CONTINUE

        SMA=SIGMA(1)

        SMI=SIGMA(1)

        DO 211 J=2,N

        IF(SIGMA(J).GT.SMA) SMA=SIGMA(J)

        IF(SIGMA(J).LT.SMI.AND.SIGMA(J).GT.0.) SMI=SIGMA(J)

211     CONTINUE

        OBU=SMA/SMI

230     FORMAT(/'ЧИСЛО ОБУСЛОВЛЕННОСТИ=',E15.7)

        WRITE(6,230) OBU

        SIGMA1=0.

        DO 30 J=1,N

        IF(SIGMA(J) .GT. SIGMA1) SIGMA1=SIGMA(J)

        C(J)=0.

30      CONTINUE

        TAU=SIGMA1*0.1E-6

        DO 60 J=1,N

        IF(SIGMA(J).LE.TAU) GO TO 60

        S=0.

        DO 40 I=1,N

        S=S+U(I,J)*Y(I)

40      CONTINUE    

        S=S/SIGMA(J)

        DO 50 I=1,N

        C(I)=C(I) + S*V(I,J)

50      CONTINUE

60      CONTINUE

                write (6,560)

        WRITE (6,6) (C(I),I=1,3)

        DO 322 J=1,N

        SS=0.

        DO 321 I=1,M

321     SS=A(J,I)*C(I)+SS

322     Y0(J)=SS

                write (6,570)

        WRITE (6,6) (Y0(I),I=1,3)

C             WRITE(6,7)

C             DO 4 I=1,M

C             WRITE(6,6) (U(I,J),J=1,N)

C4          CONTINUE

C             WRITE(6,7)

C             DO 5 I=1,N

C             WRITE(6,6) (V(I,J),J=1,N)

C5          CONTINUE

6             FORMAT(3E15.7)

560         format(2x,'roots')

570         format(2x,'right')

7             FORMAT(1H )

                STOP

                E N D

SUBROUTINE SVD(NM,M,N,A,W,MATU,U,MATV,V,IERR,RV1)

        REAL A(NM,N),W(N),U(NM,N),V(NM,N),RV1(N)

        LOGICAL MATU,MATV

        IERR=0

        DO 100 I=1,M

        DO 100         J=1,N                    

        U(I,J)=A(I,J)

100     CONTINUE

                G=0.0

                SCALE=0.0

                ANORM=0.0

                DO 300 I=1,N

                L=I+1

                RV1(I)=SCALE*G

                G=0.0

                S=0.0

                SCALE=0.0

                IF(I.GT.M) GO TO 210

                DO 120 K=I,M

120         SCALE=SCALE+ABS(U(K,I))

                IF(SCALE.EQ.0.0) GO TO 210

                DO 130 K=I,M

                U(K,I)=U(K,I)/SCALE

                S=S+U(K,I)**2

130     CONTINUE

                F=U(I,I)

                G=-SIGN(SQRT(S),F)

                H=F*G-S

                U(I,I)=F-G

                IF(I.EQ.N) GO TO 190

                DO 150 J=L,N

                S=0.0

                DO 140 K=I,M

140         S=S+U(K,I)*U(K,J)

                F=S/H

                DO 150 K=I,M

                U(K,J)=U(K,J)+F*U(K,I)

150         CONTINUE

190     DO 200 K=I,M

200         U(K,I)=SCALE*U(K,I)

210         W(I)=SCALE*G

                G=0.0

                S=0.0

                SCALE=0.0

                IF(I.GT.M.OR.I.EQ.N) GO TO 290

                DO 220 K=L,N

220         SCALE=SCALE+ABS(U(I,K))

                IF(SCALE.EQ.0.0) GO TO 290

                DO 230 K=L,N

                U(I,K)=U(I,K)/SCALE

                S=S+U(I,K)**2

230         CONTINUE

                F=U(I,L)

                G=-SIGN(SQRT(S),F)

                H=F*G-S

                U(I,L)=F-G

                DO 240 K=L,N

240         RV1(K)=U(I,K)/H

                IF(I.EQ.M) GO TO 270

                DO 260 J=L,M

                S=0.0

                DO 250 K=L,N

250         S=S+U(J,K)*U(I,K)

                DO 260 K=L,N

                U(J,K)=U(J,K)+S*RV1(K)

260         CONTINUE

270         DO 280 K=L,N

280         U(I,K)=SCALE*U(I,K)

290         ANORM=AMAX1(ANORM,ABS(W(I))+ABS(RV1(I)))

300         CONTINUE

                IF(.NOT.MATV) GO TO 410

                DO 400 II=1,N

                I=N+1-II

                IF(I.EQ.N) GO TO 390

                IF(G.EQ.0.0) GO TO 360

                DO 320 J=L,N

320         V(J,I)=(U(I,J)/U(I,L))/G

                DO 350 J=L,N

                S=0.0

                DO 340 K=L,N

340         S=S+U(I,K)*V(K,J)

                DO 350 K=L,N

                V(K,J)=V(K,J)+S*V(K,I)

350         CONTINUE

360         DO 380 J=L,N

                V(I,J)=0.0

                V(J,I)=0.0

380         CONTINUE

390         V(I,I)=1.0

                G=RV1(I)

                L=I

400         CONTINUE

410         IF(.NOT.MATU) GO TO 510

                MN=N

                IF(M.LT.N) MN=M

                DO 500 II=1,MN

                I=MN+1-II

                L=I+1

                G=W(I)

                IF(I.EQ.N) GO TO 430

                DO 420 J=L,N

420         U(I,J)=0.0

430         IF(G.EQ.0.0) GO TO 475

                IF(I.EQ.MN) GO TO 460

                DO 450 J=L,N

                S=0.0

                DO 440 K=L,M

440         S=S+U(K,I)*U(K,J)

                F=(S/U(I,I))/G

                DO 450 K=I,M

                U(K,J)=U(K,J)+F*U(K,I)

450         CONTINUE

460         DO 470 J=I,M

470         U(J,I)=U(J,I)/G

                GO TO 490

475         DO 480 J=I,M

480         U(J,I)=0.0

490         U(I,I)=U(I,I)+1.0

500         CONTINUE

510         DO 700 KK=1,N

                K1=N-KK

                K=K1+1

                ITS=0

520         DO 530 LL=1,K

                L1=K-LL

                L=L1+1

                IF(ABS(RV1(L))+ANORM.EQ.ANORM) GO TO 565

                IF(ABS(W(L1))+ANORM.EQ.ANORM) GO TO 540

530         CONTINUE

540         C=0.0

        S=1.0

        DO 560 I=L,K

                F=S*RV1(I)

                RV1(I)=C*RV1(I)

                IF(ABS(F)+ANORM.EQ.ANORM) GO TO 565

                G=W(I)

                H=SQRT(F*F+G*G)

                W(I)=H

                C=G/H

                S=-F/H

                IF(.NOT.MATU) GO TO 560

                DO 550 J=1,M

                Y=U(J,L1)

                Z=U(J,I)

                U(J,L1)=Y*C+Z*S

                U(J,I)=-Y*S+Z*C

550         CONTINUE

560         CONTINUE

565         Z=W(K)

                IF(L.EQ.K) GO TO 650

                IF(ITS.EQ.30) GO TO 1000

                ITS=ITS+1

                X=W(L)

                Y=W(K1)

                G=RV1(K1)

                H=RV1(K)

                F=((Y-Z)*(Y+Z)+(G-H)*(G+H))/(2.0*H*Y)

                G=SQRT(F*F+1.0)

                F=((X-Z)*(X+Z)+H*(Y/(F+SIGN(G,F))-H))/X

                C=1.0

                S=1.0

                DO 600 I1=L,K1

                I=I1+1

                G=RV1(I)

                Y=W(I)

                H=S*G

                G=C*G

                Z=SQRT(F*F+H*H)

                RV1(I1)=Z

                C=F/Z

                S=H/Z

                F=X*C+G*S

                G=-X*S+G*C

                H=Y*S

                Y=Y*C

                IF(.NOT.MATV) GO TO 575

                DO 570 J=1,N

                X=V(J,I1)

                Z=V(J,I)

                V(J,I1)=X*C+Z*S

                V(J,I)=-X*S+Z*C

570         CONTINUE

575         Z=SQRT(F*F+H*H)

                W(I1)=Z

                IF(Z.EQ.0.0) GO TO 580

                C=F/Z

                S=H/Z

580         F=C*G+S*Y

                X=-S*G+C*Y

        IF(.NOT.MATU) GO TO 600

                DO 590 J=1,M

                Y=U(J,I1)

                Z=U(J,I)

                U(J,I1)=Y*C+Z*S

                U(J,I)=-Y*S+Z*C

590         CONTINUE

600         CONTINUE

        RV1(L)=0.0

                RV1(K)=F

                W(K)=X

                GO TO 520

650         IF(Z.GE.0.0) GO TO 700

                W(K)=-Z

                IF(.NOT.MATV) GO TO 700

                DO 690 J=1,N

690         V(J,K)=-V(J,K)

700         CONTINUE

                GO TO 1001

1000      IERR=K

1001      RETURN

                E N D

ПРИЛОЖЕНИЕ 2. контрольный пример

Входные данные

(матрица изначально сингулярна – первая строка равна сумме второй и третьей с обратным знаком)

3    3    3

   .3200000E 02   .1400000E 02   .7400000E 02

 -0.2400000E 02 -0.1000000E 02 -0.5700000E 02

 -0.8000000E 01 -0.4000000E 01 -0.1700000E 02

 -0.1400000E 02  0.1300000E 02  0.1000000E 01

Полученный результат

МАТРИЦА А

   .3200000E+02   .1400000E+02   .7400000E+02

  -.2400000E+02  -.1000000E+02  -.5700000E+02

  -.8000000E+01  -.4000000E+01  -.1700000E+02

ПРАВЫЕ ЧАСТИ

  -.1400000E+02   .1300000E+02   .1000000E+01

СИНГУЛЯРНЫЕ ЧИСЛА

   .1048255E+03

   .7310871E-06

   .1271749E+01

ЧИСЛО ОБУСЛОВЛЕННОСТИ=   .1433830E+09

  Корни

   .1215394E+01   .1821742E+01  -.1059419E+01

  Правые корни после проверки

  -.1400000E+02   .1300000E+02   .1000001E+01

Видно, что правые части соответствуют начальным данным. Решение верно.

[1] Матрица А эрмитова  если она совпадает со своей комплексно сопряженной .

[2] Матрица А унитарная  если , где  – сопряженная матрица.

[3] Сингулярным разложением произвольной m´n–матрицы называется разложение вида , где U и V – ортогональные матрицы, а S – диагональная матрица с неотрицательными диагональными элементами. Диагональные элементы S (, i=1,...,k, где k=min(m,n)) называются сингулярными числами А. Это множество чисел однозначно определяется матрицей А. Число ненулевых сингулярных чисел равно рангу А.

[4] Симметричная матрица положительно определена, если все ее собственные значения положительны. Положительно определенная матрица P обладает также тем свойством, что  для всех .

[5] Симметричная матрица неотрицательно определена, если все ее собственные значения неотрицательны. Такая матрица P обладает также тем свойством, что  для всех . Для произвольной mxn–матрицы А матрица  симметрична и неотрицательно определена. Она положительно определена, если rankA=n.

[6] Обратной матрицей  для квадратной невырожденной матрицы А называется такая матрица, для которой .

[7] Матрица перестановки - это квадратная матрица, столбцы которой получаются перестановкой столбцов единичной матрицы. Матрица перестановки ортогональна.

[8] Матрица А хессенбергова (верхняя хессенбергова) если  для j<i–1 (сохраняется одна диагональ ниже главной диагонали). Если матрица симметричная то хессенбергова матрица становится трехдиагональной.

[9] Симметричная матрица А есть трехдиагональная при  для |i-j|>1. Трехдиагональная матрица – это частный случай хесенберговой матрицы.