Быстрый поиск

Реферат: Разработка и исследование имитационной модели разветвленной СМО (системы массового обслуживания) в среде VB5

Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по несколько сразу. Например, поток клиентов, направляющихся в парикмахерскую или к зубному врачу, обычно ординарен, чего нельзя сказать о потоке клиентов, направляющихся в загс для регистрации брака. Поток поездов, подходящих к станции, ординарен, а поток вагонов — неординарен. Если поток событий ординарен, то вероятностью попадания на малый интервал времени t двух или более событий можно пренебречь.

Поток событий называется простейшим (или стационарным пуассоновским), если он обладает сразу тремя свойствами: стационарен, ординарен и не имеет последействия. Название «простейший» связано с тем, что процессы, связанные с простейшими потоками, имеют наиболее простое математическое описание. Самый простой, на первый взгляд, регулярный поток не является «простейшим», так как обладает последействием: моменты появления событий в таком потоке связаны жесткой функциональной зависимостью.

Простейший поток играет среди других потоков особую роль. А именно, при наложении (суперпозиции) достаточно большого числа независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивности) получается поток, близкий к простейшему.

Для простейшего потока с интенсивностью l интервал между соседними событиями имеет так называемое экспоненциальное распределение с плотностью

(t > 0) (1)

Величина l в формуле (1) называется параметром показательного закона. Для случайной величины Т, имеющей экспоненциальное распределение, математическое ожидание mT есть величина, обратная параметру, а среднее квадратическое отклонение sT равно математическому ожиданию:

(2)

В теории вероятностей в качестве «меры случайности» неотрицательной случайной величины нередко рассматривают так называемый коэффициент вариации:

(3)

Из формул (2), (3) следует, что для показательного распределения nt = 1, т. е. для простейшего потока событий коэффициент вариации интервалов между событиями равен единице.

Очевидно, что для регулярного потока событий, у которого интервал между событиями вообще не случаен (nt = 0), коэффициент вариации равен нулю. Элементом вероятности называется вероятность попадания на этот интервал хотя бы одного события потока. Легко доказать, что элемент вероятности (с точностью до малых величин более высокого порядка по сравнению с Dt) равен:

(4)

т. е. для простейшего потока элемент вероятности равен интенсивности потока, умноженной на длину элементарного интервала. Элемент вероятности, в силу отсутствия последействия, совершенно не зависит от того, сколько событий и когда появлялись ранее.

Нормальное распределение занимает центральное место среди непрерывных распределений. Его плотность определяется формулой:

F(t) = 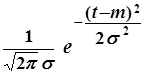(5)

где s > 0, m — параметры распределения. При s = 1 и m = 0 имеет место стандартное нормальное распределение с плотностью:

F(t) = 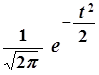(6)

Пусть рассматривается система S, имеющая n возможных состояний S1, S2, ..., Sn. Назовем вероятностью i-го состояния вероятность pi(t) того, что в момент t система будет находиться в состоянии Si. Очевидно, что для любого момента сумма всех вероятностей состояний равна единице.

Имея в своем распоряжении размеченный граф состояний, можно найти все вероятности состояний pi(t) как функции времени. Для этого составляются и решаются так называемые уравнения Колмогорова — дифференциальные уравнения особого вида, в которых неизвестными функциями являются вероятности состояний.

Что будет происходить с вероятностями состояний при t ® ¥ ? Будут ли p1(t), p2(t),... стремиться к каким-то пределам? Если эти пределы существуют и не зависят от начального состояния системы, то они называются финальными вероятностями состояний. В теории случайных процессов доказывается, что если число n состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое, то финальные вероятности существуют.

Финальную вероятность состояния Si можно истолковать как среднее относительное время пребывания системы в этом состоянии.

Граф состояний для схемы гибели и размножения имеет вид, показанный на рис. 1. Особенность этого графа в том, что все состояния системы можно вытянуть в цепочку, в которой каждое из средних состояний связано прямой и обратной стрелкой с каждым из соседних состояний — правым и левым, а крайние состояния — только с одним соседним состоянием. Термин «схема гибели и размножения» ведет начало от биологических задач, где подобной схемой описывается изменение численности популяции.

Схема гибели и размножения

l01 l12 l23 lk-1,k lk,k+1 ln-1,n

...

Sn-1

l10 l21 l32 lk,k-1 lk+1,k ln,n-1

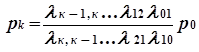
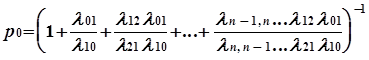
l — интенсивность потока; p0, pk — финальные вероятности состояний

Формулы Литтла

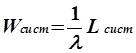Lсист — среднее число заявок в системе;

Wсист — среднее время пребывания заявки в системе;

WочL оч Lоч — среднее число заявок в очереди;

Wоч — среднее время пребывания заявки в очереди

m — интенсивность потока обслуживаний; l — интенсивность потока заявок

l /m = r (приведенная интенсивность потока заявок)

r — среднее число заявок, приходящее за среднее время обслуживания одной заявки

рис. 1

2.2 Классификация систем массового обслуживания

При исследовании операций часто приходится сталкиваться с работой систем массового обслуживания. СМО могут быть одноканальными и многоканальными.

Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем; состояние СМО меняется скачком в моменты появления каких-то событий (прихода новой заявки, окончания обслуживания, момента, когда заявка, которой «надоело ждать», покидает очередь).

Предмет теории массового обслуживания — построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, правила работы, характер потока заявок) с интересующими нас характеристиками — показателями эффективности СМО, описывающими, с той или другой точки зрения, ее способность справляться с потоком заявок. В качестве таких показателей (в зависимости от обстановки и целей исследования) могут применяться разные величины, например: среднее число заявок, обслуживаемых СМО в единицу времени; среднее число занятых каналов; среднее число заявок в очереди и среднее время ожидания обслуживания; вероятность того, что число заявок в очереди превысит какое-то значение, простои, и т. д.

Математический анализ работы СМО очень упрощается, если процесс этой работы — марковский. Для этого достаточно, чтобы все потоки событий, переводящие систему из состояния в состояние (потоки заявок, «потоки обслуживания»), были простейшими. Если это свойство нарушается, то математическое описание процесса становится гораздо сложнее и довести его до явных, аналитических формул удается лишь в редких случаях. Однако аппарат простейшей, марковской теории массового обслуживания может пригодиться для приближенного описания работы СМО даже в тех ситуациях, когда потоки событий — не простейшие. Во многих случаях для принятия разумного решения по организации работы СМО вовсе и не требуется точного знания всех ее характеристик — зачастую достаточно и приближенного, ориентировочного.

Системы массового обслуживания делятся на типы (или классы) по ряду признаков. Первое деление: СМО с отказами и СМО с очередью. В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем процессе обслуживания не участвует. Примеры СМО с отказами встречаются в телефонии: заявка на разговор, пришедшая в момент, когда все каналы связи заняты, получает отказ и покидает СМО необслуженной. В СМО с очередью заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь и ожидает возможности быть обслуженной. На практике чаще встречаются (и имеют большее значение) СМО с очередью; недаром теория массового обслуживания имеет второе название: «теория очередей».

СМО с очередью подразделяются на разные виды, в зависимости от того, как организована очередь — ограничена она или не ограничена. Ограничения могут касаться как длины очереди, так и времени ожидания (так называемые «СМО с нетерпеливыми заявками»). При анализе СМО должна учитываться также и «дисциплина обслуживания» — заявки могут обслуживаться либо в порядке поступления (раньше пришла, раньше обслуживается), либо в случайном порядке. Нередко встречается так называемое обслуживание с приоритетом — некоторые заявки обслуживаются вне очереди. Приоритет может быть как абсолютным — когда заявка с более высоким приоритетом «вытесняет» из-под обслуживания заявку с низшим, так и относительным — когда начатое обслуживание доводится до конца, а заявка с более высоким приоритетом имеет лишь право на лучшее место в очереди.

Существуют СМО с так называемым многофазовым обслуживанием, состоящим из нескольких последовательных этапов или «фаз» (например, покупатель, пришедший в магазин, должен сначала выбрать товар, затем оплатить его в кассе, после чего получить на контроле).

Кроме этих признаков, СМО делятся на два класса: «открытые» и «замкнутые». В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии находится сама СМО (сколько каналов занято). В замкнутой СМО — зависят. Например, если один рабочий обслуживает группу станков, время от времени требующих наладки, то интенсивность потока «требований» со стороны станков зависит от того, сколько их уже неисправно и ждет наладки. Это — пример замкнутой СМО.

Рассмотрим вывод упомянутой ранее формулы Литтла, связывающей (для предельного, стационарного режима) среднее число заявок Lсист, находящихся в системе массового обслуживания (т. е. обслуживаемых или стоящих в очереди), и среднее время пребывания заявки в системе Wсист.

Рассмотрим любую СМО (одноканальную, многоканальную, марковскую, немарковскую, с неограниченной или с ограниченной очередью) и связанные с нею два потока событий: поток заявок, прибывающих в СМО, и поток заявок, покидающих СМО. Если в системе установился предельный, стационарный режим, то среднее число заявок, прибывающих в СМО за единицу времени, равно среднему числу заявок, покидающих ее, так как оба потока имеют одну в ту же интенсивность l.

Обозначим: X(t)—число заявок, прибывших в СМО до момента t, Y(t) — число заявок, покинувших СМО до момента t. И та, и другая функции являются случайными и меняются скачком (увеличиваются на единицу) в моменты приходов заявок (X(t)) и уходов заявок (Y(t)). Для любого момента t их разность Z(t) = X(t) - Y(t) — это число заявок, находящихся в СМО.

Рассмотрим очень большой промежуток времени T и вычислим для него среднее число заявок, находящихся в СМО. Оно будет равно интегралу от функции Z(t) на этом промежутке, деленному на длину интервала T:

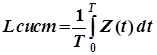(7)

Данный интеграл представляет собой площадь фигуры, заключенной между X(t) и Y(t). Фигура состоит из прямоугольников, каждый из которых имеет высоту, равную единице, и основание, равное времени пребывания в системе соответствующей заявки (первой, второй и т. д.). Обозначим эти времена как t1, t2,... Правда, под конец промежутка Т некоторые прямоугольники войдут в эту фигуру не полностью, а частично, но при достаточно большом Т этим можно пренебречь. Таким образом, можно считать, что

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15