 Реферат: Морфологический анализ цветных (спектрозональных) изображений
Реферат: Морфологический анализ цветных (спектрозональных) изображений
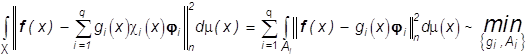 . (28)
. (28)
Рассмотрим вначале задачу (28) не
требуя, чтобы ![]() . Так как для
любого измеримого
. Так как для
любого измеримого ![]()
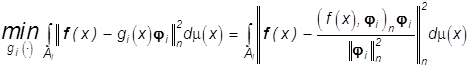 , (29)
, (29)
и достигается на
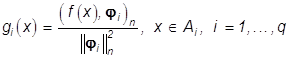 , (30)
, (30)
то, как нетрудно убедиться,
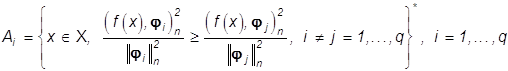 , (31)
, (31)
где звездочка * означает то же самое, что и в
равенстве (14): точки xÎX, в которых
выполняется равенство 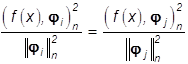 могут
быть произвольно отнесены к одному из множеств Ai или Aj.
могут
быть произвольно отнесены к одному из множеств Ai или Aj.
Пусть
![]() - разбиение
- разбиение ![]() , в котором
, в котором
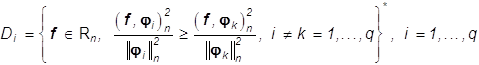 (32)
(32)
а F: Rn-> Rn оператор, определенный условием
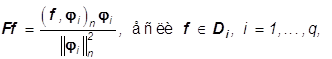 (33)
(33)
Тогда решение задачи (28) можно представить в виде
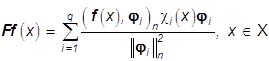 , (34)
, (34)
где ![]() -
индикаторная функция множества Ai (31), i=1,...,q и F
-оператор, действующий в
-
индикаторная функция множества Ai (31), i=1,...,q и F
-оператор, действующий в ![]() по
формуле (34) (см. сноску 4 на стр. 13).
по
формуле (34) (см. сноску 4 на стр. 13).
Нетрудно убедиться, что задача на
минимум (29) с условием физичности ![]()
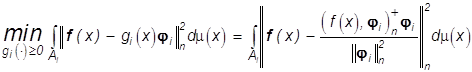 (35)
(35)
имеет решение
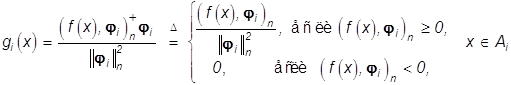 (36)
(36)
Соответственно решение задачи (28) с условием физичности имеет вид
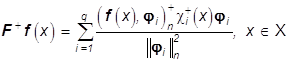 , (37)
, (37)
где ![]() -
индикаторная функция множества
-
индикаторная функция множества
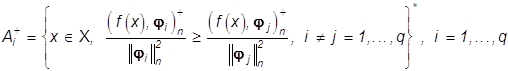 , (38)
, (38)
В ряде случаев для построения (34) полезно определить оператор F+: Rn-> Rn, действующий согласно формуле
 (39)
(39)
где
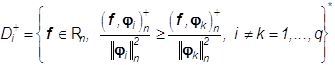 , так что
, так что ![]() ,i=1,...q. (40)
,i=1,...q. (40)
Подытожим сказанное.
Теорема 4. Решение задачи (28)
наилучшего в ![]() приближения
изображения
приближения
изображения ![]() изображениями
на искомых множествах A1,...,Aq разбиения X заданные цветами
j1,..., jq соответственно, дается равенством (34), искомое разбиение A1,...,Aq
определено в (31). Требование физичности
наилучшего приближения приводит к решению (37) и определяет искомое
разбиение формулами (38). Решение (34) инвариантно относительно
любого, а (37) - относительно любого, сохраняющего физичность,
преобразования, неизменяющего его цвет.
изображениями
на искомых множествах A1,...,Aq разбиения X заданные цветами
j1,..., jq соответственно, дается равенством (34), искомое разбиение A1,...,Aq
определено в (31). Требование физичности
наилучшего приближения приводит к решению (37) и определяет искомое
разбиение формулами (38). Решение (34) инвариантно относительно
любого, а (37) - относительно любого, сохраняющего физичность,
преобразования, неизменяющего его цвет.
Формой в широком смысле
изображения, имеющего заданный набор цветов j1,..., jq на некоторых множествах
положительной меры A1,...,Aq разбиение поля зрения можно назвать оператор ![]() (34),
формой такого изображения является оператор F+ (37). Всякое
такое изображение g(×), удовлетворяющее условиям физичности (неотрицательности
яркостей), удовлетворяет уравнению F+g(×)=g(×), те
из них, у которых m(Ai)>0, i=1,...,q, изоморфны, остальные
имеют более простую форму. n
(34),
формой такого изображения является оператор F+ (37). Всякое
такое изображение g(×), удовлетворяющее условиям физичности (неотрицательности
яркостей), удовлетворяет уравнению F+g(×)=g(×), те
из них, у которых m(Ai)>0, i=1,...,q, изоморфны, остальные
имеют более простую форму. n
В заключение этого раздела вернемся
к понятию формы изображения, заданного с точностью до произвольного,
удовлетворяющего условиям физичности, преобразования яркости. Речь идет о форме
изображения ![]() , заданного распределением
цвета
, заданного распределением
цвета ![]() , при произвольном
(физичном) распределении яркости, например,
, при произвольном
(физичном) распределении яркости, например, ![]() .
Для определения формы
.
Для определения формы ![]() рассмотрим задачу
наилучшего в
рассмотрим задачу
наилучшего в ![]() приближения изображения
приближения изображения ![]() такими изображениями
такими изображениями
![]() , (41)
, (41)
Теорема 5. Решение ![]() задачи (41) дается
равенством
задачи (41) дается
равенством
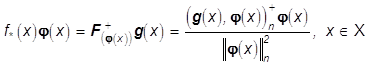 , (42)
, (42)
в котором 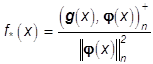 , где
, где
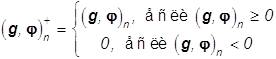 . Невязка приближения
. Невязка приближения
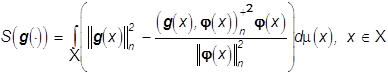 , (43)
, (43)
( ![]() !) n
!) n
Определение. Формой
изображения, заданного распределением цвета ![]() ,
назовем выпуклый, замкнутый конус изображений
,
назовем выпуклый, замкнутый конус изображений
![]()
или - проектор ![]() на
на
![]() .
.
Всякое изображение g(×),
распределение цвета которого есть j(×) и только такое изображение содержится
в ![]() и является неподвижной
точкой оператора
и является неподвижной
точкой оператора
![]() :
: ![]() g(×) = g(×). (#)
g(×) = g(×). (#)
Поскольку на самом деле детали
сцены, передаваемые распределением цвета j(×), не
представлены на изображении f(×) = f(×)j(×) в той
области поля зрения, в которой яркость f(x)=0, xÎX, будем считать, что ![]() - форма любого изображения f(x)
= f(x)j(x), f(x)>0, xÎX(modm), все такие
изображения изоморфны, а форма всякого изображения g(×),
удовлетворяющего уравнению (#), не сложнее, чем форма f(×).
- форма любого изображения f(x)
= f(x)j(x), f(x)>0, xÎX(modm), все такие
изображения изоморфны, а форма всякого изображения g(×),
удовлетворяющего уравнению (#), не сложнее, чем форма f(×).
Замечание 5. Пусть j1,..., jN![]() - исходный набор цветов,
- исходный набор цветов, ![]() , A1,...,AN
- соответствующее оптимальное разбиение X, найденное в теореие 4 и
, A1,...,AN
- соответствующее оптимальное разбиение X, найденное в теореие 4 и
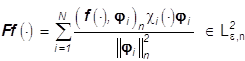 , (34*)
, (34*)
- наилучшее приближение f(×). Тогда в равенстве (24)
если A1,...,AN -
исходное разбиение X в теореме 3. Наоборот, если A1,...,AN -
заданное в теореме 3 разбиение X
и f1,...,fN -
собственные векторы операторов Ф1,...,ФN (23)
соответственно, отвечающие максимальным собственным значениям, то f1,...,fN
![]() и будет выполнено равенство
(24), если в (34*) определить ji как цвет fi в (24), i=1,...,N.
и будет выполнено равенство
(24), если в (34*) определить ji как цвет fi в (24), i=1,...,N.
Проверка этого замечания не представляет затруднений.
В. Случай, когда допускаются небольшие изменения цвета в пределах каждого Ai, i=1,...,N.
Разумеется, условие постоянства
цвета на множествах Ai, i=1,...,N, на практике может выполняться лишь с определенной точностью.
Последнюю можно повысить как путем перехода к более мелкому разбиению ![]() , так и допустив некоторые изменения цвета в пределах каждого Ai, i=1,...,N, например, выбрав вместо
(17) класс изображений
, так и допустив некоторые изменения цвета в пределах каждого Ai, i=1,...,N, например, выбрав вместо
(17) класс изображений
 (17*)
(17*)
в котором ![]() в
(3).
в
(3).
Поскольку в задаче наилучшего
приближения f(×)
изображениями этого класса предстоит найти 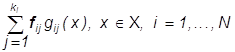 ,
векторы
,
векторы ![]() при любом i=1,...,N,
можно считать ортогональными, определив
при любом i=1,...,N,
можно считать ортогональными, определив
![]() , (*)
, (*)
из условия минимума невязки по ![]() . После этого для каждого i=1,...,N
векторы
. После этого для каждого i=1,...,N
векторы ![]() должны быть определены из
условия
должны быть определены из
условия
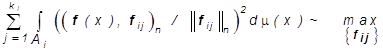 (**)
(**)
при дополнительном условии ортогональности
![]() . Решение этой задачи дается в следующей лемме
. Решение этой задачи дается в следующей лемме
Лемма 5. Пусть ![]() ортогональные собственные
векторы оператора Фi (23), упорядоченные по убыванию
собственных значений:
ортогональные собственные
векторы оператора Фi (23), упорядоченные по убыванию
собственных значений:
![]() .
.
Тогда решение задачи (**) дается равенствами ![]() .
.
Доказательство. Заметим, что,
поскольку Фi - самосопряженный неотрицательно
определенный оператор, его собственные значения неотрицательны, а его
собственные векторы всегда можно выбрать так, чтобы они образовали
ортогональный базис в Rn. Пусть Pi
- ортогонально проецирует в Rn на линейную оболочку ![]() собственных векторов
собственных векторов ![]() и
и
[Pi Фi Pi]
- сужение оператора Pi Фi Pi на ![]() . Тогда левая часть (*)
равна следу оператора [Pi Фi Pi]
. Тогда левая часть (*)
равна следу оператора [Pi Фi Pi]
![]() , где
, где ![]() - j-ое
собственное значение оператора
- j-ое
собственное значение оператора ![]() (см.,
например, [10]). Пусть
(см.,
например, [10]). Пусть ![]() . Тогда
согласно теореме Пуанкаре, [10],
. Тогда
согласно теореме Пуанкаре, [10], ![]() , откуда
следует утверждаемое в лемме. ■
, откуда
следует утверждаемое в лемме. ■
Воспользовавшись выражениями (*) и леммой 5, найдем, что в рассматриваемом случае имеет место утверждение, аналогичное теореме 3.
Теорема 3*. Наилучшее приближение любого изображения f(×) изображениями (17*) имеет вид
![]() ,
,
Где ![]() :
ортогональный проектор на линейную оболочку
:
ортогональный проектор на линейную оболочку ![]() ,
собственных векторов задачи
,
собственных векторов задачи
![]() .
.
Невязка наилучшего приближения равна
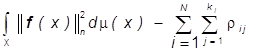 . n
. n
Рассмотрим теперь задачу наилучшего
приближения изображения f(×) изображениями
(17), в которых заданы и фиксированы векторы ![]() ,
и надлежит определить измеримое разбиение
,
и надлежит определить измеримое разбиение ![]() и
функции
и
функции ![]() , как решение задачи
, как решение задачи
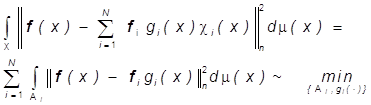 (30)
(30)
При любом разбиении ![]() минимум в (30) по
минимум в (30) по ![]() достигается при
достигается при ![]() , определяемых равенством
(20). В свою очередь, очевидно, что
, определяемых равенством
(20). В свою очередь, очевидно, что
![]() (31)
(31)
где точки ![]() ,
в которых выполняется равенство
,
в которых выполняется равенство ![]() могут
быть произвольно включены в одно из множеств : либо в
могут
быть произвольно включены в одно из множеств : либо в ![]() , либо в
, либо в ![]() . Это соглашение отмечено
звездочкой в (31).
. Это соглашение отмечено
звездочкой в (31).
Таким образом доказана
Теорема 6. Пусть ![]() заданные векторы Rn. Решением задачи (30) является
изображение
заданные векторы Rn. Решением задачи (30) является
изображение
![]() ,
,
где ортогональный проектор ![]() определен равенством
(25), а
определен равенством
(25), а ![]() - индикаторная
функция множества (31), i=1,...,N. Невязка наилучшего приближения
равна
- индикаторная
функция множества (31), i=1,...,N. Невязка наилучшего приближения
равна
![]() . n
. n
Замечание 5. Так как при ![]()
![]() ,
,
то условия (31), определяющие разбиение ![]() , можно записать в виде
, можно записать в виде
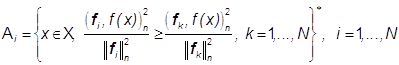 ,
(32)
,
(32)
показывающем, что множество ![]() в (32) инвариантно
относительно любого преобразования изображения
в (32) инвариантно
относительно любого преобразования изображения ![]() ,
не изменяющего его цвет.
,
не изменяющего его цвет.
Теоремы
3 и 6 позволяют сформулировать необходимые и достаточные условия наилучшего
приближения изображения f(×)
изображениями (17), при котором должны быть найдены ![]() и ci0 , i=1,...,N,
такие, что
и ci0 , i=1,...,N,
такие, что


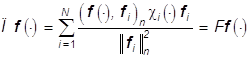 , (24*)
, (24*)