Быстрый поиск

Реферат: Морфологический анализ цветных (спектрозональных) изображений

Следующая рекуррентная процедура, полезная для уточнения приближений, получаемых в теоремах 1,2, в некоторых случаях позволяет решать названную задачу. Пусть - исходные векторы в задаче (14*), - соответствующее оптимальное разбиение (14), F(1)- оператор наилучшего приближения и - невязка. Воспользовавшись теоремой 1, определим для найденного разбиения оптимальные векторы . Согласно выражению (13) 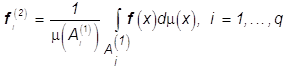, и соответствующий оператор наилучшего приближения П(1) (13) обеспечит не менее точное приближение f(×), чем F(1): . Выберем теперь в теореме 2 , определим соответствующее оптимальное разбиение и построим оператор наилучшего приближения F(2). Тогда . На следующем шаге по разбиению строим и оператор П(3) и т.д.

В заключение этого пункта вернемся к вопросу о построении исчерпывающего -измеримого разбиения X, отвечающего заданной функции . Выберем произвольно попарно различные векторы из f(X) и построим по формуле (15) разбиение Rn . Для каждого q=1,2,... образуем разбиение E(N(q)), множества , j=1,...,N(q), которого образованы всеми попарно различными пересечениями множеств из . Последовательность соответствующих разбиений X , i=1,...,N(q), q=1,2... -измеримы и является продолжением

5.2. Приближение изображениями, цвет которых постоянен на подмножествах разбиения поля зрения X.

Задано разбиение , требуется определить цвет и распределение яркостей наилучшего приближения на каждом Ai,i=1,...,N.

Для практики, как уже было отмечено, большой интерес представляет класс изображений (5), цвет которых не изменяется в пределах некоторых подмножеств поля зрения, и задачи аппроксимации произвольных изображений изображениями такого класса.

Запишем изображение (5) в виде

(17)

где .

Пусть A1,...,AN - заданное разбиение X, - индикаторная функция Ai, i=1,...,N. Рассмотрим задачу наилучшего в приближения изображения изображениями (17), не требуя, чтобы

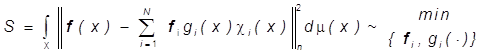(18)

Речь идет о задаче аппроксимации произвольного изображения изображениями, у которых яркость может быть произвольной функцией из , в то время, как цвет должен сохранять постоянное значение на каждом из заданных подмножеств A1,...,AN поля зрения X, (см. Лемму 3).

Так как

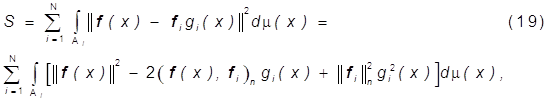
то минимум S (19) по достигается при

, (20)

и равен

(21)

Задача (18) тем самым сведена к задаче

. (22)

В связи с последней рассмотрим самосопряженный неотрицательно определенный оператор

. (23)

Максимум (неотрицательной) квадратичной формы на сфере в Rn, как известно, (см.,например, [11]) достигается на собственном векторе yi оператора Фi, отвечающем максимальному собственному значению >0,

и равен , т.е. . Следовательно, максимум в (22) равен и достигается, например, при

Теорема 3. Пусть A1,...,AN -заданное измеримое разбиение X, причем[9] m(Ai)>0, i=1,...,N. Решением задачи (18) наилучшего приближения изображения изображениями g(×) (17) является изображение

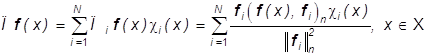(24)

Операторы ,i=1,...,N, и - нелинейные (зависящие от f(×)) проекторы: Пi проецирует в Rn векторы на линейное подпространство , натянутое на собственный вектор оператора Фi (23), отвечающий наибольшему собственному значению ri,

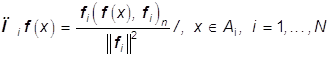; (25)

П проецирует в изображение на минимальное линейное подпространство , содержащее все изображения

Невязка наилучшего приближения

(19*).

Доказательство. Равентство (24) и выражение для Пi следует из (17),(20) и решения задачи на собственные значения для оператора Фi (23). Поскольку Фi самосопряженный неотрицательно определенный оператор, то задача на собственные значения (23) разрешима, все собственные значения Фi неотрицательны и среди них ri - наибольшее.

Для доказательства свойств операторов Пi, i=1,...,N, и П введем обозначения, указывающие на зависимость от f(×):

(26*)

Эти равенства, показывающие, что результат двукратного действия операторов Пi, i=1,...,N, и П (26) не отличается от результатата однократного их действия, позволят считать операторы (26) проекторами.

Пусть fi - cсобственный вектор Фi , отвечающий максимальному собственному значению ri. Чтобы определить следует решить задачу на собственные значения для оператора :

Поскольку rank=1, имеет единственное положительное собственное значение, которое, как нетрудно проверить, равно ri, и ему соответствует единственный собственный вектор fi. Поэтому

Отсюда, в свою очередь, следует равенство (26*) для n

Лемма 4. Для любого изображения решение (24) задачи (18) наилучшего приближения единственно и является элементом .

Доказательство. Достаточно доказать, что единственный (с точностью до положительного множителя) собственный вектор fi оператора (23), отвечающий максимальному собственному значению ri, можно выбрать так, чтобы , поскольку в таком случае будут выполнены импликации:

составляющие содержание леммы. Действительно, если то согласно (23) , поскольку включение означает, что; отсюда и из (25) получим, что ,i=1,...,N, а поэтому и в (24) .

Убедимся в неотрицательности . В ортонормированном базисе e1,...,en, в котором , выходной сигнал i-го детектора в точке (см. замечание 1) задача на собственные значения (23*) имеет вид , p=1,...,n,

где , .

Так как матрица симметрическая и неотрицательно определенная () она имеет n неотрицательных собственных значений, которым соответствуют n ортонормированных собственных векторов , а поскольку матричные элементы , то согласно теореме Фробенуса-Перрона максимальное собственное значение - алгебраически простое (некратное), а соответствующий собственный вектор можно выбирать неотрицательным:

. Следовательно, вектор fi определен с точностью до положительного множителя , . n

Замечание 4.

Если , т.е. если аппроксимируемое изображение на множествах того же разбиения имеет постоянный цвет, то в теореме 3 , .

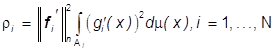Наоборот, если , то

, т.е. определяется выражением (17), в котором .

Итак, пусть в изображении g(×) (17) все векторы f1,.…..,fN попарно не коллинеарны, тюею цвета всех подмножеств A1,...,AN попарно различны. Тогда форма в широком смысле изображения (17) есть множество решений уравнения

,, (27)

где , fi - собственный вектор оператора Фi: , отвечающий максимальному собственному значению ri, i=1,...,N . В данном случае , если и только если выполнено равенство (27).

Оператор П (24), дающий решение задачи наилучшего приближения , естественно отождествить с формой в широком смысле изображения (17).

Заданы векторы цвета j1,..., jq, требуется определить разбиение A1,..., Aq, на множествах которого наилучшее приближение имеет соответственно цвета j1,..., jq и оптимальные распределения яркостей [10].