Курсовая работа: Задача о коммивояжере и ее обобщения

И все приведенные выше алгоритмы являются «жадными».

Следует подчеркнуть, что не каждый «жадный» алгоритм позволяет получить оптимальный результат в целом. Как нередко бывает в жизни, «жадная стратегия» подчас обеспечивает лишь сиюминутную выгоду, в то время как в целом результат может оказаться неблагоприятным.

Существуют задачи, для которых ни один из известных «жадных» алгоритмов не позволяет получить оптимального решения; тем не менее имеются «жадные» алгоритмы, которые с большой вероятностью позволяют получать «хорошие» решения. Нередко вполне удовлетворительным можно считать «почти оптимальное» решение.

3. ГЕНЕТИЧЕСКИЙ АЛГОРИТМ

Генетический алгоритм — это алгоритм, который позволяет найти удовлетворительное решение к аналитически неразрешимым проблемам через последовательный подбор и комбинирование искомых параметров с использованием механизмов, напоминающих биологическую эволюцию. Является разновидностью эволюционных вычислений. Отличительной особенностью генетического алгоритма является акцент на использование оператора «кроссовера», который производит операцию, роль которой аналогична роли скрещивания в живой природе. «Отцом-основателем» генетических алгоритмов считается Джон Холланд, книга которого «Адаптация в естественных и искусственных системах» является основополагающим трудом в этой области исследований.

Задача кодируется таким образом, чтобы её решение могло быть представлено в виде вектора («хромосома»). Случайным образом создаётся некоторое количество начальных векторов («начальная популяция»). Они оцениваются с использованием «функции приспособленности», в результате чего каждому вектору присваивается определённое значение («приспособленность»), которое определяет вероятность выживания организма, представленного данным вектором. После этого с использованием полученных значений приспособленности выбираются вектора (селекция), допущенные к «скрещиванию». К этим векторам применяются «генетические операторы» (в большинстве случаев «скрещивание» - crossover и «мутация» - mutation), создавая таким образом следующее «поколение». Особи следующего поколения также оцениваются, затем производится селекция, применяются генетические операторы и т. Д. Так моделируется «эволюционный процесс», продолжающийся несколько жизненных циклов (поколений), пока не будет выполнен критерий останова алгоритма. Таким критерием может быть: нахождение глобального, либо субоптимального решения; исчерпание числа поколений, отпущенных на эволюцию; исчерпание времени, отпущенного на эволюцию. Генетические алгоритмы служат, главным образом, для поиска решений в очень больших, сложных пространствах поиска.

Таким образом, можно выделить следующие этапы генетического алгоритма:

создание начальной популяции;

вычисление функций полезности для особей популяции (оценивание);

выбор индивидов из текущей популяции (селекция);

скрещивание и\или мутация;

вычисление функций полезности для всех особей;

формирование нового поколения;

если условия совпали, то решение найдено (конец цикла), если нет, то цикл повторяется.

Применяются генетические алгоритмы для решения следующих задач:

оптимизация функций, разнообразные задачи на графах (задача коммивояжера, раскраска, нахождение паросочетаний), настройка и обучение искусственной нейронной сети, задачи компоновки, составление расписаний, игровые стратегии, аппроксимация функций, искусственная жизнь, биоинформатика (свёртывание белков).

4. NP-ПОЛНАЯ ЗАДАЧА

Все эффективные (сокращающие полный перебор) методы решения задачи коммивояжёра — методы эвристические («жадные алгоритмы»). В большинстве эвристических методов находится не самый эффективный маршрут, а приближённое решение. Зачастую востребованы так называемые any-time алгоритмы, то есть постепенно улучшающие некоторое текущее приближенное решение.

Задача коммивояжёра есть NP-полная задача. Часто на ней проводят обкатку новых подходов к эвристическому сокращению полного перебора.

В теории алгоритмов NP-полные задачи — это класс задач, лежащих в классе NP (то есть для которых пока не найдено быстрых алгоритмов решения, но проверка того, является ли данное решение правильным, проходит быстро), к которым сводятся все задачи класса NP.

Назовём языком множество слов над алфавитом Σ. Задачей здесь является определение того, принадлежит данное слово языку или нет. Язык L1 называется сводимым (по Карпу) к языку L2, если существует функция, вычислимая за полиномиальное время, обладающая следующим свойством: f(x) принадлежит L2 тогда и только тогда, когда x принадлежит L1. Язык L2 называется NP-трудным, если любой язык из класса NP сводится к нему. Язык называют NP-полным, если он NP-труден и при этом сам лежит в классе NP. Таким образом, если будет найден алгоритм, решающий хоть одну NP-полную задачу за полиномиальное время, все NP-задачи будут лежать в классе P.

Равенство классов P и NP уже более 30 лет является открытой проблемой. Научное сообщество склоняется к отрицательному решению этого вопроса — в этом случае за полиномиальное время решать NP-полные задачи не удастся.

5. МЕТОД ВЕТВЕЙ И ГРАНИЦ

Существует метод решения задачи коммивояжера, который дает оптимальное решение. Этот метод называется методом ветвей и границ.

Основа этого, ныне широко распространенного метода состоит в построении нижних оценок решения, которые затем используются для отбраковки неконкурентоспособных вариантов.

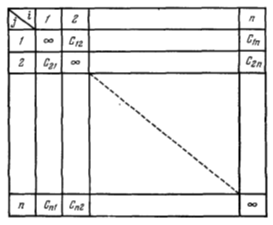
Функция f(xi, xj) принимает конечное число значений сij, которые мы можем представить в виде таблицы (Рисунок 5.1). Предположим, что мы выбрали некоторый путь Ss. Его длина будет равна

 (5.1)

причем сумма (5.1) распространена по i, j так, что каждый из индексов встречается в ней один и только один раз. Величины сij с двумя одинаковыми индексами мы приняли равными ∞.

Так как в каждый из вариантов s входит только один элемент из каждой строки и столбца, то мы можем проделать следующую операцию, которая здесь называется приведением матрицы. Обозначим через hi наименьший элемент из строки номера i и построим новую матрицу С(1) с элементами

 

Матрица С(1) определяет новую задачу коммивояжера, которая, однако, в качестве оптимальной будет иметь ту же последовательность городов. Между величинами ls и ls(1) будет существовать, очевидно, следующая связь:

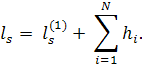
Заметим, что в каждой из строк матрицы С(1) будет теперь, по крайней мере, один нулевой элемент. Далее обозначим через gj наименьший элемент матрицы С(1), лежащий в столбце номера j, и построим новую матрицу С(2) с элементами

 

Величины hi и gj называются константами приведения. Оптимальная последовательность городов для задачи коммивояжера с матрицей С(2) будет, очевидно, такой же, как и для исходной задачи, а длины пути для варианта номера s в обоих задачах будут связаны между собой равенством

                                        (5.2)

где

                        (5. 3)

т. Е. d0 равна сумме констант приведения.

Обозначим через l* решение задачи коммивояжера, т.е.

где минимум берется по всем вариантам s, удовлетворяющим условию (α) Тогда величина d0 будет простейшей нижней оценкой решения:

                                                (5.4)

Будем рассматривать теперь задачу коммивояжера с матрицей С(2) которую мы будем называть приведенной матрицей.

Рассмотрим путь, содержащий непосредственный переход из города номера i в город номера j, тогда для пути s, содержащего этот переход, мы будем иметь, очевидно, следующую нижнюю оценку:

 

Следовательно, для тех переходов, для которых  = 0, мы будем иметь снова оценку (5.4). Естественно ожидать, что кратчайший путь содержит один из таких переходов — примем это соображение в качестве рабочей гипотезы. Рассмотрим один из переходов, для которого  =0, и обозначим через  множество всех тех путей, которые не содержат перехода из i в j.

Так как из города i мы должны куда-то выйти, то множество  содержит один из переходов i→k, где k ≠ j; так как в город номера j мы должны прийти, то множество  содержит переход m→j, где т ≠ i.

Следовательно, некоторый путь ls из множества (ij), содержащий переходы i→k и m→j, будет иметь следующую нижнюю оценку:

 

Обозначим через

 

Тогда очевидно, что для любого ls из множества путей  мы будем иметь оценку

 (5.5)

Мы предполагаем исключить некоторое множество вариантов , поэтому мы заинтересованы выбрать такой переход i → j, для которого оценка (5.5) была бы самой высокой. Другими словами, среди нулевых элементов матрицы С(2) выберем тот, для которого максимально. Это число обозначим через  Таким образом, все множество возможных вариантов мы разбили на два множества I1 и I2. Для путей из множества I1, мы имеем оценку (5.4). Для путей из множества I2 оценка будет следующей:

 (5.6)

Рассмотрим теперь множество I1 и матрицу С(2). Так как все пути, принадлежащие этому множеству, содержат переход i → j , то для его исследования нам достаточно рассмотреть задачу коммивояжера, в которой города номеров i и j совпадают. Размерность этой задачи будет уже равна N – 1, а ее матрица получится из матрицы С(2) вычеркиванием столбца номера j и строки но мера i.

Поскольку i → j невозможен, то элемент  принимаем равным бесконечности.

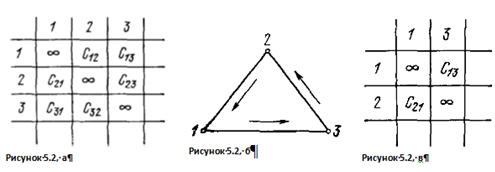
Рассмотрим случай N=3 (Рисунок 5.2, а), и предположим, что мы рассматриваем тот вариант, который содержит переход 3 → 2. Тогда задача коммивояжера после вычеркивания третьей строки и второго столбца вырождается в тривиальную. Ее матрица изображена на рисунке 5.2, в. В этом случае мы имеем единственный путь, и его длина будет, очевидно, равна сумме

 

Итак, если в результате вычеркивания строки номера i и столбца номера j мы получим матрицу второго порядка, то задачу можно считать решенной.

Пусть теперь N >3. После вычеркивания мы получим матрицу порядок

 

N -1 > 2.

С этой матрицей (N — 1)-го порядка совершим процеурру приведения. Матрицу, которую таким образом получим, обозначим через С(3), а через d(1) – сумму ее констант приведения. Тогда для ls  I1, мы будем иметь оценку

                             (5.7)

На этом первый шаг алгоритма закончен. В результате одного шага мы разбили множество всех возможных вариантов на два множества I1 и I2 и для путей, принадлежащих этим множествам, мы получили оценки (5.7) и (5.6) (Рисунок 5.3)

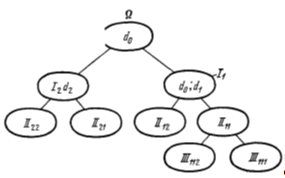
Рис.5.3

Введем понятие стандартной операции, которую мы будем обозначать символом  Этим термином мы назовем процедуру разбиения произвольного множества вариантов Ω с приведенной матрицей N – п-го порядка С(n + 2) и оценкой dω на два множества. Одно из этих множеств состоит из всех тех путей, которые содержат переход из города номер s в город номер l и имеют нижнюю оценку d . Другое множество состоит из всех путей, не содержащих этого перехода и имеющих в качестве нижней оценки число dk. Стандартную операцию можно представить в форме следующей блок-схемы (см. Рисунок 5.4).

задача коммивояжер решение алгоритм обобщение

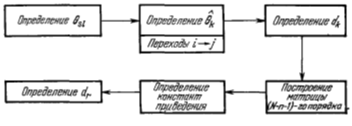
Рисунок 5.4

Итак, первый шаг метода ветвей и границ состоит в проведении стандартной операции над исходным множеством Ω. На следующем шаге мы продолжаем развивать дерево возможных вариантов. Сначала мы сравниваем две оценки d1 и d2 и для последующего анализа выбираем то из множеств I1 или I2, для которого соответствующая оценка меньше.

Предположим, что

d1 < d2;

тогда над множеством I1 с матрицей С(3) мы совершим стандартную операцию. В результате мы разобьем множество возможных вариантов I1 на два подмножества II11 и II12, первое из которых содержит некоторый переход i1 → j1 а другое содержит все пути, не имеющие непосредственною перехода из города i1 в город j1. Еще раз повторим рассмотренную выше процедуру: для каждого из нулевых элементов матрицы С(3) построим число

 

Определим значение

 

и элемент матрицы С(3), для которого достигается это значение. Если ls  II12, то

                           (5.8)

Затем в матрице С(3) вычеркиваем строку номера i1 и столбец номера j1, полагаем  и над полученной матрицей совершаем операцию приведения. В результате мы найдем новые константы приведения. Их сумму обозначим через d(II) и в заключение находим оценку d11 для элементов множества II11.

Если ls  II11, то

                          (5.9)

На этом второй шаг алгоритма ветвей и границ закончен. Мы разбили множество вариантов I1 на два множества, II11 и II12, и для элементов этих множеств получили нижние оценки (5.9) и (5.8), соответственно.

Теперь мы должны сравнить оценку (5.9) с оценкой (5.6) для элементов множества I2, которое мы исключили из рассмотрения на предыдущем шаге. Если окажется, что d2 > d11,

то мы переходим к третьему шагу, который состоит в применении стандартной операции к множествуII11. (Если размерность матрицы при этом равна двум, то, как мы видели выше, процесс заканчивается.)

Если окажется, что d11 > d2, то множеством вариантов с оптимальной нижней оценкой будет множество I2. Другими словами, теперь будем предполагать, что наиболее короткий путь содержится среди элементов множества I2 — множества всех вариантов, не содержащих перехода i → j. Следовательно, матрица, характеризующая это множество, получается из матрицы С(2) заменой величины  на ∞. Над этим множеством мы производим стандартную операцию и разбиваем его на два множества II21 и II22 с оценками d21 и d22, соответственно. Одновременно мы выделяем переход k→l, который содержит все варианты множества II21. Затем мы снова сравниваем все оценки d11, d12, d21 и d22 и выбираем то из множеств, для которого оценка будет наименьшей. Над выбранным множеством совершаем стандартную операцию и т. Д. Так мы продолжаем до тех пор, пока очередная матрица не будет иметь порядок (2x2). В этом случае, как мы видели, расчет заканчивается — мы получаем задачу коммивояжера для двух городов (Рисунок 5.5), и длина единственного маршрута будет

Итак, мы получили некоторую цепочку (ветвь) переходов, длину которой мы вычислили. Сам порядок построения этой цепочки показывает, что ее длина — наименьшая среди всех ветвей дерева, изображенного на рисунке 5.3.

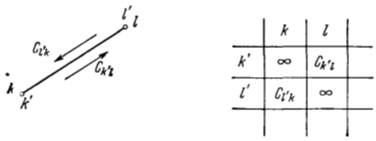
Рисунок 5.5

6. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ЗАДАЧИ КОММИВОЯЖЕРА

Задача коммивояжера имеет ряд практических применений. Как следует из самого названия задачи, ее можно использовать для составления маршрута человека, который должен посетить ряд пунктов и, в конце концов, вернуться в исходный пункт. Например, задача коммивояжера использовалась для составления маршрутов лиц, занимающихся выемкой монет из таксофонов. В этом случае вершинами являются места установки таксофонов и "базовый пункт". Стоимостью каждого ребра (отрезка маршрута) является время в пути между двумя точками (вершинами) на маршруте.

Задача о производстве красок. Имеется производственная линия для производства n красок разного цвета; обозначим эти краски номерами 1,2… n. Всю производственную линию будем считать одним процессором.. Будем считать также, что единовременно процессор производит только одну краску, поэтому краски нужно производить в некотором порядке. Поскольку производство циклическое, то краски надо производить в циклическом порядке (j1,j2,..,jn,j1). После окончания производства краски i и перед началом производства краски j надо отмыть оборудование от краски i. Для этого требуется время C[i,j]. Очевидно, что C[i,j] зависит как от i, так и от j, и что, вообще говоря,C[i,j] ≠ C[j,i]. При некотором выбранном порядке придется на цикл производства красок потратить время, где tk - чистое время производства k-ой краски (не считая переналадок). Однако вторая сумма в правой части постоянна, поэтому полное время на цикл производства минимизируется вместе с общим временем на переналадку.

Таким образом, задачи коммивояжера и задача о минимизации времени переналадки – это просто одна задача, только варианты ее описаны разными словами.

Задача о дыропробивном прессе. Дыропробивной пресс производит большое число одинаковых панелей – металлических листов, в которых последовательно по одному пробиваются отверстия разной формы и величины. Схематически пресс можно представить в виде стола, двигающегося независимо по координатам x, y, и вращающегося над столом диска, по периметру которого расположены дыропробивные инструменты разной формы и величины. Каждый инструмент присутствует в одном экземпляре. Диск может вращаться одинаково в двух направлениях (координата вращения z). Имеется собственно пресс, который надавливает на подвешенный под него инструмент тогда, когда под инструмент подведена нужная точка листа. Операция пробивки j-того отверстия характеризуется четверкой чисел (xj,yj,zj,tj),, где xj,yj- координаты нужного положения стола, zj - координата нужного положения диска и tj -время пробивки j-того отверстия.

Производство панелей носит циклический характер: в начале и конце обработки каждого листа стол должен находиться в положениях (x0, y0) диск положении z0 причем в этом положении отверстие не пробивается. Это начальное состояние системы можно считать пробивкой фиктивного нулевого отверстия. С параметрами (x0,y0,z0,0). Чтобы пробить j-тое отверстие непосредственно после i-того необходимо произвести следующие действия:

1. Переместить стол по оси x из положения xi в положение xj, затрачивая при этом время t(x)(|xi-xj|)=ti,j(x);

2. Проделать то же самое по оси y, затратив время ti,j(y);

3. Повернуть головку по кратчайшей из двух дуг из положения zi в положение zj, затратив время ti,j(z);

4. Пробить j-тое отверстие, затратив время tj.

Конкретный вид функций t(x), t(y), t(z) зависит от механических свойств пресса и достаточно громоздок. Явно выписывать эти функции нет необходимости. Действия 1-3 (переналадка с i-того отверстия j-тое) происходит одновременно, и пробивка происходит немедленно после завершения самого длительного из этих действий. Поэтому С[i,j] = max(t(x), t(y), t(z)). Теперь, как и в предыдущем случае, задача составления оптимальной программы для дыропробивного пресса сводится к задачи коммивояжера (здесь - симметричной).

Еще одним применением задачи коммивояжера является задача обхода доски шахматным конем: надо найти последовательность ходов, которые позволят коню обойти все поля шахматной доски, попадая на каждое поле лишь один раз, и вернуться, в конце концов, на исходное поле. В этом случае роль вершин графа выполняют поля шахматной доски. Предполагается также, что ребра между двумя полями, которые являются "составными частями" хода коня, имеют нулевой вес; все остальные ребра имеют вес, равный бесконечности. Оптимальный маршрут имеет нулевой вес и должен быть маршрутом коня. Читатель, возможно, удивится, узнав, что поиск маршрутов коня с помощью хороших эвристических алгоритмов для задачи коммивояжера вообще не составляет проблемы, в то время как поиск "вручную" является весьма непростой задачей.

ЗАКЛЮЧЕНИЕ

Задача коммивояжера является частичным случаем гамильтоновой задачи о путешественнике. Суть задачи коммивояжера состоит в нахождении суммарной минимальной характеристики (расстояния, стоимости проезда и т.д.), при этом коммивояжер должен пройти все n городов по одному разу, вернувшись в тот город, с которого начал.

Существуют несколько методов решения задачи коммивояжера: метод полного перебора, «жадные» методы (Крускала, Прима, и т.п.), генетические алгоритмы и еще множество их обобщений. Однако только метод ветвей и границ дает нам в итоге самое оптимальное решение.

В основе метода ветвей и границ лежит следующая идея если нижняя граница для подобласти A дерева поиска больше, чем верхняя граница какой-либо ранее просмотренной подобласти B, то A может быть исключена из дальнейшего рассмотрения (правило отсева).

Задача о коммивояжере имеет множество обобщений и методы её решения в различных проявлениях используются на практике.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1  Моисеев Н.Н. Методы оптимизации: Моисеев Н.Н., Иванилова Ю.П., Столярова Е.М.-М., 1978, 352 с;

2  Черноусько Ф.Л. Вариационные задачи механики и управления: Численные методы/ Черноусько Ф.Л., Баничук Н.В.-М.,1973;

3  http://dic.academic.ru/;

4  http://www.lobanov-logist.ru/index.php?newsid=470;

5  http://swsys.ru/index.php?page=article&id=827;

6  http://e-maxx.ru/algo/mst_prim;

7  http://www.dissercat.com/content/nekotorye-zadachi-marshrutizatsii-i-raspredeleniya-zadanii-metod-dinamicheskogo-programmirov;

8  www.vecon.ru.