Курсовая работа: Транспортная задача линейного программирования

Выбор в качестве х минимального среди чисел, стоящих в отрицательных вершинах цикла, обеспечивает допустимость нового базиса.

Если минимальное значение среди базисных неизвестных, стоящих в отрицательных вершинах цикла, принимается не в одной отрицательной вершине, то свободной оставляют только одну из них, а в других клетках с тем же минимальным значением пишут нули. В этом случае новое базисное решение будет вырожденным.

Может случиться, что и само минимальное значение среди чисел в отрицательных клетках равно нулю. Тогда преобразование таб­лицы перевозок сведется к перестановке этого нуля в свободную клетку. Значения всех неизвестных при этом остаются неизменными, но решения считаются различными, так как различны базисы. Оба решения вырождены.

Описанное выше преобразование таблицы перевозок, в результате которого преобразуется базис, называется пересчетом по циклу.

Заметим, что неизвестные, не входящие в цикл, этим преобразованием не затрагиваются, их значения остаются неизменными и каж­дое из них остается либо в группе базисных, либо в группе свобод­ных неизвестных, как и до пересчета.

Выясним теперь, как пересчет по циклу влияет на общий объем затрат на перевозки и при каком условии эти затраты становятся меньше.

Пусть  – некоторое свободное неизвестное, для которого мы построили цикл и осуществили пересчет по циклу с некоторым числом . Если вершине цикла, находящейся в  строке и  столбце таблицы перевозок, приписан знак “+”, то значение неизвестного , находящегося в этой вершине, увеличивается на , что в свою очередь вызывает увеличение затрат на . где  – тариф, соответствующий этой клетке; если же указанной вершине приписан знак “–”, то значение неизвестного  уменьшается на , что вызывает уменьшение затрат на .

Сложим тарифы, соответствующие положительным вершинам цикла, и вычтем из этой суммы сумму тарифов, соответствующих отрицательным вершинам цикла; полученную разность  назовем алгебраической суммой тарифов для данного свободного неизвестного . Подсчет алгебраической суммы тарифов можно истолковать и так: припишем тарифам те же знаки, которые приписаны соответствующим вершинам цикла, тогда алгебраическая сумма тарифов равна сумме таких тарифов со знаком (“относительных тарифов”).

Теперь, очевидно, мы можем, заключить, что в целом при пере­счете но циклу, соответствующему свободному неизвестному  общий объем затрат на перевозки изменится на произведение алгеб­раической суммы тарифов на , т. е. на величину . Следовательно, если алгебраическая сумма тарифов для некоторого свобод­ного неизвестного  отрицательна , то пересчет по циклу, соответствующему этому неизвестному, приводит к уменьшению общей суммы затрат на реализацию плана перевозок. Если же алгебраическая сумма тарифов положительна , то пересчет по соответствующему циклу приведет к увеличению общей суммы затрат. И, наконец, если алгебраическая сумма тарифов равна нулю , то пересчет по соответствующему циклу не изменит общую сумму затрат (два различных базисных плана требуют одинаковых затрат на их реализацию).

Так, например, для цикла  в рассмотренной задаче алгебраическая сумма тарифов

.

Значит, пересчет по этому циклу снижает расходы. И действитель­но, осуществив такой пересчет, мы получаем план, по которому объем перевозок в тонно-километрах составляет

тогда как по исходному плану он составил . Имеем снижение объема перевозок на 1200 тонно-километров, что и следовало ожидать, так как алгебраическая сумма тарифов в дан­ном случае равна –15, а пересчет по циклу осуществляется с помощью числа  (изменение затрат равно ).

Вычисление алгебраической суммы тарифов для каждого из сво­бодных неизвестных можно производить без построения соответ­ствующего цикла, пользуясь, так называемыми, потенциалами. При­пишем каждой базе , некоторое число  и каждому потребителю  некоторое число :

,

так что

(4.1)

,

где  – тарифы, соответствующие клеткам, заполненным базис­ными неизвестными. Эти числа  и  называются потенциалами соответствующих баз и потребителей.

Зная потенциалы, легко вычислить алгебраическую сумму тари­фов. Действительно, если в алгебраической сумме тарифов по циклу, соответствующему свободному неизвестному , заменить тарифы базисных клеток их выражениями через потенциалы по формулам (4.1), то, в силу чередования знаков при вершинах цикла, все потенциалы, кроме  и  сократятся, и мы получим:

.

Так, например, для цикла  в рассмотренной выше задаче имеем

.

Для базисных клеток сумма потенциалов строки и столбца, в которых находится эта клетка, равна тарифу, соответствующему этой клетке; если же клетка для неизвестного  свободная, то сумму потенциалов

(4.2)

называют косвенным тарифом этой клетки. Следовательно, алгеб­раическая сумма тарифов для свободной клетки  равна разности ее настоящего (“истинного”) и косвенного тарифов:

(4.3)

Из (4.3) следует, что если косвенный тариф для данной свобод­ной клетки больше её истинного тарифа, то алгебраическая сумма тарифов по циклу, соответствующему этой клетке, будет отрица­тельна; если же косвенный тариф меньше истинного, то алгебраи­ческая сумма тарифов положительна, и, наконец, если косвенный тариф равен истинному, то алгебраическая сумма тарифов равна нулю.

Потенциалы можно найти из системы равенств (4.1), рассматри­вая их как систему  уравнений с  неизвестными. Так как неизвестных здесь на единицу больше, чем уравнений, то, по крайней мере, один из потенциалов мы можем выбрать произвольно, положив, например, ; тогда остальные потенциалы легко опре­деляются из уравнений (4.1).

Например, для плана, полученного по диагональному методу в рассмотренной выше задаче, имеем

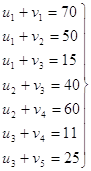
Система содержит семь уравнений с восемью неизвестными. Выбирая произвольно значение , находим последовательно из пер­вых трех уравнений значения , , , затем из четвертого уравнения – , из пятого уравнения – , из шестого уравнения  и, наконец, из седь­мого уравнения – .

Положив, например, , получаем значения потенциалов:

 

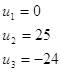
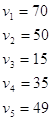
Найдем теперь косвенные тарифы для свободных клеток и сравним их с истинными тарифами:

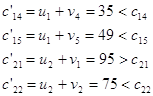
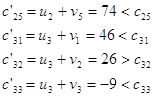
Для клеток с неизвестными  и  косвенные тарифы больше истинных. Следовательно, для них мы будем иметь отрицательные алгебраические суммы тарифов:

Значение  мы уже имели раньше, вычисляя алгебраиче­скую сумму тарифов для этой клетки непосредственно по циклу.

Замечание 1. Подсчитывая косвенные тарифы как суммы соответ­ствующих потенциалов, полезно не пропускать и клетки с базисны­ми неизвестными (заполненные клетки). Для этих клеток сумма потенциалов равна истинному тарифу; последнее может служить проверкой правильности найденных значении потенциалов.

Замечание 2. Можно показать, что если сумму всех затрат по данному плану перевозок выразить через свободные неизвестные [для этого надо исключить базисные неизвестные из выражения для S, см. формулу (2.4)], то коэффициент при каждом из таких неизвестных будет равен алгебраической сумме тарифов по циклу, соответствующему ей в таблице перевозок. Это еще раз подтверждает, что пересчет по циклам является специфической формой применения симплекс-метода к решению транспортной задачи.

Критерий оптимальности базисного решения транспортной задачи. Методы отыскания оптимального решения.

Из сказанного в предыдущем пункте вытекает следующий кри­терий оптимальности базисного решения транспортной задачи: если для некоторого базисного плана перевозок алгебраические суммы тарифов по циклам для всех свободных клеток неотрицательны, то этот план оптимальный.

Отсюда вытекает способ отыскания оптимального решения транспортной задачи, состоящий в том, что, имея некоторое базис­ное решение, вычисляют алгебраические суммы тарифов для всех свободных клеток. Если критерий оптимальности выполнен, то дан­ное решение является оптимальным; если же имеются клетки с отрицательными алгебраическими суммами тарифов, то переходят к новому базису, производя пересчет по циклу, соответствующему одной из таких клеток. Полученное таким образом новое базисное решение будет лучше исходного – затраты на его реализацию будут меньшими. Для нового решения также проверяют выполнимость критерия оптимальности и в случае необходимости снова совершают пересчет по циклу для одной из клеток с отрицательной алгебраиче­ской суммой тарифов и т. д.

Через конечное число шагов приходят к искомому оптимальному базисному решению.

В случае если алгебраические суммы тарифов для всех свобод­ных клеток положительны, мы имеем единственное оптимальное решение; если же алгебраические суммы тарифов для всех свобод­ных клеток неотрицательны, но среди них имеются алгебраические суммы тарифов, равные нулю, то оптимальное решение не единствен­ное: при пересчете по циклу для клетки с нулевой алгебраической суммой тарифов мы получим оптимальное же решение, но от­личное от исходного (затраты по обоим планам будут одина­ковыми).

В зависимости от методов подсчета алгебраических сумм тари­фов для свободных клеток различают два метода отыскания опти­мального решения транспортной задачи:

Распределительный метод. При этом методе для каждой пустой клетки строят цикл и для каждого цикла непосредственно вычисляют алгебраическую сумму тарифов.

Метод потенциалов. При этом методе предварительно находят потенциалы баз и потребителей, а затем вычисляют для каждой пустой клетки алгебраическую сумму тарифов с помощью потен­циалов.

Преимущества метода потенциалов по сравнению с распредели­тельным методом состоят в том, что отпадает необходимость построения циклов для каждой из пустых клеток и упрощается вычисление алгебраических сумм тарифов. Цикл строится только один – тот, по которому производится пересчет.

Применяя метод потенциалов, можно говорить не о знаке алгебраических сумм тарифов, а о сравнении косвенных тарифов с истинными. Требование неотрицательности алгебраических сумм тарифов заменяется условием, что косвенные тарифы не превосхо­дят истинных.

Следует иметь в виду, что потенциалы (так же как и циклы) для каждого нового базисного плана определяются заново.

Выше рассматривалась закрытая модель транспортной задачи, с правильным балансом, когда выполняется условие (1.3). В случае выполнения (1.4) (открытая модель) баланс транспортной задачи может нарушаться в 2-ух направлениях:

1. Сумма запасов в пунктах отправления превышает сумму поданных заявок (транспортная задача с избытком запасов):

 å аi > å bj ( где i=1,...,m ; j=1,...,n );

2. Сумма поданных заявок превышает наличные запасы (транспортная задача с избытком заявок): 

 å аi < å bj ( где i=1,...,m ; j=1,...,n );

Рассмотрим последовательно эти два случая:

Транспортная задача с избытком запасов.

Сведем её к ранее рассмотренной транспортной задаче с правильным балансом. Для этого, сверх имеющихся n пунктов назначения В1, B2, ... , Bn, введём ещё один, фиктивный, пункт назначения Bn+1, которому припишем фиктивную заявку, равную избытку запасов над заявками 

 bn+1 = å аi - å bj ( где i=1,...,m ; j=1,...,n ) ,

а стоимость перевозок из всех пунктов отправления в фиктивный пункт назначения bn+1 будем считать равной нулю. Введением фиктивного пункта назначения B n+1 с его заявкой b n+1 мы сравняли баланс транспортной задачи, и теперь ее можно решать, как обычную транспортную задачу с правильным балансом.

Транспортная задача с избытком заявок.

Эту задачу можно свести к обычной транспортной задаче с правильным балансом, если ввести фиктивный пункт отправления Am+1 с запасом am+1 равным недостающему запасу, и стоимость перевозок из фиктивного пункта отправления во все пункты назначения принять равной нулю.

Задача, двойственная к транспортной.

Страницы: 1, 2, 3, 4, 5, 6, 7