Курсовая работа: Теорема Силова

(Mx)φ=Nx для xÎH.

Отображение φ однозначно, так как из Mx=My следует Nx=Ny. Отображение φ переводит разные элементы в разные , так как из Nx=Ny следует Mx=My. Наконец, φ – отображение на, так как каждое Nx имеет прообраз Mx. ■

Пусть M – подмножество, H – подгруппа группы G. Мы назвали нормализатором M в H совокупность тех элементов из H, которые перестановочны с множеством M в целом. Можно рассмотреть также множество тех элементов из H, которые перестановочны с M поэлементно, то есть

CH(M)=.

Это множество называется централизатором множества M в подгруппе H. Если M состоит из одного элемента, то, конечно, его нормализатор и централизатор в H совпадают. Если не указано, в какой подгруппе H берется централизатор, то это означает, что он берется во всей группе G.

Централизатор всей группы G называется её центром и обозначается Z(G),

Z(G)=.

Очевидно, что группа тогда и только тогда абелева, если она совпадает со своим центром. Ясно, что единица е всегда лежит в центре. Если других центральных элементов группа не содержит, то она называется группа с тривиальным центром. Заметим ещё, что любая подгруппа центра нормальна в группе.

Теорема 1.4.2. Пусть , где p – простое число. Тогда центр Z(G) группы G нетривиальный, то есть содержит неединичные элементы.

Доказательство. Ранее было показано (см.  3), что любая группа G разбивается на не пересекающие классы сопряженных элементов. Среди классов будут одноэлементные образованные элементами центра, причем их число неравно нулю, так как единица е группы G образуют одноэлементный класс.

Пусть число элементов центра равно t. Все элементы, не принадлежащие центру Z(G), порождают классы сопряженных элементов. Обозначим , классы сопряженных элементов содержащие более одного элемента. Число элементов в каждом таком классе есть индекс централизатора любого элемента класса (по теореме 1.4.1. учитывая, что нормализатор и централизатора одного элемента совпадают):

 .

Следовательно, по теореме Лагранжа , где .

Тогда , из этого равенства следует, что t делиться на p и так как , то  таким образом централизатор Z(G) группы G нетривиален. ■

Далее докажем одно несложное утверждение которое понадобиться в дальнейшем.

Предложение 1.4.3. Фактор группа некоммутативной группы G по её центру Z(G) не может быть циклической.

Доказательство (от противного). Действительно, если G/Z(G) циклическая, то в смежном классе по Z являющимися образующим элементом этой циклической группы. Выберем некоторый элемент а. Подгруппа, порождающая этим элементом вместе с элементами из Z(G) совпадает со всей группой G. Из перестановочности между собой названных элементов следует коммутативность самой группы G –противоречие с условием. ■

Из доказанной выше теоремы 1.4.2 и предложения 1.4.3 вытекает следующее утверждение.

Теорема 1.4.4. Любая группа G порядка p2, где p – простое число, коммутативна.

Доказательство (от противного). Пусть G – не коммутативная группа, так как G является p-группой (конечная группа P является p-группой, если ), то её центр не единичен, то есть . Рассмотрим G/Z(G). Порядок G/Z(G) равен p по теореме Лагранжа, следовательно, G/Z(G) – циклическая (см. следствие 2 теоремы Лагранжа) – противоречие с предложением 1.4.3. Таким образом G – коммутативна. ■

п.2. Рассмотрим конструкцию, позволяющую по заданным группам строить новые группы. Одна из самых простых, но важных конструкций состоит в следующем.

Пусть A, B – группы, легко проверить, что множество  всех упорядоченных пар (a, b) где ,  с бинарной операцией  является группой. Она называется прямым произведением (внешним) групп A и B. При аддитивной записи групп, естественно говорить о прямой сумме .

Теорема 1.4.5. Пусть G – группа с нормальными подгруппами A и B. Если  и AB=G, то .

Доказательство. Из равенства AB=G следует, что любой элемент  записывается в виде g=ab, где  . Пусть ещё G=a1b1,  . Тогда ,  и . Следовательно,   и мы пришли к выводу, что запись  однозначна.

Далее, так как  то коммутатор ; так как , то , то есть, получаем  и, стало быть .

Определим теперь отображение φ из . Полагая  для любого . Проверим закон сохранения операции. Согласно выше сказанному:

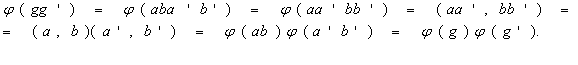
Это отображение является сюрьективным, ибо G=AB. Более того, отображение φ является взаимно однозначным так как если ab=a1b1 при ,  то, как это мы показали, выше a1=a, b1=b и, следовательно,  таким образом φ – удовлетворяет всем свойствам изоморфного отображения групп. ■

Группу G, удовлетворяющую условиям теоремы 1.4.5 принято называть (внутренним) прямым произведением своих подгрупп A, B. Отличие от внешнего прямого произведения состоит в том, что G содержит в качестве прямых множителей сами группы A, B, а не просто их изоморфные копии , .

Последние определение прямого произведения (внутреннего). Можно заменить следующим ему эквивалентным. Группа G есть прямое произведение своих подгрупп , если

1)  Элементы из любых двух подгрупп Hi и Hj, , перестановочны между собой.

2)  Всякий элемент g и G однозначно записываются в виде произведения

где ,                                         

1.5 Теоремы о гомоморфизмах

Пусть G – группа и P – другая группа. Пусть каждому элементу aÎG сопоставлен некоторый элемент из S, то есть, дано отображение G и S. Отображение φ называется гомоморфным или гомоморфизмом G в S, если произведение элементов из G соответствует произведение их образов, то есть

φ(a1a2)=φ(a1)φ(a2), где φ(a) – образ aÎG при отображение φ.

Предложение 1.5.1. Гомоморфным образом φ(G) группы G является группой. Образом единицы группы G является единица образа, и взаимно обратным элементом G соответствуют взаимно обратные образы.

Доказательство. φ(ab)=φ(a)φ(b) означает, что произведение двух элементов из φ(G)Îφ(G). Ассоциативность следует из ассоциативности в G и S. Равенство φ(a)=φ(1a)=φ(1)φ(a) показывает, что φ(1) есть левая единица для φ(G). А φ(а–1)φ(а)=φ(а–1а)=φ(1) показывает, что φ(а–1) есть левый обратный элемент для φ(а) в φ(G). Это достаточно для заключения, что φ(G) есть группа (так как φ(а)=φ(а 1)=φ(а)φ(1) и φ(а)φ(а–1)=φ(аа–1)=φ(1)). ■

Гомоморфизм G в S, при котором различным элементам из G сопоставляется различные элементы в S.

Всякое изоморфное отображение группы G на себя называется автоморфизмом. Если в группе G выбран некоторый элемент а, то отображение, переводящее всякий элемент х этой группы в элемент

а–1ха, то есть трансформирование всей группы элементов а, будет автоморфизмом группы G. Действительно, из а–1ха=а–1ya следует x=y, то есть отображение взаимно однозначно. Равенство х=а–1(аха–1)а

показывает, что при этом отображении всякий элемент группы будет образом некоторого элемента. Из соотношения a–1xa· a–1ya=a–1(xy)a

следует изоморфизм рассматриваемого отображения. Такой автоморфизм группы G называется её внутренним автоморфизмом.

Пусть φ – гомоморфное отображение группы G на группу S. Множество всех элементов из G, имеющих один и тот же образ хÎS, называется полным прообразом элемента х и обозначается φ–1(х). Полный прообраз единицы группы S называется ядром гомоморфизма.

Предложение 1.5.2. Ядро гомоморфизма φ группы G на группу S является нормальной подгруппой группы G.

Доказательство. Введем обозначение H для ядра. Если aÎH, то

a–1ÎH, ибо

φ(a–1)=(φ(a))–1=1. Если aÎH и bÎH, то abÎH, ибо φ(ab)=φ(a)φ(b)=1·1=1. Наконец, если aÎH и cÎG, то c–1acÎH, ибо

φ(c–1ac)=φ(c)–1φ(a)φ(c)=φ(c)–11φ(c)=1. ■

Предложение 1.5.3. В условиях предложения 1.5.2. полные прообразы элементов из S является классами смежности по ядру гомоморфизма.

Доказательство. Если a и b принадлежат одному классу смежности по H, то b=za при zÎH, тогда φ(b)=φ(z)·φ(a)=1·φ(a)=φ(a). Обратно, если φ(a)=φ(b), то φ(ab-1)=1, так что ab-1ÎH, aÎHb и bÎHb. ■

Теорема 1.5.4. (первая теорема о гомоморфизме) Гомоморфный образ группы изоморфен её факторгруппе по ядру гомоморфизма.

Доказательство. Между образами при гомоморфизме и элементами факторгруппы имеется взаимно однозначное соответствие, в силу предложения 1.5.3. Оно сохраняется при умножении, ибо

φ((Ha)·(Hb))=φ(Ha)·φ(Hb).

Остается доказать любая ли нормальная подгруппа может быть принята за ядро гомоморфизма. Ответ положительный, так как отображение группы G на факторгруппу G/H по нормальной подгруппе H, заключающиеся в том, что каждому элементу группы G сопоставляется содержащий его класс смежности, есть гомоморфизм, и его ядро совпадает с H (это следует из определения умножение классов смежности как элементов факторгруппы). ■

Предложение 1.5.5. H и K подгруппы группы G и , тогда  является подгруппой группы ,  и .

Доказательство. Пусть  причем  тогда рассмотрим (hk)–1= k-1h-1 (по одному из основных свойств группы):

, причем , так как  поэтому,  таким образом, для каждого элемента  существует обратный .

Страницы: 1, 2, 3, 4, 5, 6