Курсовая работа: Применение метода ветвей и границ для задач календарного планирования

D(0) = max {dA(0), dB (0), dC (0)}  (25), где       

; ;          (26).

2) Первый шаг. Образование  множеств  G1(1), G2(1) , …, Gn(1), подмножество Gk определяется всеми последовательностями с началом ik(k, ...,n).

Вычисление оценок. Оценку для последовательности sk определяют из соотношения (24), т. е. D(sk) = max {dA(sk), dB (sk), dC (sk)}; k = 1,…,n.  (27).

Выбор варианта для продолжения. Из всех подпоследовательностей, построенных на предыдущем шаге, выбирают наиболее перспективную последовательность sk с наименьшей оценкой, т. е. D(sk(1))=min D(sj(1)).  (28)

Ветвление. Выбрав наиболее перспективный вариант последовательности sk(1), развивают его построением всех возможных подпоследовательностей длиной 2 с началом sk(1) вида  sk+1(2)= (sk(1), j), где j не входит в sk.

Вычисление оценок производят в соответствии с соотношениями (21), (22), (23).

3) k-й шаг. Допустим, что уже проведено k шагов, в результате чего построены варианты s1(k), s2(k) ,…,sk(k), а именно подпоследовательности длиной k.

Выбираем самый перспективный вариант sS(k) такой, что

D(ss(k))=min D(sj(k)).

Множество Gs(k) разбиваем на (n — k) подмножеств, каждое из которых образуется добавлением к последовательности ss(k) некоторого элемента ik+1 такого, что ik+1.

Оценка  определяется в соответствии с соотношениями (21) — (24).

В результате строим дерево вариантов следующего вида: вершина О отвечает s = 0, вершины первого уровня G1(1), G2(1)..., Gn(1) соответствуют последовательностям длиной 1, т. е. s1(1) = 1, s2(1) = 2,..., sn(1) = п и т. д. Каждая конечная вершина отвечает последовательности максимальной длины n.

Признак оптимальности. Если sv(n) отвечает конечной вершине дерева, причем оценка  наименьшая из оценок всех вершин, то sv(n) — искомый вариант.

 

§2. Пример использования метода ветвей и границ в задаче трех станков

Для того, чтобы придать формальной схеме прикладное значение, рассмотрим конкретный пример задачи трех станков.

Решим задачу трех станков, условия которой приведены в табл. 1:

Таблица 1

Длительность операций	Деталь
	1	2	3	4	5
ai bi ci	2 3 4	5 2 4	1 1 2	3 4 2	3 5 2

1) Нулевой шаг. s = 0.

dA(s = 0) = A(0) +  +  = 0 + 14 + 3 = 17;

dB(s = 0) = В(0) +  +  = 0 + 15 + 2 = 17;

dC(s = 0) = С(0) + =14 .

Тогда

∆ (s = 0) = max {17, 17,14} = 17.

2) Первый шаг. Конструируем все возможные последовательности длиной 1

s1(1) = 1; s2(1) = 2;  s3(1) = 3;  s4(1) = 4;  s5(1) = 5.

Находим:

dA(1) = A1 +  +  = 14 + 3 = 17;

dB(1) = В1 +  +  = 5 + 12 + 2 = 19;

dC(1) = С1 + = 9 + 10 = 19 .

Откуда ∆ (1) = max {17, 19, 19} = 19.

Аналогично определяем ∆ (2), ∆ (3), ∆ (4), ∆ (5).

3) Второй шаг. Среди множества подпоследовательностей длиной 1, s1(1) = 1, s2(1) = 2,..., s5(1) = 5 выбираем наиболее перспективную s = 1, для которой величина оценки-прогноза ∆ (s) оказывается наименьшей. Далее развиваем ее, конструируя возможные варианты длиной 2, т. е. (1.2), (1.3), (1.4), (1.5).

Для каждого из этих вариантов вновь определяем оценки по формулам (21) — (24).

Процесс вычислений продолжаем аналогично.

Процесс построения дерева вариантов приведен на рис. 1.

Рисунок 1

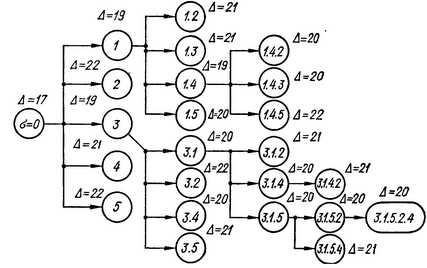
Каждой конечной вершине дерева вариантов будет отвечать полная последовательность s = i1,i2,,.in. Если для некоторой такой вершины величина оценки ∆ (s) не превосходит величины оценок для всех остальных вершин, то эта оценка определяет искомый оптимальный вариант. В противном случае разбиваем более перспективный вариант с наилучшей оценкой.

Конечная вершина определяет вариант (последовательность)  = 3, 1, 5, 2, 4 с наилучшей оценкой ∆ = 20. Поэтому данный вариант является оптимальным.

Непосредственной проверкой убеждаемся, что время обработки всей последовательности деталей для этого варианта совпадает со значением оценки-прогноза и является минимальным:

.

Список литературы

1.  Акулич И.Л. Математическое программирование в примерах и задачах. М., Высшая школа, 1993.

2.  Гончаренко В.М. «Математические методы и модели операций. Руководство к решению задач». М., Финансовая Академия, 2006.

3.  Зайченко Ю.П. Исследование операций. Киев, Высшая школа, 1975.

4.  Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. М., Высшая школа, 1980.

5.  Шкурба В.В. Задача трех станков. М., Наука, 1976.

Приложение 1

Решение задачи

z = 4х1 + х2 +1 ® max  при ограничениях:

 

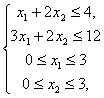
симплекс-методом:

базис	bi	x1	x2	x3	x4	x5	x6
x3	4	1	2	1	0	0	0
x4	12	3	2	0	1	0	0
x5	3	1	0	0	0	1	0
x6	3	0	1	0	1	0	1
z	1	-4	-1	0	0	0	0
x2	2	0,5	1	0,5	0	0	0
x4	8	2	0	-1	1	0	0
x5	3	1	0	0	0	1	0
x6	1	-0,5	0	-0,5	0	0	1
z	3	-3,5	0	1	0	0	0
x1	4	1	2	1	0	0	0
x4	0	0	-2	-2	1	0	0
x5	-1	0	-2	-1	0	1	0
x6	3	0	1	0	0	0	1
z	17	0	7	4,5	0	0	0
x1	3	1	0	0	0	1	0
x4	1	0	0	-1	1	-1	0
X2	0,5	0	1	0,5	0	-0,5	0
x6	2,5	0	0	-0,5	0	0,5	1
z	3,5	0	0	1,5	0	3,5	0

z*=13,5,Х1*=(3;0,5;0;1;0;2,5).

Приложение 2

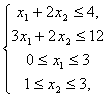
Решение задачи z = 4х1 + х2 +1 ® max при ограничениях:

с помощью табличного процессора Microsoft Excel.

 

Приложение 3

В качестве примера применения метода ветвей и границ приведем поиск оптимального значения функции Z = Зх1 + х2 ® max при ограничениях:

4xl + Зх2 < 18,

x1 + 2x2 £ 6,

0 £ x1 £ 5,

0 £ x2 £ 4,

х1, x2 — целые числа.

Решение

За нижнюю границу линейной функции примем, например, ее значение в точке (0,0), т.е. Z0 = Z (0; 0) = 0.

I этап. Решая задачу симплекс-методом, получим Zmax = 13,5 при Х1* = (4,5; 0; 0; 1,5; 0,5; 4); так как первая компонента х1* дробная, то из области решения исключается полоса, содержащая дробное оптимальное значение х1*, т.е. 4 < х1 < 5. Поэтому задача 1 разбивается на две задачи 2 и 3.

Задача 2

Z=3x1+x2→max

при ограничениях:

4xl + Зх2 < 18

x1 + 2x2 £ 6

0 £ x1 £ 4

0 £ x2 £ 4

 

х1, x2 — целые числа.

Задача 3

Z=3x1+x2→max

при ограничениях:

4xl + Зх2 < 18

x1 + 2x2 £ 6

5 £ x1 £ 5

0 £ x2 £ 4

 

х1, x2 — целые числа.

Список задач: 2 и 3. Нижняя граница линейной функции не изменилась: Z0= 0.

II этап. Решаем (по выбору) одну из задач списка, например задачу 3 симплекс-методом.

Получим, что условия задачи 3 противоречивы.

III этап. Решаем задачу 2 симплекс-методом. Получим Zmax = 12 2/3 при X3*= (4; 2/3; 0; 2/3; 0; 10/3). Хотя Z(X3*) = 12 2/3 > Z0 = 0, по-прежнему сохраняется Z0 = 0, ибо план нецелочисленный. Так как х2* — дробное число, из области решений исключаем полосу 0 < x2 < 1 и задачу 2 разбиваем на две задачи 4 и 5.

Задача 4

Z=3x1+x2→max

при ограничениях:

4xl + Зх2 < 18

x1 + 2x2 £ 6

0 £ x1 £ 4

0 £ x2 £ 0

 

х1, x2 — целые числа.

Задача 5

Z=3x1+x2→max

при ограничениях:

4xl + Зх2 < 18

x1 + 2x2 £ 6

0 £ x1 £ 4

1 £ x2 £ 4

х1, x2 — целые числа.

Список задач: 4 и 5. Значение Z0 = 0.

IV этап. Решаем задачу 4 симплекс-методом.

Получим Zmax = 12 при X4* = (4; 0; 2; 2; 0; 0). Задачу исключаем из списка, но при этом меняем Z0; Z0 = Z(X4*) = 12, ибо план Х4* целочисленный.

V этап. Решаем задачу 5 симплекс-методом.

Получим Zmax = 12,25 при X5* = (3,75; 1; 0; 0,25; 0,25; 0; 3). Z 0 не меняется, т.е. Z0 = 12, ибо план X5* нецелочисленный. Так как х1* — дробное, из области решений исключаем полосу 3<x1<4, и задача 5 разбивается на две задачи: 6 и 7.

Задача 6

Z=3x1+x2→max

при ограничениях:

4xl + Зх2 < 18

x1 + 2x2 £ 6

0 £ x1 £ 3

1 £ x2 £ 4

 

х1, x2 — целые числа.

Задача 7

Z=3x1+x2→max

при ограничениях:

4xl + Зх2 < 18

x1 + 2x2 £ 6

4 £ x1 £ 4

1 £ x2 £ 4

 

х1, x2 — целые числа.

Список задач: 6 и 7. Значение Z0 = 12.

VI этап. Решаем одну из задач списка, например задачу 7, симплекс-методом. Получим, что условия задачи 7 противоречивы.

VII этап. Решаем задачу 6 симплекс-методом. Получим Zmax = 10,5 ,при  X6* = (3; 1,5; 1,5; 0; 0; 0,5; 2,5). Так как, Z(X6*) = 10,5 < Z0 = 12, то задача исключается из списка.

Итак, список задач исчерпан и оптимальным целочисленным решением исходной задачи будет X* = Х4* = (4; 0; 2; 2; 0; 0), а оптимум линейной функции Zmax = 12.

[1] «Оптимальным» будем называть план, оптимальный на данный момент решения.

[2] Естественно, без введения и вычисления переменных искусственного базиса.

[3] «о трех станкак».