Дипломная работа: Спиральные антенны
В практических конструкциях спиральных антенн часто применяется диэлектрик в виде опорных цилиндров, на поверхность которых укладываются заходы. Если диэлектрик однороден в азимутальном и продольном направлениях, то свойства симметрии спиральной структуры не изменяются.
Для уменьшения поперечных размеров спиральной антенны можно использовать замедляющие системы, уменьшающие фазовую скорость тока в заходах спирали. Такая замедляющая система может быть однородной в азимутальном и продольном направлениях. Кроме того, проводник спирали может представлять собой замедляющую систему (например, спираль малого радиуса или зигзагообразную ленту), причем однородную вдоль спирального направления. В этих случаях свойства симметрии структуры также не изменяются. В дальнейшем предполагается, что и диэлектрик, и замедляющие системы не нарушают свойств симметрии.
Рассмотрим свойства полей в системах с различной симметрией.
Пусть рассматриваемая система имеет поворотную ось симметрии См, т.е. представляет собой М-заходную произвольную спираль — плоскую, коническую или цилиндрическую.
Как показано, поле произвольным образом возбужденной замедляющей системы с поворотной осью симметрии См можно представить в виде суммы М так называемых нормальных волн, каждая из которых удовлетворяет граничным условиям в системе. Вектор напряженности электрического поля в q-й нормальной волне может быть записан в виде
Eq (r, φ, z) =Е0q(r, φ, z)ехр[-ίqφ],(4.1.1)
где q- целое число, характеризующее тип волны,
-М/2<q≤Μ/2; Е0q — периодическая функция координаты φ цилиндрической системы координат, ось z которой совпадает с осью симметрии См. Период функции равен 2π/M и ее можно разложить в ряд Фурье:
Еоq(r,φ,z)=
emq(r,z)exp[-imMφ] (4.1.2)
е — коэффициент разложения. Из (4.1.1) и (4.1.2) cледует выражение для поля q-й нормальной волны:
Eq(r,φ,z)=
emq(r,z)exp[-ίνφ], (4.1.3)
где ν=qmΜ. (4.1.4)
Выражение (1.3) представляет собой разложение поля этой нормальной волны на так называемые азимутальные пространственные гармоники.
Аналогично можно представить токи в системе, соответствующие q-й нормальной волне:
jq(r,φ,z)=
jmq(r,z) exp[-ίνφ]. (4.1.5)
Из (1.3) — (1.5) следует, что в q-ю нормальную волнy входят азимутальные пространственные гармоники с индексами ν=q+mM .
Поля и токи в соседних симметричных точках (в точках, совмещающихся при повороте системы вокруг оси| z на угол 2π/М) связаны соотношениями:
Еq (r, φ + 2π/М, z) = Еq (r,φ,z ) exp [-ί2πq/Μ]; (4.1.6)
jq (r,φ+2π/M, z) = jq (r,φ, z) exp [— ί2πq/M].
Из (4.2.6) следует, что поля и токи в указанных точках одинаковы по амплитуде и сдвинуты по фазе на 2πq/M. Если возбуждающие заходы спирали э. д. с. (или токи) одинаковы по амплитуде и сдвинуты по фазе на указанную величину, в системе возбуждается только q-я нормальная волна. В этой волне при заданных геометрических размерах спирали в зависимости от частоты может резонировать та или другая азимутальная пространственная гармоника, входящая в возбуждаемую нормальную волну. Резонирующая пространственная гармоника даст основной вклад в поле излучения и определяет диаграмму направленности, поляризационную и фазовую характеристики всей антенны в дальней зоне.
Аналогично поле произвольно возбужденной системы с винтовой осью симметрии СM1 также можно представить в виде суммы М нормальных волн, удовлетворяющих граничным условиям:
E(r, φ,
z)=
Eq (r,φ,z),
где для четных М
q1=1-Μ/2, q2= М/2,(4.1.7)
для нечетных М
q1=(1-M)/2, q2=(M-1)/2;
Eq(r, φ, z) = E0q(r, φ, z)ехр[-ί(β+ 2πq/S)z]. (4.1.8)
Функция E0q(r, φ, z) удовлетворяет условиям:
Е0q(r, φ, z)=E0q(r, φ, z + S/M), (4.1.9)
Е0q(r, φ+2π/Μ, z) = E0q(r, φ, z)exp[—ί2πq/M] (4.1.10)
и имеет периоды по z и φ соответственно S/M и 2π.
Разложив E0q(r, φ, z) в ряды Фурье по z и φ, получим
Е0q (r, φ, z)= 
et νq(r)exp[-ί2πΜtz/S]exp[-ίνφ] (4.1.11)
Из (1.10) и (1.11), приравнивая показатели экспонент, получаем следующее соотношение:
νφ+2πν/M=νφ+2πq/Μ+2πm, m=0, ±1, ±2, ..., (4.1.12)
отсюда ν=q+mM.
Из (4.1.8), (4.1.11) и (4.1.12) следует выражение для поля q-й нормальной волны:
Еq (r, φ, z)= 
enνq(r)exp[-ίβnz-ίνφ], (4.1.13)
βn=β+2πn/S, n=q+tM (4.1.14)
В аналогичном виде записывается выражение плотности тока проводимости, текущего в заходах спирали, соответствующего q-й нормальной волне:
jq(r, φ, z)=
jn νq(r)exp[-ίβnz-ίνφ].
Выражение (4.1.13) представляет собой разложение вектора напряженности электрического поля q-й нормальной волны в ряд по азимутальным и так называемым продольным пространственным гармоникам, именуемым также φ- и z- гармониками .
Как следует из (4.1.12) и (4.1.14), спектры азимутальных и продольных пространственных гармоник в нормальной волне разрежены тем более, чем больше число заходов спирали М.
Если э.д.с. (или токи),
возбуждающие заходы спирали, одинаковы по амплитуде и сдвинуты по фазе в
соседних заходах на 2πq/М, то q-я нормальная волна
возбуждается в чистом виде. В зависимости от отношения диаметра спирали и длины
волны колебаний в q-й нормальной
волне может резонировать та или иная азимутальная и продольная пространственные
гармоники. Индекс резонирующей азимутальной пространственной гармоники и
определяет характер излучения спиральной антенны (диаграммы направленности,
поляризационные, фазовые характеристики и т. д.). В системах с однородным
диэлектриком продольные пространственные гармоники в областях пространственного
резонанса замедлены очень слабо и имеют фазовую скорость, близкую к ±1
0
(ε—диэлектрическая проницаемость диэлектрика, в котором расположена
спиральная система).
Значительное преобладание резонирующей пространственной гармоники над всеми другими позволяет в приближенных расчетах (и тем более при качественном анализе) характеристик спиральной антенны учитывать только резонирующую гармонику. Отбрасывание нерезонансных пространственных гармоник эквивалентно замене спирали на анизотропно проводящую модель.
Такая модель представляет собой плоскую, коническую или цилиндрическую поверхность, на которой имеется не М реально существующих заходов, а бесконечное множество проводящих нитей, расположенных на бесконечно малом расстоянии друг от друга, т. е. поверхность, проводящую только в спиральном направлении и не проводящую в перпендикулярном ему направлении. В анизотропно проводящей модели, как следует из выражения (4.1.12), в каждую нормальную волну (а количество их возрастает до бесконечности) входит лишь q-я азимутальная пространственная гармоника. Указанная замена существенно упрощает расчет и особенно качественный анализ характеристик излучения различных нормальных волн — диаграмм направленности, поляризационных и фазовых характеристик.
Характеристики излучения нормальных волн.
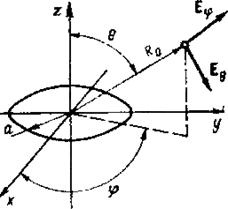
Рис 4.1.1. К определению поля кольца с бегущей волной тока.
При анализе поля излучения анизотропно проводящей модели спиральной антенны ее комплексную диаграмму направленности f˙(θ) можно представить в виде произведения комплексных диаграмм направленности элемента f˙(θ) и множителя системы f˙c(θ).
Поскольку в анизотропно проводящей модели по координате φ укладывается целое число периодов изменения поля и тока, в качестве элемента такой модели необходимо взять азимутальное кольцо с бегущей волной тока. На длине кольца должно укладываться целое число длин волн. Для кольца радиуса α, на длине которого укладывается ν длин волн, нетрудно получить следующие выражения для комплексных диаграмм направленности по θ-й и φ-й компонентам (рис. 4.1.1):
f˙1θ(θ)=-ίexp[-ίκR0-ίκR0-ίνφ][J(ν-1)(καsinθ)+J(ν+1)(καsinθ)]cosθ, (4.1.15)
f˙1φ(θ)=exp[-ίκR0-ίνφ][J(ν-1)(καsinθ)-J(ν+1)(καsinθ)]. (4.1.16)
где κ=2π/λ, λ – длина волны в свободном пространстве, J(ν±1) - функция Бесселя действительного аргумента.
Рассчитанные по формулам (4.1.15) и (4.1.16) диаграммы направленности для различных азимутальных гармоник при κα=ν - показаны на рис. 4.1.1.
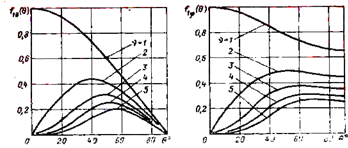
Рис.4.1.2. Диаграммы направленности азимутальных пространственных гармоник.
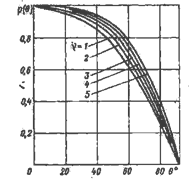
Рис.4.1.3. Поляризационные характеристики азимутальных пространственных гармоник.
Ранее отмечалось, что в областях резонанса пространственных гармоник фазовая скорость близка к значению ±с, поэтому множитель системы fc(θ) имеет главный максимум направлении оси симметрии (в направлении θ=0, π). Излучение главным максимумом направлении θ=0 называется прямым осевым в направлении θ=π - обратным осевым. В первом случае направление главного максимума диаграммы направленности и направление осевой составляющей υф волны тока в проводе спирали совпадают, во втором случае противоположны. Для плоских спиралей практически fc(θ)≈1. Для цилиндрических регулярных спиралей множитель системы приближенно может быть рассчитан по формуле, получение для антенны бегущей волны:
fc(θ) ≈ (sinψ/ψ) e-ίψ, (4.1.17)
где ψ ≈ (1-cosθ) κLz/2 – фаза на сфере, описанной относительно начала спирали; Lz – длина спирали вдоль ее оси.
Формулой (4.1.17) можно пользоваться для грубой оценки множителя системы и коническойспирали. В этом случае Lz – осевая длина зоны, в пределах которой интенсивно излучается рассматриваемая резонирующая гармоника.
Из (4.1.15) и (4.1.16) следует выражение для поляризационной характеристики ν-й пространственной гармоники (зависимости коэффициента поляризации р от угла θ):
P(θ)≈
(4.1.18)
Зависимость р(θ) для различных гармоник показана на рис. 4.1.4.
Рис.4.1.4. Точка возбуждения многозаходной спиральной антенны.
Зависимость фазы в дальней зоне от углов θ, φ (фазовая характеристика) в соответствии с выражениями (4.1.15), (4.1.16) и (4.1.17) в плоскости φ = const определяется функцией ψ(θ), а на поверхности θ = const — функцией νφ.
Из выражений (4.1.15) — (4.1.18) и приведенных графиков следует, что режим прямого (или обратного) осевого излучения обусловлен излучением первой азимутальной пространственнойгармоники (ν=±l). Причем при ν=l поляризация в направлении оси — правая круговая, при ν= — 1 — левая круговая. Все другие пространственные гармоники не обеспечивают режима осевого излучения.
Если гармоники с ν=±l имеют одинаковые амплитуды, поле в направлении оси спирали поляризовано линейно. Очевидно, получение чисто круговой поляризации возможно в том случае, когда возбуждение гармоники с ν=l (или ν= — 1) исключает возбуждение гармоники с ν=- 1 (или ν=l). С этой точки зрения, в одно- и двухзаходных спиралях в принципе невозможно получить круговую поляризацию в направлении оси, так как гармоники с ν=±l входят в одну и ту же нормальную волну. При М>2 гармоники с ν=±l входят, как это следует из (4.1.12), в нормальные волны с q1= 1 и q2= М—1, не связанные между собой граничными условиями. Поэтому в таких антеннах поляризация поля излучения в направлении оси z (оси спирали) может быть круговой правой при возбуждении симметричных точек токами
Ј1+=J1+exp[ ί2πq1( l-1)/M]= Ј1+exp[ί2π(l-1)/M] (4.1.19)
и круговой левой при возбуждении симметричных точек токами
Ј1-=J1-exp[ ί2πq2( l-1)/M]= Ј1-exp[ί2π(l-1)/M] (4.1.20)
В спирали с односторонней намоткой при Ј1+= Ј1- амплитуды гармоник с ν=±l различны. Так, в спирали с правовинтовой намоткой заходов амплитуда гармоники с ν=l существенно превышает амплитуду гармоники с ν = — 1; в спирали с левовинтовой намоткой заходов — наоборот. Вследствие этого в таких спиралях управление поляризацией излучения невозможно.
Если из каждой симметричной точки начинаются симметрично правый и левый заходы, то при Ј1+= Ј1- амплитуды гармоник с ν = ± 1 будут одинаковыми. В такой спирали, называемой ниже спиралью с двусторонней намоткой, возможно управление поляризацией излучения, если М>2. В частности, в направлении оси z поляризация линейна при Ј1+= Ј1-, правая эллиптическая - при Ј1+> Ј1-, левая эллиптическая - при Ј1+< Ј1-, круговая— при Ј1+=0 (Ј1- =0).
4.2 Расчет диаграммы направленности плоской спиральной антенны
Диаграммы направленности плоских спиральных антенн могут быть рассчитаны по следующим формулам:
, (4.2.1)
, (4.2.2)
где 
- электрический
периметр активной области рабочей волны Тn; Jn(x), J'n(x)—функция Бесселя n-го порядка и ее производная по
аргументу.
Произведем расчет диаграмм направленности по формулам (4.2.1),(4.2.2), при ка=1,5; ка=2; ка=3; ка=3,5.
При расчете используется приложение Mathcad 12.
Расчеты диаграмм направленности сведены в таблицы 1 и 2.
По расчётам построены диаграммы направленности рис.(4.2.1-4.2.9)
Выводы
Для расчета характеристик и параметров спиральной антенны мы использовали знание фазовой скорости волны тока распространяющейся вдоль спирали; только зная эту величину мы произвели расчет характеристик направленности, коэффициента направленного действия, фазовых характеристик, поляризационных характеристик и входного сопротивления СА.
антенна спираль волна сотовый телефон
Литература
